|
Flux
Flux describes any effect that appears to pass or travel (whether it actually moves or not) through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications in physics. For transport phenomena, flux is a vector quantity, describing the magnitude and direction of the flow of a substance or property. In vector calculus flux is a scalar quantity, defined as the surface integral of the perpendicular component of a vector field over a surface. Terminology The word ''flux'' comes from Latin: ''fluxus'' means "flow", and ''fluere'' is "to flow". As '' fluxion'', this term was introduced into differential calculus by Isaac Newton. The concept of heat flux was a key contribution of Joseph Fourier, in the analysis of heat transfer phenomena. His seminal treatise ''Théorie analytique de la chaleur'' (''The Analytical Theory of Heat''), defines ''fluxion'' as a central quantity and proceeds to derive the now well-known expre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Flux
In physics, specifically electromagnetism, the magnetic flux through a surface is the surface integral of the normal component of the magnetic field B over that surface. It is usually denoted or . The SI unit of magnetic flux is the weber (Wb; in derived units, volt–seconds or V⋅s), and the CGS unit is the maxwell. Magnetic flux is usually measured with a fluxmeter, which contains measuring coils, and it calculates the magnetic flux from the change of voltage on the coils. Description The magnetic interaction is described in terms of a vector field, where each point in space is associated with a vector that determines what force a moving charge would experience at that point (see Lorentz force). Since a vector field is quite difficult to visualize, introductory physics instruction often uses field lines to visualize this field. The magnetic flux, through some surface, in this simplified picture, is proportional to the number of field lines passing through that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
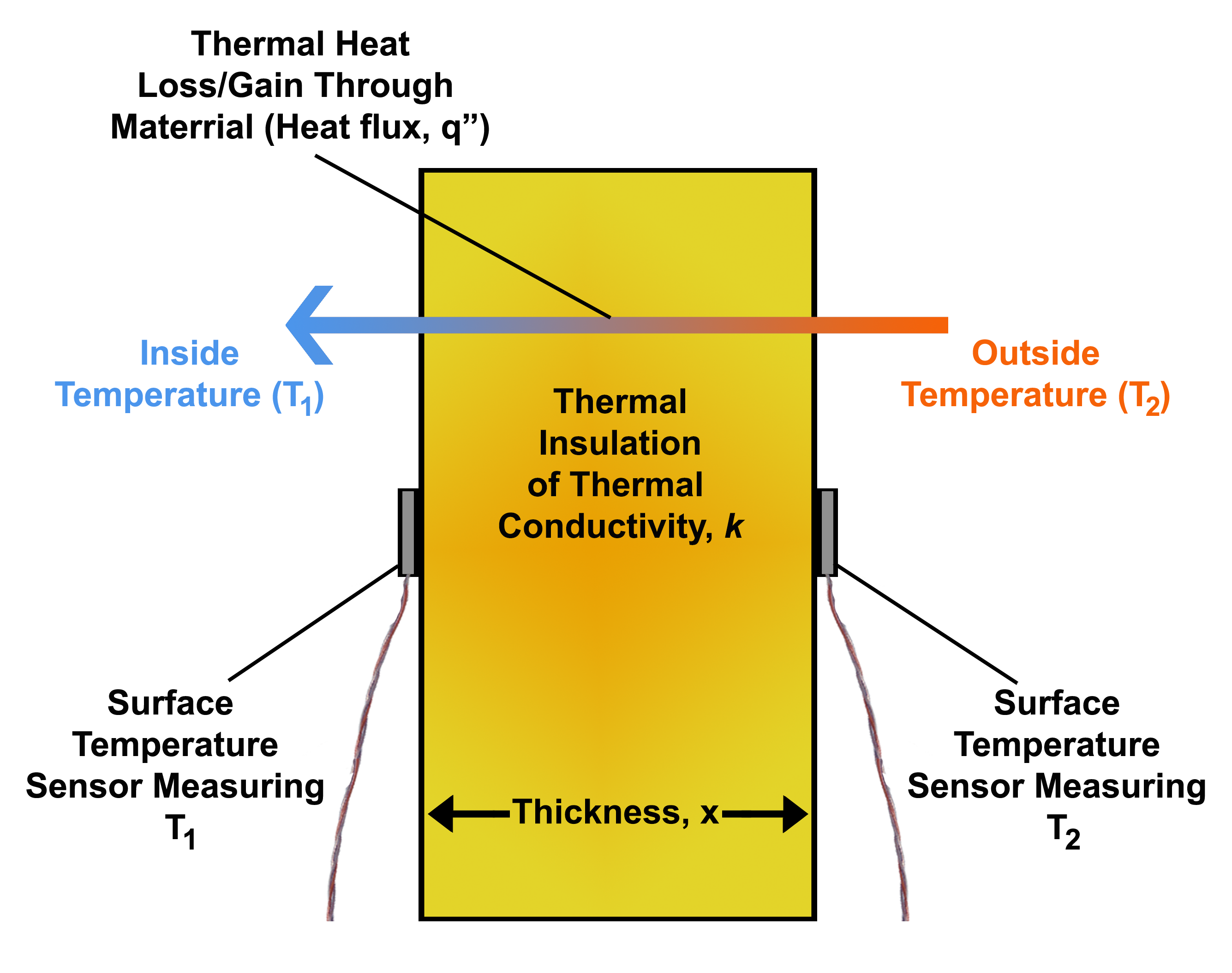
Heat Flux
In physics and engineering, heat flux or thermal flux, sometimes also referred to as heat flux density, heat-flow density or heat-flow rate intensity, is a flow of energy per unit area per unit time (physics), time. Its SI units are watts per square metre (W/m2). It has both a direction and a magnitude, and so it is a Vector (geometric), vector quantity. To define the heat flux at a certain point in space, one takes the Limiting case (mathematics), limiting case where the size of the surface becomes infinitesimally small. Heat flux is often denoted \vec_\mathrm, the subscript specifying ''heat'' flux, as opposed to ''Mass flux, mass'' or Transport phenomena, ''momentum'' flux. Heat conduction#Fourier's law, Fourier's law is an important application of these concepts. Fourier's law For most solids in usual conditions, heat is transported mainly by thermal conduction, conduction and the heat flux is adequately described by Fourier's law. Fourier's law in one dimension \phi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Transfer
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, Convection (heat transfer), thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species (mass transfer in the form of advection), either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system. Heat conduction, also called diffusion, is the direct microscopic exchanges of kinetic energy of particles (such as molecules) or quasiparticles (such as lattice waves) through the boundary between two systems. When an object is at a different temperature from another body or its surroundings, heat flows so that the body and the surroundings reach the same temperature, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, one may integrate over this surface a scalar field (that is, a function of position which returns a scalar as a value), or a vector field (that is, a function which returns a vector as value). If a region R is not flat, then it is called a ''surface'' as shown in the illustration. Surface integrals have applications in physics, particularly in the classical theories of electromagnetism and fluid mechanics. Surface integrals of scalar fields Assume that ''f'' is a scalar, vector, or tensor field defined on a surface ''S''. To find an explicit formula for the surface integral of ''f'' over ''S'', we need to parameterize ''S'' by defining a system of curvilinear coordinates on ''S'', like the latitude and longitude on a sphere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transport Phenomena
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others. The fundamental analysis in all three subfields of mass, heat, and momentum transfer are often grounded in the simple principle that the total sum of the quantities being studied must be conserved by the system and its environment. Thus, the different phenomena that lead to transport are each considered individually with the knowled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Quantity
A physical quantity (or simply quantity) is a property of a material or system that can be Quantification (science), quantified by measurement. A physical quantity can be expressed as a ''value'', which is the algebraic multiplication of a ''numerical value'' and a ''unit of measurement''. For example, the physical quantity mass, symbol ''m'', can be quantified as ''m'n''kg, where ''n'' is the numerical value and kg is the unit symbol (for kilogram). Quantities that are vectors have, besides numerical value and unit, direction or orientation in space. Components Following ISO 80000-1, any value or Magnitude (mathematics), magnitude of a physical quantity is expressed as a comparison to a unit of that quantity. The ''value'' of a physical quantity ''Z'' is expressed as the product of a ''numerical value'' (a pure number) and a unit [''Z'']: :Z = \ \times [Z] For example, let Z be "2 metres"; then, \ = 2 is the numerical value and [Z] = \mathrm is the unit. Conversely, the nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Method Of Fluxions
''Method of Fluxions'' () is a mathematical treatise by Sir Isaac Newton which served as the earliest written formulation of modern calculus. The book was completed in 1671 and posthumously published in 1736. Background Fluxion is Newton's term for a derivative. He originally developed the method at Woolsthorpe Manor during the closing of Cambridge due to the Great Plague of London from 1665 to 1667. Newton did not choose to make his findings known (similarly, his findings which eventually became the '' Philosophiae Naturalis Principia Mathematica'' were developed at this time and hidden from the world in Newton's notes for many years). Gottfried Leibniz developed his form of calculus independently around 1673, seven years after Newton had developed the basis for differential calculus, as seen in surviving documents like “the method of fluxions and fluents..." from 1666. Leibniz, however, published his discovery of differential calculus in 1684, nine years before Newton forma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, achieved the Unification of theories in physics#Unification of gravity and astronomy, first great unification in physics and established classical mechanics. Newton also made seminal contributions to optics, and Leibniz–Newton calculus controversy, shares credit with German mathematician Gottfried Wilhelm Leibniz for formulating calculus, infinitesimal calculus, though he developed calculus years before Leibniz. Newton contributed to and refined the scientific method, and his work is considered the most influential in bringing forth modern science. In the , Newton formulated the Newton's laws of motion, laws of motion and Newton's law of universal g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Calculus
Vector calculus or vector analysis is a branch of mathematics concerned with the differentiation and integration of vector fields, primarily in three-dimensional Euclidean space, \mathbb^3. The term ''vector calculus'' is sometimes used as a synonym for the broader subject of multivariable calculus, which spans vector calculus as well as partial differentiation and multiple integration. Vector calculus plays an important role in differential geometry and in the study of partial differential equations. It is used extensively in physics and engineering, especially in the description of electromagnetic fields, gravitational fields, and fluid flow. Vector calculus was developed from the theory of quaternions by J. Willard Gibbs and Oliver Heaviside near the end of the 19th century, and most of the notation and terminology was established by Gibbs and Edwin Bidwell Wilson in their 1901 book, '' Vector Analysis'', though earlier mathematicians such as Isaac Newton pioneered ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Area
In 3-dimensional geometry and vector calculus, an area vector is a vector combining an area quantity with a direction, thus representing an oriented area in three dimensions. Every bounded surface in three dimensions can be associated with a unique area vector called its vector area. It is equal to the surface integral of the surface normal, and distinct from the usual ( scalar) surface area. Vector area can be seen as the three dimensional generalization of signed area in two dimensions. Definition For a finite planar surface of scalar area and unit normal , the vector area is defined as the unit normal scaled by the area: \mathbf = \hat \mathbfS For an orientable surface composed of a set of flat facet areas, the vector area of the surface is given by \mathbf = \sum_i \hat \mathbf_i S_i where is the unit normal vector to the area . For bounded, oriented curved surfaces that are sufficiently well-behaved, we can still define vector area. First, we split the su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale Geophysical fluid dynamics, geophysical flows involving oceans/atmosphere and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish physicist and mathematician who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism and light as different manifestations of the same phenomenon. Maxwell's equations for electromagnetism achieved the Unification (physics)#Unification of magnetism, electricity, light and related radiation, second great unification in physics, where Unification (physics)#Unification of gravity and astronomy, the first one had been realised by Isaac Newton. Maxwell was also key in the creation of statistical mechanics. With the publication of "A Dynamical Theory of the Electromagnetic Field" in 1865, Maxwell demonstrated that electric force, electric and magnetic fields travel through space as waves moving at the speed of light. He proposed that light is an undulation in the same medium that is the cause of electric and magnetic phenomena. (Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |