|
Flexural Modulus
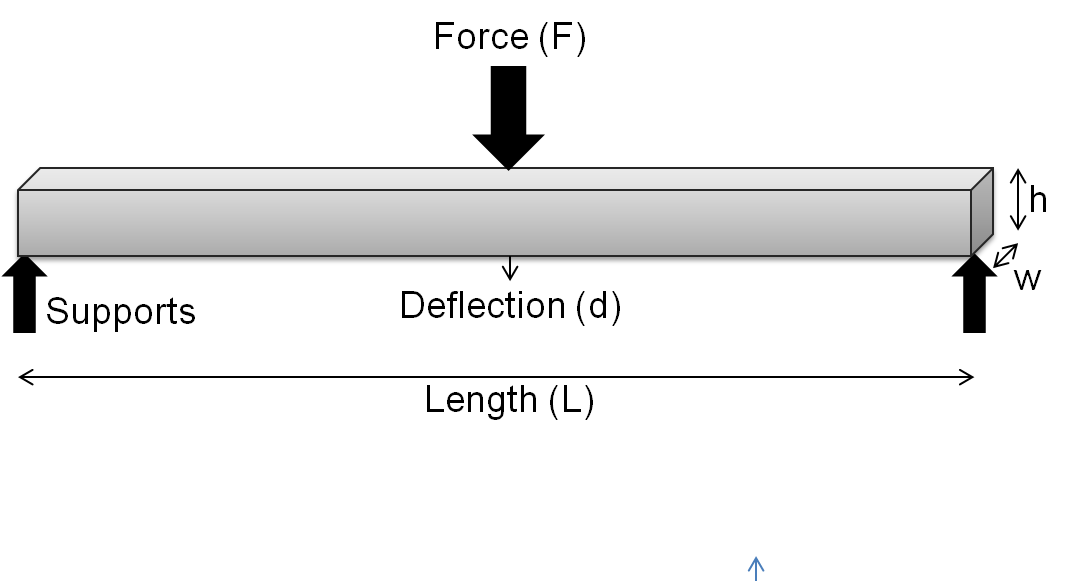
In mechanics, the flexural modulus, bending modulus, or modulus of rigidity is an intensive property that is computed as the ratio of stress to strain in flexural deformation, or the tendency for a material to resist bending. It is determined from the slope of a stress-strain curve produced by a flexural test (such as the ASTM D790), and uses units of force per area. The flexural modulus defined using the 2-point (cantilever) and 3-point bend tests assumes a linear stress strain response. For a 3-point test of a rectangular beam behaving as an isotropic linear material, where ''w'' and ''h'' are the width and height of the beam, ''I'' is the second moment of area of the beam's cross-section, ''L'' is the distance between the two outer supports, and ''d'' is the deflection due to the load ''F'' applied at the middle of the beam, the flexural modulus: : E_ = \frac From elastic beam theory :d = \frac and for rectangular beam : I = \fracwh^3 thus E_ = E (Elastic modulus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanics
Mechanics () is the area of physics concerned with the relationships between force, matter, and motion among Physical object, physical objects. Forces applied to objects may result in Displacement (vector), displacements, which are changes of an object's position relative to its environment. Theoretical expositions of this branch of physics has its origins in Ancient Greece, for instance, in the writings of Aristotle and Archimedes (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo Galilei, Johannes Kepler, Christiaan Huygens, and Isaac Newton laid the foundation for what is now known as classical mechanics. As a branch of classical physics, mechanics deals with bodies that are either at rest or are moving with velocities significantly less than the speed of light. It can also be defined as the physical science that deals with the motion of and forces on bodies not in the quantum realm. History ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intensive Property
Physical or chemical properties of materials and systems can often be categorized as being either intensive or extensive, according to how the property changes when the size (or extent) of the system changes. The terms "intensive and extensive quantities" were introduced into physics by German mathematician Georg Helm in 1898, and by American physicist and chemist Richard C. Tolman in 1917. According to International Union of Pure and Applied Chemistry (IUPAC), an intensive property or intensive quantity is one whose magnitude is independent of the size of the system. An intensive property is not necessarily homogeneously distributed in space; it can vary from place to place in a body of matter and radiation. Examples of intensive properties include temperature, ''T''; refractive index, ''n''; density, ''ρ''; and hardness, ''η''. By contrast, an extensive property or extensive quantity is one whose magnitude is additive for subsystems. Examples include mass, volume and Gi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (physics)
In continuum mechanics, stress is a physical quantity that describes Force, forces present during Deformation (physics), deformation. For example, an object being pulled apart, such as a stretched elastic band, is subject to Tension (physics), ''tensile'' stress and may undergo Elongation (materials science), elongation. An object being pushed together, such as a crumpled sponge, is subject to Compression (physics), ''compressive'' stress and may undergo shortening. The greater the force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Stress has Dimension (physics), dimension of force per area, with SI Units, SI units of newtons per square meter (N/m2) or Pascal (unit), pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while Strain (mechanics), ''strain'' is the measure of the relative deformation (mechanics), deformation of the material. For example, when a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strain (materials Science)
In mechanics, strain is defined as relative deformation, compared to a position configuration. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered. Strain has dimension of a length ratio, with SI base units of meter per meter (m/m). Hence strains are dimensionless and are usually expressed as a decimal fraction or a percentage. Parts-per notation is also used, e.g., parts per million or parts per billion (sometimes called "microstrains" and "nanostrains", respectively), corresponding to μm/m and nm/m. Strain can be formulated as the spatial derivative of displacement: \boldsymbol \doteq \cfrac\left(\mathbf - \mathbf\right) = \boldsymbol'- \boldsymbol, where is the identity tensor. The displacement of a body may be expressed in the form , where is the reference position of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexural Strength
Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the Stress (mechanics), stress in a material just before it Yield (engineering), yields in a flexure test. The transverse bending test is most frequently employed, in which a specimen having either a circular or rectangular cross-section is bent until fracture or yielding using a three-point flexural test technique. The flexural strength represents the highest stress experienced within the material at its moment of yield. It is measured in terms of stress, here given the symbol \sigma. Introduction When an object is formed of a single material, like a wooden beam or a steel rod, is bent (Fig. 1), it experiences a range of stresses across its depth (Fig. 2). At the edge of the object on the inside of the bend (concave face) the stress will be at its maximum compressive stress value. At the outside of the bend (convex face) the stress will b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ASTM
ASTM International, formerly known as American Society for Testing and Materials, is a standards organization that develops and publishes voluntary consensus technical international standards for a wide range of materials, products, systems and services. Some 12,575 apply globally. The headquarters is in West Conshohocken, Pennsylvania, about northwest of Philadelphia. It was founded in 1902 as the American Section of the International Association for Testing Materials. In addition to its traditional standards work, ASTM operates several global initiatives advancing additive manufacturing, advanced manufacturing, and emerging technologies, including the Additive Manufacturing Center of Excellence (AM CoE), the acquisition oWohlers Associatesfor market intelligence and advisory services, and the NIST-funded Standardization Center of Excellence (SCOE). History In 1898, a group of scientists and engineers, led by chemist, industry leader, and proponent of standardization Ch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Moment Of Area
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an I (for an axis that lies in the plane of the area) or with a J (for an axis perpendicular to the plane). In both cases, it is calculated with a multiple integral over the object in question. Its dimension is L (length) to the fourth power. Its unit of dimension, when working with the International System of Units, is meters to the fourth power, m4, or inches to the fourth power, in4, when working in the Imperial System of Units or the US customary system. In structural engineering, the second moment of area of a beam is an important property used in the calculation of the beam's deflection and the calculation of stress caused by a moment applied to the beam. In order to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. Definition The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus. An elastic modulus has the form: :\delta \ \stackrel\ \frac where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. Since strain is a dimensionless quantity, the units of \delta will be the same as the units of stress. Elastic constants and moduli Elastic constants are specific parameters that quantify the stiffness of a material in response to applied stresses and are fundamental in defining the elastic pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropy
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modulus Of Elasticity
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. Definition The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus. An elastic modulus has the form: :\delta \ \stackrel\ \frac where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. Since strain is a dimensionless quantity, the units of \delta will be the same as the units of stress. Elastic constants and moduli Elastic constants are specific parameters that quantify the stiffness of a material in response to applied stresses and are fundamental in defining the elastic pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Young's Modulus
Young's modulus (or the Young modulus) is a mechanical property of solid materials that measures the tensile or compressive stiffness when the force is applied lengthwise. It is the modulus of elasticity for tension or axial compression. Young's modulus is defined as the ratio of the stress (force per unit area) applied to the object and the resulting axial strain (displacement or deformation) in the linear elastic region of the material. Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The first experiments that used the concept of Young's modulus in its modern form were performed by the Italian scientist Giordano Riccati in 1782, pre-dating Young's work by 25 years. The term modulus is derived from the Latin root term '' modus'', which means ''measure''. Definition Young's modulus, E, quantifies the relationship between tensile or compressive stress \sigma (force per unit ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |