|
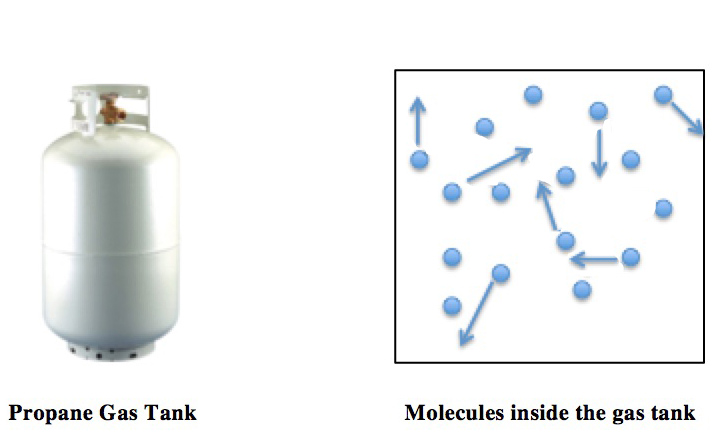
Equipartition
In classical statistical mechanics, the equipartition theorem relates the temperature of a system to its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among all of its various forms; for example, the average kinetic energy per degree of freedom in translational motion of a molecule should equal that in rotational motion. The equipartition theorem makes quantitative predictions. Like the virial theorem, it gives the total average kinetic and potential energies for a system at a given temperature, from which the system's heat capacity can be computed. However, equipartition also gives the average values of individual components of the energy, such as the kinetic energy of a particular particle or the potential energy of a single spring. For example, it predicts that every atom in a monatomic i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making up a substance. Thermometers are calibrated in various temperature scales that historically have relied on various reference points and thermometric substances for definition. The most common scales are the Celsius scale with the unit symbol °C (formerly called ''centigrade''), the Fahrenheit scale (°F), and the Kelvin scale (K), with the third being used predominantly for scientific purposes. The kelvin is one of the seven base units in the International System of Units (SI). Absolute zero, i.e., zero kelvin or −273.15 °C, is the lowest point in the thermodynamic temperature scale. Experimentally, it can be approached very closely but not actually reached, as recognized in the third law of thermodynamics. It would be impossible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion. Thermodynamic temperature is typically expressed using the Kelvin scale, where the unit of measurement is the ''kelvin'' (unit symbol: K). The Kelvin scale uses the same degree interval as the Celsius scale but is offset so that 0 K corresponds to absolute zero. For comparison, a temperature of 295 K corresponds to 21.85 °C and 71.33 °F. Another absolute scale of temperature is the Rankine scale, which is based on the Fahrenheit degree interval. Historically, thermodynamic temperature was defined by Lord Kelvin in terms of a macroscopic relation between Work (thermodynamics), thermodynamic work and Heat, heat transfer as defined in thermodynamics, but the kelvin was redefined by international agreement in 2019 in terms of phenomena that are now understood as man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the molar gas constant, in Planck's law of black-body radiation and Boltzmann's entropy formula, and is used in calculating Johnson–Nyquist noise, thermal noise in resistors. The Boltzmann constant has Dimensional analysis, dimensions of energy divided by temperature, the same as entropy and heat capacity. It is named after the Austrian scientist Ludwig Boltzmann. As part of the 2019 revision of the SI, the Boltzmann constant is one of the seven "Physical constant, defining constants" that have been defined so as to have exact finite decimal values in SI units. They are used in various combinations to define the seven SI base units. The Boltzmann constant is defined to be exactly joules per kelvin, with the effect of defining the SI unit ke ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
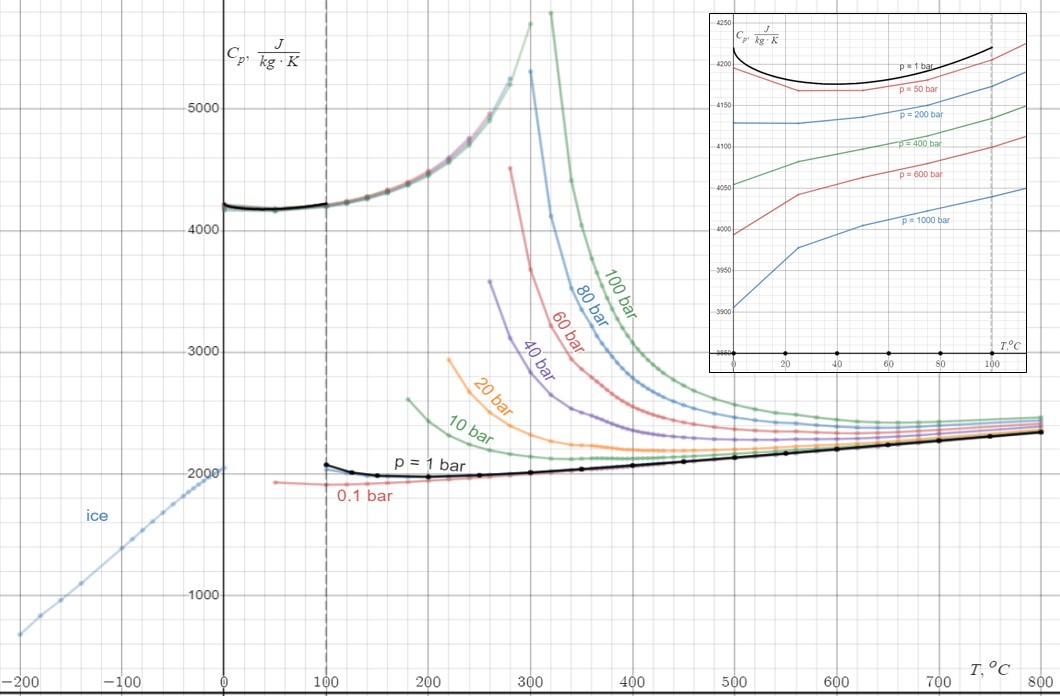
Specific Heat Capacity
In thermodynamics, the specific heat capacity (symbol ) of a substance is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. It is also referred to as massic heat capacity or as the specific heat. More formally it is the heat capacity of a sample of the substance divided by the mass of the sample. The SI unit of specific heat capacity is joule per kelvin per kilogram, J⋅kg−1⋅K−1. For example, the heat required to raise the temperature of of water by is , so the specific heat capacity of water is . Specific heat capacity often varies with temperature, and is different for each state of matter. Liquid water has one of the highest specific heat capacities among common substances, about at 20 °C; but that of ice, just below 0 °C, is only . The specific heat capacities of iron, granite, and hydrogen gas are about 449 J⋅kg−1⋅K−1, 790 J⋅kg−1⋅K−1, and 143 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virial Theorem
In mechanics, the virial theorem provides a general equation that relates the average over time of the total kinetic energy of a stable system of discrete particles, bound by a conservative force (where the work done is independent of path), with that of the total potential energy of the system. Mathematically, the theorem states that \langle T \rangle = -\frac12\,\sum_^N \langle\mathbf_k \cdot \mathbf_k\rangle, where T is the total kinetic energy of the N particles, F_k represents the force on the kth particle, which is located at position , and angle brackets represent the average over time of the enclosed quantity. The word virial for the right-hand side of the equation derives from , the Latin word for "force" or "energy", and was given its technical definition by Rudolf Clausius in 1870. The significance of the virial theorem is that it allows the average total kinetic energy to be calculated even for very complicated systems that defy an exact solution, such as those co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom (physics And Chemistry)
In physics and chemistry, a degree of freedom is an independent physical parameter in the chosen parameterization of a physical system. More formally, given a parameterization of a physical system, the number of degrees of freedom is the smallest number n of parameters whose values need to be known in order to always be possible to determine the values of ''all'' parameters in the chosen parameterization. In this case, any set of n such parameters are called degrees of freedom. The location of a particle in three-dimensional space requires three Coordinate system, position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. So, if the time evolution of the system is Deterministic system, deterministic (where the state at one instant uniquely determines its past and future position and velocity as a function of time), such a system has six degrees of f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and Thermodynamic temperature, temperature respectively; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory of gases, kinetic theory, as was achieved (independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state function, state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
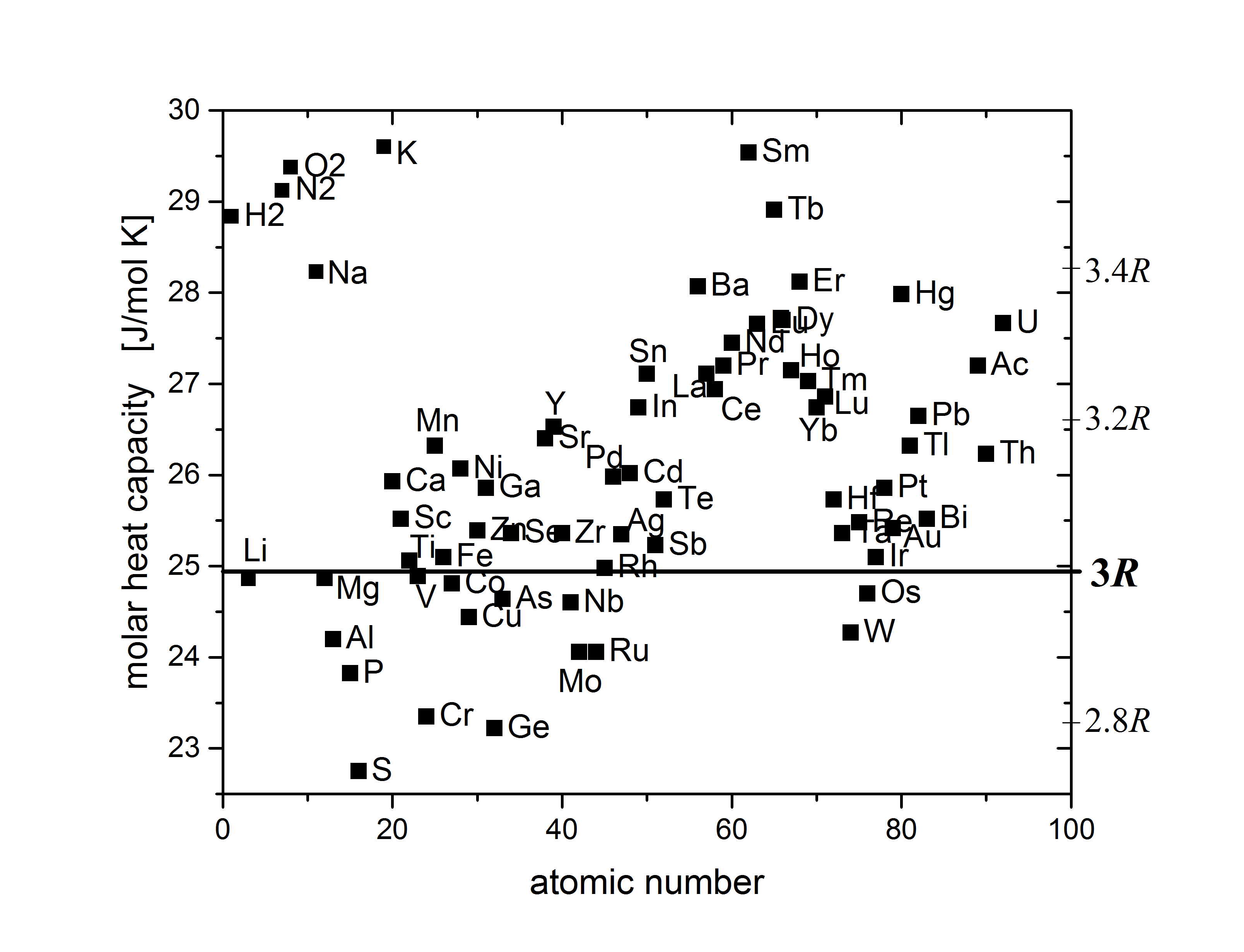
Dulong–Petit Law
The Dulong–Petit law, a thermodynamic law proposed by French physicists Pierre Louis Dulong and Alexis Thérèse Petit, states that the classical expression for the molar specific heat capacity of certain chemical elements is constant for temperatures far from the absolute zero. In modern terms, Dulong and Petit found that the heat capacity of a mole (unit), mole of many solid elements is about 3''R'', where ''R'' is the universal gas constant. The modern theory of the heat capacity of solids states that it is due to phonon, lattice vibrations in the solid. History Experimentally Pierre Louis Dulong and Alexis Thérèse Petit had found in 1819 that the heat capacity per weight (the mass-specific heat capacity) for 13 measured elements was close to a constant value, after it had been multiplied by a number representing the presumed relative atomic weight of the element. These atomic weights had shortly before been suggested by John Dalton and modified by Jacob Berzelius. Du ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ultraviolet Catastrophe
The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was the prediction of late 19th century and early 20th century classical physics that an ideal black body at thermal equilibrium would emit an unbounded quantity of energy as wavelength decreased into the ultraviolet range. The term "ultraviolet catastrophe" was first used in 1911 by the Austrian physicist Paul Ehrenfest, but the concept originated with the 1900 statistical derivation of the Rayleigh–Jeans law. The phrase refers to the fact that the empirically derived Rayleigh–Jeans law, which accurately predicted experimental results at large wavelengths, failed to do so for short wavelengths. (See the image for further elaboration.) As the theory diverged from empirical observations when these frequencies reached the ultraviolet region of the electromagnetic spectrum, there was a problem. This problem was later found to be due to a property of quanta as proposed by Max Planck: There could be n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black-body Radiation
Black-body radiation is the thermal radiation, thermal electromagnetic radiation within, or surrounding, a body in thermodynamic equilibrium with its environment, emitted by a black body (an idealized opaque, non-reflective body). It has a specific continuous spectrum that depends only on the body's temperature., Chapter 13. A perfectly-insulated enclosure which is in thermal equilibrium internally contains blackbody radiation and will emit it through a hole made in its wall, provided the hole is small enough to have a negligible effect upon the equilibrium. The thermal radiation spontaneously emitted by many ordinary objects can be approximated as blackbody radiation. Of particular importance, although planets and stars (including the Earth and Sun) are neither in thermal equilibrium with their surroundings nor perfect black bodies, blackbody radiation is still a good first approximation for the energy they emit. The term ''black body'' was introduced by Gustav Kirchhoff in 1860. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K). Heat capacity is an extensive property. The corresponding intensive property is the specific heat capacity, found by dividing the heat capacity of an object by its mass. Dividing the heat capacity by the amount of substance in moles yields its molar heat capacity. The volumetric heat capacity measures the heat capacity per volume. In architecture and civil engineering, the heat capacity of a building is often referred to as its '' thermal mass''. Definition Basic definition The heat capacity of an object, denoted by C, is the limit C = \lim_\frac, where \Delta Q is the amount of heat that must be added to the object (of mass ''M'') in order to raise its temperature by \Delta T. The value of this parameter usually varies considerably depending o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |