|
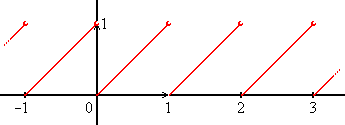
Equidistributed Mod 1
In mathematics, a sequence (''s''1, ''s''2, ''s''3, ...) of real numbers is said to be equidistributed, or uniformly distributed, if the proportion of terms falling in a subinterval is proportional to the length of that subinterval. Such sequences are studied in Diophantine approximation theory and have applications to Monte Carlo integration. Definition A sequence (''s''1, ''s''2, ''s''3, ...) of real numbers is said to be ''equidistributed'' on a non-degenerate interval 'a'', ''b''if for every subinterval 'c'', ''d''of 'a'', ''b''we have :\lim_= . (Here, the notation , ∩ 'c'', ''d'' denotes the number of elements, out of the first ''n'' elements of the sequence, that are between ''c'' and ''d''.) For example, if a sequence is equidistributed in , 2 since the interval .5, 0.9occupies 1/5 of the length of the interval , 2 as ''n'' becomes large, the proportion of the first ''n'' members of the sequence which fall between 0.5 and 0.9 must approach 1/5. L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Superior And Limit Inferior
In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting (that is, eventual and extreme) bounds on the sequence. They can be thought of in a similar fashion for a function (see limit of a function). For a set, they are the infimum and supremum of the set's limit points, respectively. In general, when there are multiple objects around which a sequence, function, or set accumulates, the inferior and superior limits extract the smallest and largest of them; the type of object and the measure of size is context-dependent, but the notion of extreme limits is invariant. Limit inferior is also called infimum limit, limit infimum, liminf, inferior limit, lower limit, or inner limit; limit superior is also known as supremum limit, limit supremum, limsup, superior limit, upper limit, or outer limit. The limit inferior of a sequence (x_n) is denoted by \liminf_x_n\quad\text\quad \varliminf_x_n, and the limit superior of a sequence (x_n) is denote ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Term
In mathematics, a constant term (sometimes referred to as a free term) is a term in an algebraic expression that does not contain any variables and therefore is constant. For example, in the quadratic polynomial, :x^2 + 2x + 3,\ The number 3 is a constant term. After like terms are combined, an algebraic expression will have at most one constant term. Thus, it is common to speak of the quadratic polynomial :ax^2+bx+c,\ where x is the variable, as having a constant term of c. If the constant term is 0, then it will conventionally be omitted when the quadratic is written out. Any polynomial written in standard form has a unique constant term, which can be considered a coefficient of x^0. In particular, the constant term will always be the lowest degree term of the polynomial. This also applies to multivariate polynomials. For example, the polynomial :x^2+2xy+y^2-2x+2y-4\ has a constant term of −4, which can be considered to be the coefficient of x^0y^0, where the va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problem (mathematics education), word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; and they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irrational Number
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being '' incommensurable'', meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself. Among irrational numbers are the ratio of a circle's circumference to its diameter, Euler's number ''e'', the golden ratio ''φ'', and the square root of two. In fact, all square roots of natural numbers, other than of perfect squares, are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the case of irrational numbers, the decimal expansion does not terminate, nor end ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equidistribution Theorem
In mathematics, the equidistribution theorem is the statement that the sequence :''a'', 2''a'', 3''a'', ... mod 1 is Equidistributed sequence, uniformly distributed on the circle \mathbb/\mathbb, when ''a'' is an irrational number. It is a special case of the ergodic theorem where one takes the normalized angle measure \mu=\frac. History While this theorem was proved in 1909 and 1910 separately by Hermann Weyl, Wacław Sierpiński and Piers Bohl, variants of this theorem continue to be studied to this day. In 1916, Weyl proved that the sequence ''a'', 22''a'', 32''a'', ... mod 1 is uniformly distributed on the unit interval. In 1937, Ivan Vinogradov proved that the sequence ''p''''n'' ''a'' mod 1 is uniformly distributed, where ''p''''n'' is the ''n''th prime number, prime. Vinogradov's proof was a byproduct of the odd Goldbach conjecture, that every sufficiently large odd number is the sum of three primes. George Birkhoff, in 1931, and Aleksandr Khinchin, in 1933, proved ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Van Der Corput Sequence 999
A van is a type of road vehicle used for transporting goods or people. There is some variation in the scope of the word across the different English-speaking countries. The smallest vans, microvans, are used for transporting either goods or people in tiny quantities. Mini MPVs, compact MPVs, and MPVs are all small vans usually used for transporting people in small quantities. Larger vans with passenger seats are used for institutional purposes, such as transporting students. Larger vans with only front seats are often used for business purposes, to carry goods and equipment. Specially equipped vans are used by television stations as mobile studios. Postal services and courier companies use large step vans to deliver packages. Word origin and usage Van meaning a type of vehicle arose as a contraction of the word caravan. The earliest records of a van as a vehicle in English are in the mid-19th century, meaning a covered wagon for transporting goods; the earliest reported r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Part
The fractional part or decimal part of a non‐negative real number x is the excess beyond that number's integer part. The latter is defined as the largest integer not greater than , called ''floor'' of or \lfloor x\rfloor. Then, the fractional part can be formulated as a difference: :\operatorname (x)=x - \lfloor x \rfloor,\; x > 0. The fractional part of logarithms, specifically, is also known as the mantissa; by contrast with the mantissa, the integral part of a logarithm is called its ''characteristic''. The word ''mantissa'' was introduced by Henry Briggs. For a positive number written in a conventional positional numeral system (such as binary or decimal), its fractional part hence corresponds to the digits appearing after the radix point, such as the decimal point in English. The result is a real number in the half-open interval x, -\lfloor , x, \rfloor , or by the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Almost Everywhere
In measure theory (a branch of mathematical analysis), a property holds almost everywhere if, in a technical sense, the set for which the property holds takes up nearly all possibilities. The notion of "almost everywhere" is a companion notion to the concept of measure zero, and is analogous to the notion of '' almost surely'' in probability theory. More specifically, a property holds almost everywhere if it holds for all elements in a set except a subset of measure zero, or equivalently, if the set of elements for which the property holds is conull. In cases where the measure is not complete, it is sufficient that the set be contained within a set of measure zero. When discussing sets of real numbers, the Lebesgue measure is usually assumed unless otherwise stated. The term ''almost everywhere'' is abbreviated ''a.e.''; in older literature ''p.p.'' is used, to stand for the equivalent French language phrase ''presque partout''. A set with full measure is one whose complement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countable Set
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (the number of elements of the set) is not greater than that of the natural numbers. A countable set that is not finite is said to be countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Counterexample
A counterexample is any exception to a generalization. In logic a counterexample disproves the generalization, and does so rigorously in the fields of mathematics and philosophy. For example, the fact that "student John Smith is not lazy" is a counterexample to the generalization "students are lazy", and both a counterexample to, and disproof of, the universal quantification "all students are lazy." In mathematics In mathematics, counterexamples are often used to prove the boundaries of possible theorems. By using counterexamples to show that certain conjectures are false, mathematical researchers can then avoid going down blind alleys and learn to modify conjectures to produce provable theorems. It is sometimes said that mathematical development consists primarily in finding (and proving) theorems and counterexamples. Rectangle example Suppose that a mathematician is studying geometry and shapes, and she wishes to prove certain theorems about them. She conjectures that "All re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |