|
Elliptic
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but for its perimeter (also known as circumference), integration is required to obtain an exact solution. The largest and smallest diameters of an ellipse, also known as its width and height, are typically denoted and . An ellipse has four extreme points: two '' vertices'' at the endpoints of the major axis and two ''co-vertices'' at the endpoints of the minor axis. Analytically, the equation of a standard ellipse centered at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylinder (geometry)
A cylinder () has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base. A cylinder may also be defined as an infinite curvilinear surface in various modern branches of geometry and topology. The shift in the basic meaning—solid versus surface (as in a solid ball versus sphere surface)—has created some ambiguity with terminology. The two concepts may be distinguished by referring to solid cylinders and cylindrical surfaces. In the literature the unadorned term "cylinder" could refer to either of these or to an even more specialized object, the '' right circular cylinder''. Types The definitions and results in this section are taken from the 1913 text ''Plane and Solid Geometry'' by George A. Wentworth and David Eugene Smith . A ' is a surface consisting of all the points on all the lines which are parallel to a given line and which pass through ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes considered a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2; that is, as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a Point (geometry), point (the Focus (geometry), focus) and a Line (geometry), line (the Directrix (conic section), directrix). The focus does not lie on the directrix. The parabola is the locus (mathematics), locus of points in that plane that are equidistant from the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane (geometry), plane Parallel (geometry), parallel to another plane that is tangential to the conical surface. The graph of a function, graph of a quadratic function y=ax^2+bx+ c (with a\neq 0 ) is a parabola with its axis parallel to the -axis. Conversely, every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbola
In mathematics, a hyperbola is a type of smooth function, smooth plane curve, curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected component (topology), connected components or branches, that are mirror images of each other and resemble two infinite bow (weapon), bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane (mathematics), plane and a double cone (geometry), cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Besides being a conic section, a hyperbola can arise as the locus (mathematics), locus of points whose difference of distances to two fixed focus (geometry), foci is constant, as a curve for each point of which the rays to two fix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the cente ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perimeter Of An Ellipse
Unlike most other elementary shapes, such as the circle and square, there is no closed-form expression for the perimeter of an ellipse. Throughout history, a large number of closed-form approximations and of expressions in terms of integrals or series have been given for the perimeter of an ellipse. Exact value Elliptic integral An ellipse is defined by two axes: the major axis (the longest diameter) of length 2a and the minor axis (the shortest diameter) of length 2b, where the quantities a and b are the lengths of the semi-major and semi-minor axes respectively. The exact perimeter P of an ellipse is given by the integral P=4a\int_^ \sqrt\ d\theta, where e is the eccentricity of the ellipse, defined as e=\sqrt. If we define the function E(x) = \int_^ \sqrt\ d\theta, known as the complete elliptic integral of the second kind, the perimeter can be expressed in terms of that function as simply P=4aE(e^2). The integral used to find the perimeter does not have a clos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
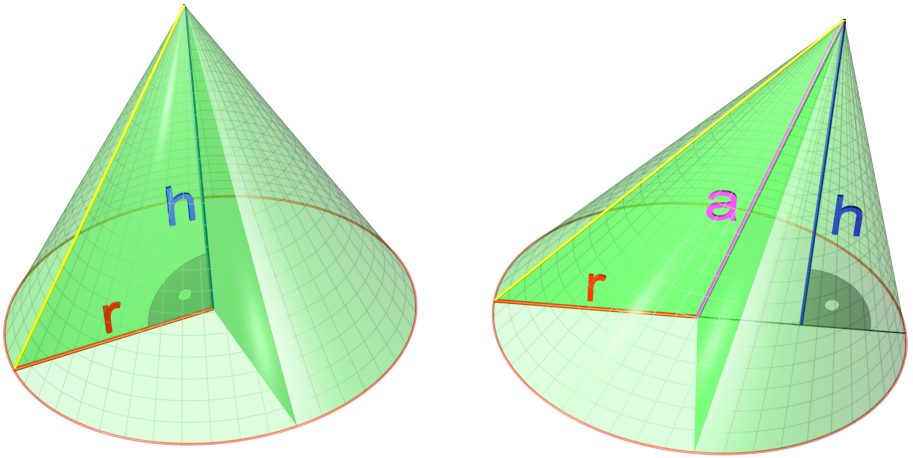
Cone
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focus (geometry)
In geometry, focuses or foci (; : focus) are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an n-ellipse, ''n''-ellipse. Conic sections Defining conics in terms of two foci An ellipse can be defined as the locus (mathematics), locus of points for which the sum of the distances to two given foci is constant. A circle is the special case of an ellipse in which the two foci coincide with each other. Thus, a circle can be more simply defined as the locus of points each of which is a fixed distance from a single given focus. A circle can also be defined as the Circles of Apollonius, circle of Apollonius, in terms of two different foci, as the locus of points having a fixed ratio of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eccentricity (mathematics)
In mathematics, the eccentricity of a Conic section#Eccentricity, conic section is a non-negative real number that uniquely characterizes its shape. One can think of the eccentricity as a measure of how much a conic section deviates from being circular. In particular: * The eccentricity of a circle is 0. * The eccentricity of a non-circular ellipse is between 0 and 1. * The eccentricity of a parabola is 1. * The eccentricity of a hyperbola is greater than 1. * The eccentricity of a pair of Line (geometry), lines is \infty. Two conic sections with the same eccentricity are similarity (geometry), similar. Definitions Any conic section can be defined as the Locus (mathematics), locus of points whose distances to a point (the focus) and a line (the directrix) are in a constant ratio. That ratio is called the ''eccentricity'', commonly denoted as . The eccentricity can also be defined in terms of the intersection of a plane and a Cone (geometry), double-napped cone associated with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Section (geometry)
In geometry and science, a cross section is the non-empty intersection (set theory), intersection of a solid body in three-dimensional space with a Plane (geometry), plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the Cartesian coordinate system, axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation. In technical drawing a cross-section, being a Planar projection, projection of an object onto a plane that intersects it, is a common tool used to depict the internal arrangement of a 3-dimensional object in two dimensions. It is traditionally crosshatched with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Eccentricity
In mathematics, the eccentricity of a conic section is a non-negative real number that uniquely characterizes its shape. One can think of the eccentricity as a measure of how much a conic section deviates from being circular. In particular: * The eccentricity of a circle is 0. * The eccentricity of a non-circular ellipse is between 0 and 1. * The eccentricity of a parabola is 1. * The eccentricity of a hyperbola is greater than 1. * The eccentricity of a pair of lines is \infty. Two conic sections with the same eccentricity are similar. Definitions Any conic section can be defined as the locus of points whose distances to a point (the focus) and a line (the directrix) are in a constant ratio. That ratio is called the ''eccentricity'', commonly denoted as . The eccentricity can also be defined in terms of the intersection of a plane and a double-napped cone associated with the conic section. If the cone is oriented with its axis vertical, the eccentricity is : e = \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumference
In geometry, the circumference () is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length around any closed figure. Circumference may also refer to the circle itself, that is, the Locus (geometry), locus corresponding to the Edge (geometry), edge of a Disk (geometry), disk. The is the circumference, or length, of any one of its great circles. Circle The circumference of a circle is the distance around it, but if, as in many elementary treatments, distance is defined in terms of straight lines, this cannot be used as a definition. Under these circumstances, the circumference of a circle may be defined as the Limit (mathematics), limit of the perimeters of inscribed regular polygons as the number of sides increases without bound. The term circumference is used when measuring physical objects, as well as when considering abstrac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |