|
Electric Susceptibility
In electricity (electromagnetism), the electric susceptibility (\chi_; Latin: ''susceptibilis'' "receptive") is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field. The greater the electric susceptibility, the greater the ability of a material to polarize in response to the field, and thereby reduce the total electric field inside the material (and store energy). It is in this way that the electric susceptibility influences the electric permittivity of the material and thus influences many other phenomena in that medium, from the capacitance of capacitors to the speed of light. Definition for linear dielectrics If a dielectric material is a linear dielectric, then electric susceptibility is defined as the constant of proportionality (which may be a tensor) relating an electric field E to the induced dielectric polarization density P such that \mathbf P =\varepsilon_0 \chi_, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interactions of atoms and molecules. Electromagnetism can be thought of as a combination of electrostatics and magnetism, which are distinct but closely intertwined phenomena. Electromagnetic forces occur between any two charged particles. Electric forces cause an attraction between particles with opposite charges and repulsion between particles with the same charge, while magnetism is an interaction that occurs between charged particles in relative motion. These two forces are described in terms of electromagnetic fields. Macroscopic charged objects are described in terms of Coulomb's law for electricity and Ampère's force law for magnetism; the Lorentz force describes microscopic charged particles. The electromagnetic force is responsible for ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clausius–Mossotti Relation
In electromagnetism, the Clausius–Mossotti relation, named for O. F. Mossotti and Rudolf Clausius, expresses the dielectric constant (relative permittivity, ) of a material in terms of the atomic polarizability, , of the material's constituent atoms and/or molecules, or a homogeneous mixture thereof. It is equivalent to the Lorentz–Lorenz equation, which relates the refractive index (rather than the dielectric constant) of a substance to its polarizability. It may be expressed as: \frac = \frac where *\varepsilon_r = \tfrac is the dielectric constant of the material, which for non-magnetic materials is equal to , where is the refractive index; * is the permittivity of free space; * is the number density of the molecules (number per cubic meter); * is the molecular polarizability in SI-units ·m2/V In the case that the material consists of a mixture of two or more species, the right hand side of the above equation would consist of the sum of the molecular polarizability c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Causality
Causality is an influence by which one Event (philosophy), event, process, state, or Object (philosophy), object (''a'' ''cause'') contributes to the production of another event, process, state, or object (an ''effect'') where the cause is at least partly responsible for the effect, and the effect is at least partly dependent on the cause. The cause of something may also be described as the reason for the event or process. In general, a process can have multiple causes,Compare: which are also said to be ''causal factors'' for it, and all lie in its past. An effect can in turn be a cause of, or causal factor for, many other effects, which all lie in its future. Some writers have held that causality is metaphysics , metaphysically prior to notions of time and space. Causality is an abstraction that indicates how the world progresses. As such it is a basic concept; it is more apt to be an explanation of other concepts of progression than something to be explained by other more fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
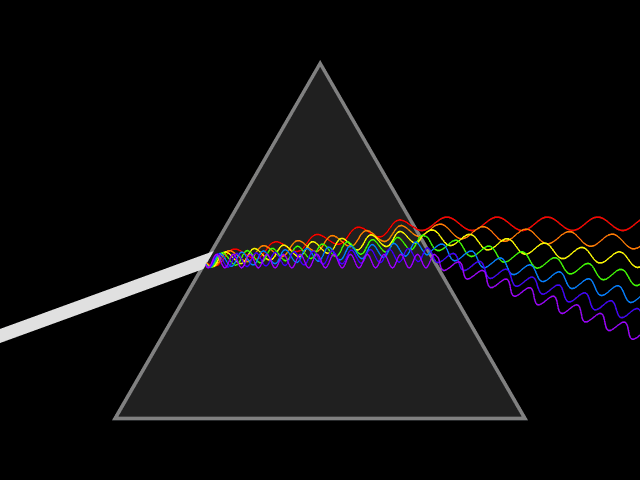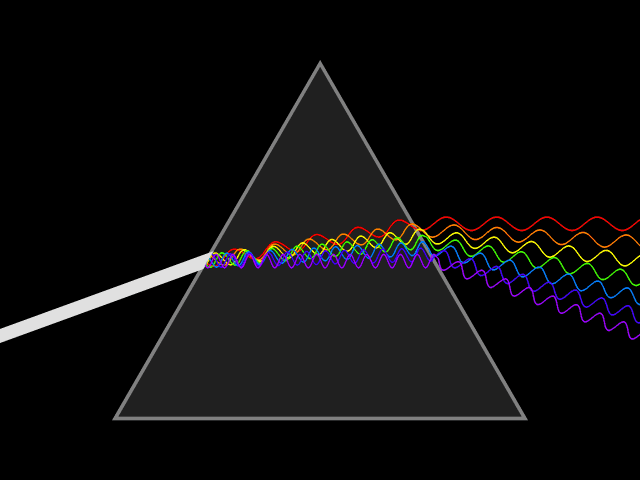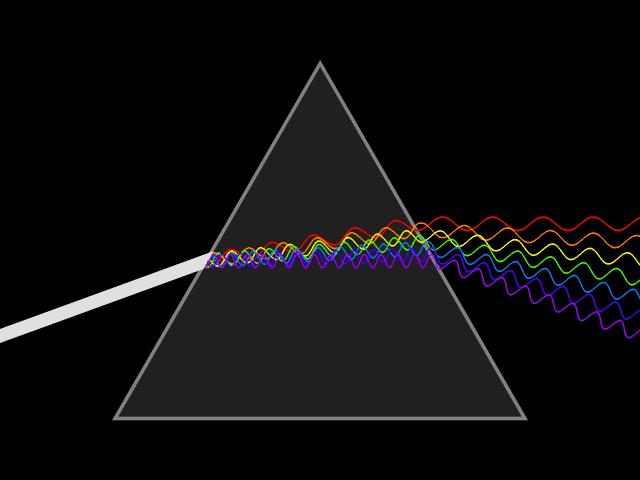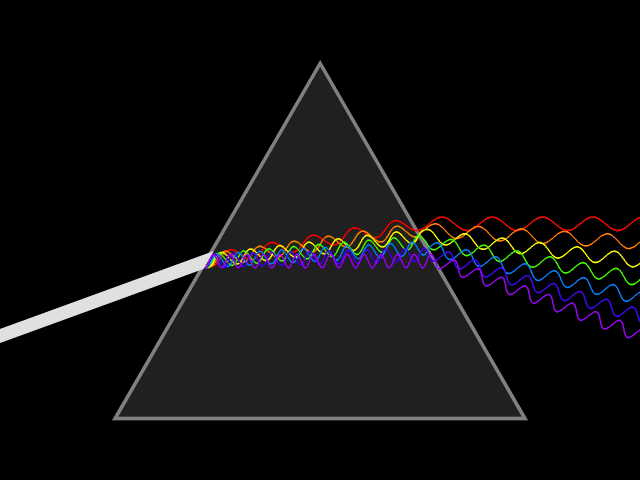
Dispersion (optics)
Dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency. Sometimes the term chromatic dispersion is used to refer to optics specifically, as opposed to wave propagation in general. A medium having this common property may be termed a dispersive medium. Although the term is used in the field of optics to describe light and other electromagnetic waves, dispersion in the same sense can apply to any sort of wave motion such as acoustic dispersion in the case of sound and seismic waves, and in gravity waves (ocean waves). Within optics, dispersion is a property of telecommunication signals along transmission lines (such as microwaves in coaxial cable) or the Pulse (signal processing), pulses of light in optical fiber. In optics, one important and familiar consequence of dispersion is the change in the angle of refraction of different colors of light, as seen in the spectrum produced by a dispersive Prism (optics), prism and in chromatic aberration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution Theorem
In mathematics, the convolution theorem states that under suitable conditions the Fourier transform of a convolution of two functions (or signals) is the product of their Fourier transforms. More generally, convolution in one domain (e.g., time domain) equals point-wise multiplication in the other domain (e.g., frequency domain). Other versions of the convolution theorem are applicable to various Fourier-related transforms. Functions of a continuous variable Consider two functions u(x) and v(x) with Fourier transforms U and V: :\begin U(f) &\triangleq \mathcal\(f) = \int_^u(x) e^ \, dx, \quad f \in \mathbb\\ V(f) &\triangleq \mathcal\(f) = \int_^v(x) e^ \, dx, \quad f \in \mathbb \end where \mathcal denotes the Fourier transform operator. The transform may be normalized in other ways, in which case constant scaling factors (typically 2\pi or \sqrt) will appear in the convolution theorem below. The convolution of u and v is defined by: :r(x) = \(x) \triangleq \int_^ u(\tau) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function (mathematics), function as input then outputs another function that describes the extent to which various Frequency, frequencies are present in the original function. The output of the transform is a complex number, complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the Operation (mathematics), mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical Chord (music), chord into the sound intensity, intensities of its constituent Pitch (music), pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the #Uncertainty principle, uncerta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be Heuristic, represented heuristically as \delta (x) = \begin 0, & x \neq 0 \\ , & x = 0 \end such that \int_^ \delta(x) dx=1. Since there is no function having this property, modelling the delta "function" rigorously involves the use of limit (mathematics), limits or, as is common in mathematics, measure theory and the theory of distribution (mathematics), distributions. The delta function was introduced by physicist Paul Dirac, and has since been applied routinely in physics and engineering to model point masses and instantaneous impulses. It is called the delta function because it is a continuous analogue of the Kronecker delta function, which is usually defined on a discrete domain and takes values ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dielectric Constant As A Function Of Light Frequency
In electromagnetism, a dielectric (or dielectric medium) is an electrical insulator that can be polarised by an applied electric field. When a dielectric material is placed in an electric field, electric charges do not flow through the material as they do in an electrical conductor, because they have no loosely bound, or free, electrons that may drift through the material, but instead they shift, only slightly, from their average equilibrium positions, causing dielectric polarisation. Because of dielectric polarisation, positive charges are displaced in the direction of the field and negative charges shift in the direction opposite to the field. This creates an internal electric field that reduces the overall field within the dielectric itself. If a dielectric is composed of weakly bonded molecules, those molecules not only become polarised, but also reorient so that their symmetry axes align to the field. The study of dielectric properties concerns storage and dissipation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ferroelectric
In physics and materials science, ferroelectricity is a characteristic of certain materials that have a spontaneous electric polarization that can be reversed by the application of an external electric field. All ferroelectrics are also piezoelectric and pyroelectric, with the additional property that their natural electrical polarization is reversible. The term is used in analogy to ferromagnetism, in which a material exhibits a permanent magnetic moment. Ferromagnetism was already known when ferroelectricity was discovered in 1920 in Rochelle salt by American physicist Joseph Valasek.See and Thus, the prefix ''ferro'', meaning iron, was used to describe the property despite the fact that most ferroelectric materials do not contain iron. Materials that are both ferroelectric ''and'' ferromagnetic are known as multiferroics. Polarization When most materials are electrically polarized, the polarization induced, ''P'', is almost exactly proportional to the applied extern ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Expansion
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laser Pointer
A laser pointer or laser pen is a (typically battery-powered) handheld device that uses a laser diode to emit a narrow low-power visible laser beam (i.e. Coherence (physics), coherent light) to highlight something of interest with a small bright colored spot. The small width of the beam and the low power of typical laser pointers make the beam itself invisible in a clean atmosphere, only showing a point of light when striking an opaque surface. Laser pointers can project a visible beam via scattering from dust particles or water droplets along the beam path. Higher-power and higher-frequency green or blue lasers may produce a beam visible even in clean air because of Rayleigh scattering from air molecules, especially when viewed in moderately-to-dimly lit conditions. The intensity of such scattering increases when these beams are viewed from angles near the beam axis. Such pointers, particularly in the green-light output range, are used as astronomical object pointers for teachi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |