|
Digital Filters
In signal processing, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is typically an electronic circuit operating on continuous-time analog signals. A digital filter system usually consists of an analog-to-digital converter (ADC) to sample the input signal, followed by a microprocessor and some peripheral components such as memory to store data and filter coefficients etc. Program Instructions (software) running on the microprocessor implement the digital filter by performing the necessary mathematical operations on the numbers received from the ADC. In some high performance applications, an FPGA or ASIC is used instead of a general purpose microprocessor, or a specialized digital signal processor (DSP) with specific paralleled architecture for expediting operations such as filter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
FIR Filter General
Firs are evergreen coniferous trees belonging to the genus ''Abies'' () in the family Pinaceae. There are approximately 48–65 extant species, found on mountains throughout much of North and Central America, Eurasia, and North Africa. The genus is most closely related to ''Keteleeria'', a small genus confined to eastern Asia. The genus name is derived from the Latin "to rise" in reference to the height of its species. The common English name originates with the Old Norse ''fyri'' or the Old Danish ''fyr''. They are large trees, reaching heights of tall with trunk diameters of when mature. Firs can be distinguished from other members of the pine family by the way in which their needle-like leaves are attached singly to the branches with a base resembling a suction cup, and by their Conifer cone, cones, which, like those of Cedrus, cedars, stand upright on the branches like candles and disintegrate at maturity. Identification of the different species is based on the size ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Cellphone
A mobile phone or cell phone is a portable telephone that allows users to make and receive calls over a radio frequency link while moving within a designated telephone service area, unlike fixed-location phones ( landline phones). This radio frequency link connects to the switching systems of a mobile phone operator, providing access to the public switched telephone network (PSTN). Modern mobile telephony relies on a cellular network architecture, which is why mobile phones are often referred to as 'cell phones' in North America. Beyond traditional voice communication, digital mobile phones have evolved to support a wide range of additional services. These include text messaging, multimedia messaging, email, and internet access (via LTE, 5G NR or Wi-Fi), as well as short-range wireless technologies like Bluetooth, infrared, and ultra-wideband (UWB). Mobile phones also support a variety of multimedia capabilities, such as digital photography, video recording, and gami ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Frequency-domain
In mathematics, physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency (and possibly phase), rather than time, as in time series. While a time-domain graph shows how a signal changes over time, a frequency-domain graph shows how the signal is distributed within different frequency bands over a range of frequencies. A complex valued frequency-domain representation consists of both the magnitude and the phase of a set of sinusoids (or other basis waveforms) at the frequency components of the signal. Although it is common to refer to the magnitude portion (the real valued frequency-domain) as the frequency response of a signal, the phase portion is required to uniquely define the signal. A given function or signal can be converted between the time and frequency domains with a pair of mathematical operators called transforms. An example is the Fourier transfor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Discrete-time
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled. Discrete time Discrete time views values of variables as occurring at distinct, separate "points in time", or equivalently as being unchanged throughout each non-zero region of time ("time period")—that is, time is viewed as a discrete variable. Thus a non-time variable jumps from one value to another as time moves from one time period to the next. This view of time corresponds to a digital clock that gives a fixed reading of 10:37 for a while, and then jumps to a new fixed reading of 10:38, etc. In this framework, each variable of interest is measured once at each time period. The number of measurements between any two time periods is finite. Measurements are typically made at sequential integer values of the variable "time". A discrete signal or discrete-time signal is a time series consisting of a sequence of quantities. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Kronecker Delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise: \delta_ = \begin 0 &\text i \neq j, \\ 1 &\text i=j. \end or with use of Iverson brackets: \delta_ = =j, For example, \delta_ = 0 because 1 \ne 2, whereas \delta_ = 1 because 3 = 3. The Kronecker delta appears naturally in many areas of mathematics, physics, engineering and computer science, as a means of compactly expressing its definition above. Generalized versions of the Kronecker delta have found applications in differential geometry and modern tensor calculus, particularly in formulations of gauge theory and topological field models. In linear algebra, the n\times n identity matrix \mathbf has entries equal to the Kronecker delta: I_ = \delta_ where i and j take the values 1,2,\cdots,n, and the inner product of vectors can be written as \mathbf\cdot\mathbf = \sum_^n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Impulse Response
In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reaction of any dynamic system in response to some external change. In both cases, the impulse response describes the reaction of the system as a function of time (or possibly as a function of some other independent variable that parameterizes the dynamic behavior of the system). In all these cases, the dynamic system and its impulse response may be actual physical objects, or may be mathematical systems of equations describing such objects. Since the impulse function contains all frequencies (see the Fourier transform of the Dirac delta function, showing infinite frequency bandwidth that the Dirac delta function has), the impulse response defines the response of a linear time-invariant system for all frequencies. Mathematical considerat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Finite Impulse Response
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely (usually decaying). The impulse response (that is, the output in response to a Kronecker delta input) of an Nth-order discrete-time FIR filter lasts exactly N+1 samples (from first nonzero element through last nonzero element) before it then settles to zero. FIR filters can be discrete-time or continuous-time, and digital or analog. Definition For a causal discrete-time FIR filter of order ''N'', each value of the output sequence is a weighted sum of the most recent input values: :\begin y &= b_0 x + b_1 x -1+ \cdots + b_N x -N\\ &= \sum_^N b_i\cdot x -i \end where: * x /math> is the input signal, * y /math> is the outpu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
1 (number)
1 (one, unit, unity) is a number, numeral, and glyph. It is the first and smallest positive integer of the infinite sequence of natural numbers. This fundamental property has led to its unique uses in other fields, ranging from science to sports, where it commonly denotes the first, leading, or top thing in a group. 1 is the unit of counting or measurement, a determiner for singular nouns, and a gender-neutral pronoun. Historically, the representation of 1 evolved from ancient Sumerian and Babylonian symbols to the modern Arabic numeral. In mathematics, 1 is the multiplicative identity, meaning that any number multiplied by 1 equals the same number. 1 is by convention not considered a prime number. In digital technology, 1 represents the "on" state in binary code, the foundation of computing. Philosophically, 1 symbolizes the ultimate reality or source of existence in various traditions. In mathematics The number 1 is the first natural number after 0. Each natural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Denominator
A fraction (from , "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. A ''common'', ''vulgar'', or ''simple'' fraction (examples: and ) consists of an integer numerator, displayed above a line (or before a slash like ), and a non-zero integer denominator, displayed below (or after) that line. If these integers are positive, then the numerator represents a number of equal parts, and the denominator indicates how many of those parts make up a unit or a whole. For example, in the fraction , the numerator 3 indicates that the fraction represents 3 equal parts, and the denominator 4 indicates that 4 parts make up a whole. The picture to the right illustrates of a cake. Fractions can be used to represent ratios and division. Thus the fraction can be used to represent the ratio 3:4 (the ratio of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
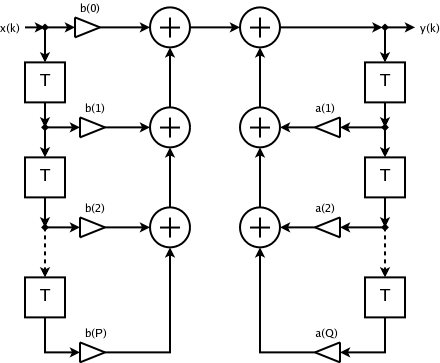 |
Infinite Impulse Response
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response h(t) that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a finite impulse response (FIR) system, in which the impulse response ''does'' become exactly zero at times t>T for some finite T, thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as ''IIR systems'' or ''IIR filters''. In practice, the impulse response, even of IIR systems, usually approaches zero and can be neglected past a certain point. However the physical systems which give rise to IIR or FIR responses are dissimilar, and therein lies the importance of the distinction. For instance, analog electronic filters composed of resistors, capacitors, and/or inductors (and perhaps linear amplifiers) are generally IIR filte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Recursive Filter
In signal processing, a recursive filter is a type of filter which reuses one or more of its outputs as an input. This feedback typically results in an unending impulse response (commonly referred to as ''infinite impulse response'' (IIR)), characterised by either exponentially growing, decaying, or sinusoidal signal output components. However, a recursive filter does not always have an infinite impulse response. Some implementations of moving average filter are recursive filters but with a finite impulse response. Non-recursive Filter Example: y = 0.5x − 1+ 0.5x Recursive Filter Example: y = 0.5y − 1+ 0.5x Examples of recursive filters *Kalman filter In statistics and control theory, Kalman filtering (also known as linear quadratic estimation) is an algorithm that uses a series of measurements observed over time, including statistical noise and other inaccuracies, to produce estimates of unk ... Signal processing {{signal-processing-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex valued frequency-domain (the z-domain or z-plane) representation. It can be considered a discrete-time equivalent of the Laplace transform (the ''s-domain'' or ''s-plane''). This similarity is explored in the theory of time-scale calculus. While the continuous-time Fourier transform is evaluated on the s-domain's vertical axis (the imaginary axis), the discrete-time Fourier transform is evaluated along the z-domain's unit circle. The s-domain's left half-plane maps to the area inside the z-domain's unit circle, while the s-domain's right half-plane maps to the area outside of the z-domain's unit circle. In signal processing, one of the means of designing digital filters is to take analog designs, subject them to a bilinear transform which maps them from the s-domain to the z-domain, and then produce the digital filter by in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |