|
Defocus
In optics, defocus is the aberration in which an image is simply out of focus. This aberration is familiar to anyone who has used a camera, videocamera, microscope, telescope, or binoculars. Optically, defocus refers to a translation of the focus along the optical axis away from the detection surface. In general, defocus reduces the sharpness and contrast of the image. What should be sharp, high-contrast edges in a scene become gradual transitions. Fine detail in the scene is blurred or even becomes invisible. Nearly all image-forming optical devices incorporate some form of focus adjustment to minimize defocus and maximize image quality. In optics and photography The degree of image blurring for a given amount of focus shift depends inversely on the lens f-number. Low f-numbers, such as to 2.8, are very sensitive to defocus and have very shallow depths of focus. High f-numbers, in the 16 to 32 range, are highly tolerant of defocus, and consequently have large depths of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bokeh Example
In photography, bokeh ( or ; ) is the aesthetic quality of the blur produced in defocus aberration, out-of-focus parts of an image, whether foreground or background or both. It is created by using a wide aperture lens. Some photographers incorrectly restrict use of the term bokeh to the appearance of bright spots in the out-of-focus area caused by Circle of confusion, circles of confusion. Bokeh has also been defined as "the way the lens renders out-of-focus points of light". Differences in optical aberration, lens aberrations and aperture shape cause very different bokeh effects. Some lens designs blur the image in a way that is pleasing to the eye, while others produce distracting or unpleasant blurring ("good" and "bad" bokeh, respectively). Photographers may deliberately use a shallow focus technique to create images with prominent out-of-focus regions, accentuating their lens's bokeh. Bokeh is often most visible around small background Point source#Light, highligh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
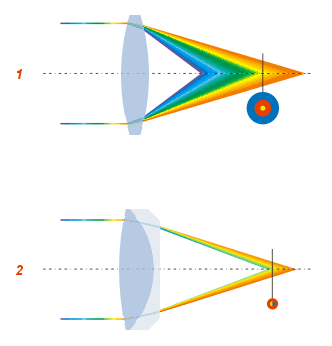
Aberration In Optical Systems
In optics, aberration is a property of optical systems, such as Lens (optics), lenses and mirrors, that causes the ''image'' created by the optical system to not be a faithful reproduction of the ''object'' being observed. Aberrations cause the image formed by a lens to be blurred, distorted in shape or have color fringing or other effects not seen in the object, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into (or does not diverge from) a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements. An image-forming optical system with aberration will produce an image which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zernike Polynomial
In mathematics, the Zernike polynomials are a sequence of polynomials that are orthogonal on the unit disk. Named after optical physicist Frits Zernike, laureate of the 1953 Nobel Prize in Physics and the inventor of phase-contrast microscopy, they play important roles in various optics branches such as beam optics and imaging. Definitions There are even and odd Zernike polynomials. The even Zernike polynomials are defined as :Z^_n(\rho,\varphi) = R^m_n(\rho)\,\cos(m\,\varphi) \! (even function over the azimuthal angle \varphi), and the odd Zernike polynomials are defined as :Z^_n(\rho,\varphi) = R^m_n(\rho)\,\sin(m\,\varphi), \! (odd function over the azimuthal angle \varphi) where ''m'' and ''n'' are nonnegative integers with ''n ≥ m ≥ 0'' (''m'' = 0 for spherical Zernike polynomials), ''\varphi'' is the azimuthal angle, ''ρ'' is the radial distance 0\le\rho\le 1, and R^m_n are the radial polynomials defined below. Zernike polynomials have the property of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focus (optics)
In geometrical optics, a focus, also called an image point, is a point where ray (optics), light rays originating from a point on the object vergence (optics), converge. Although the focus is conceptually a point, physically the focus has a spatial extent, called the circle of confusion, blur circle. This non-ideal focusing may be caused by optical aberration, aberrations of the imaging optics. Even in the absence of aberrations, the smallest possible blur circle is the Airy disc caused by diffraction from the optical system's aperture; diffraction is the ultimate limit to the light focusing ability of any optical system. Aberrations tend to worsen as the aperture diameter increases, while the Airy circle is smallest for large apertures. An image, or image point or region, is in focus if light from object points is converged almost as much as possible in the image, and defocus aberration, out of focus if light is not well converged. The border between these is sometimes define ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Resolution
Optical resolution describes the ability of an imaging system to resolve detail, in the object that is being imaged. An imaging system may have many individual components, including one or more lenses, and/or recording and display components. Each of these contributes (given suitable design, and adequate alignment) to the optical resolution of the system; the environment in which the imaging is done often is a further important factor. Lateral resolution Resolution depends on the distance between two distinguishable radiating points. The sections below describe the theoretical estimates of resolution, but the real values may differ. The results below are based on mathematical models of Airy discs, which assumes an adequate level of contrast. In low-contrast systems, the resolution may be much lower than predicted by the theory outlined below. Real optical systems are complex, and practical difficulties often increase the distance between distinguishable point sources. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Retrieval
Phase retrieval is the process of algorithmically finding solutions to the phase problem. Given a complex spectrum F(k), of amplitude , F (k), , and phase \psi(k): ::F(k) = , F(k), e^ =\int_^ f(x)\ e^\,dx where ''x'' is an ''M''-dimensional spatial coordinate and ''k'' is an ''M''-dimensional spatial frequency coordinate. Phase retrieval consists of finding the phase that satisfies a set of constraints for a measured amplitude. Important applications of phase retrieval include X-ray crystallography, transmission electron microscopy and coherent diffractive imaging, for which M = 2. Uniqueness theorems for both 1-D and 2-D cases of the phase retrieval problem, including the phaseless 1-D inverse scattering problem, were proven by Klibanov and his collaborators (see References). Problem formulation Here we consider 1-D discrete Fourier transform (DFT) phase retrieval problem. The DFT of a complex signal f[n] is given by F[k]=\sum_^ f[n] e^=, F[k], \cdot e^ \quad k=0,1, \ldots ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Microscopy
An electron microscope is a microscope that uses a beam of electrons as a source of illumination. It uses electron optics that are analogous to the glass lenses of an optical light microscope to control the electron beam, for instance focusing it to produce magnified images or electron diffraction patterns. As the wavelength of an electron can be up to 100,000 times smaller than that of visible light, electron microscopes have a much higher resolution of about 0.1 nm, which compares to about 200 nm for light microscopes. ''Electron microscope'' may refer to: * Transmission electron microscope (TEM) where swift electrons go through a thin sample * Scanning transmission electron microscope (STEM) which is similar to TEM with a scanned electron probe * Scanning electron microscope (SEM) which is similar to STEM, but with thick samples * Electron microprobe similar to a SEM, but more for chemical analysis * Low-energy electron microscope (LEEM), used to image surfaces * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Contrast
Phase-contrast imaging is a method of imaging that has a range of different applications. It measures differences in the refractive index of different materials to differentiate between structures under analysis. In conventional light microscopy, phase contrast can be employed to distinguish between structures of similar transparency, and to examine crystals on the basis of their double refraction. This has uses in biological, medical and geological science. In X-ray tomography, the same physical principles can be used to increase image contrast by highlighting small details of differing refractive index within structures that are otherwise uniform. In transmission electron microscopy (TEM), phase contrast enables very high resolution (HR) imaging, making it possible to distinguish features a few Angstrom apart (at this point highest resolution is 40 pm). Atomic physics Phase-contrast imaging is commonly used in atomic physics to describe a range of techniques for dispersively i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
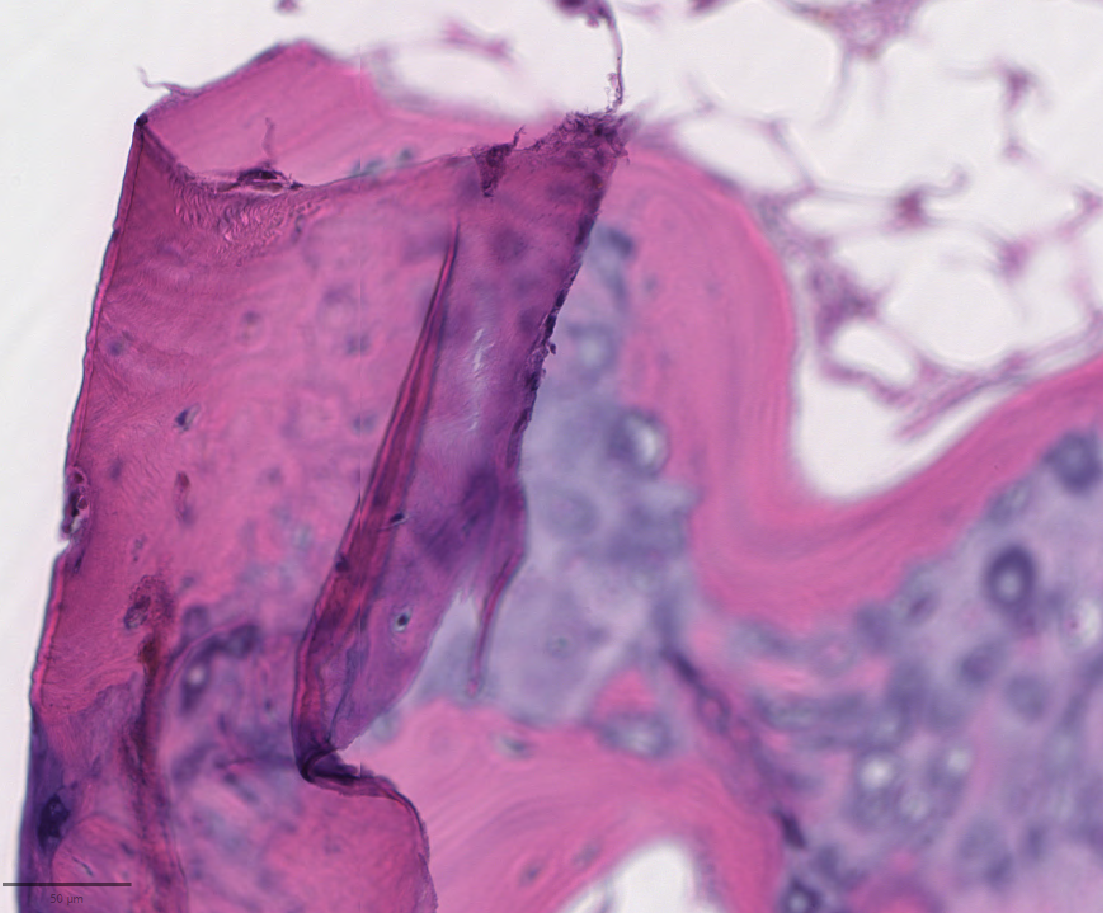
Folding Artifact On Whole Slide Imaging Of Bone
Fold, folding or foldable may refer to: Arts, entertainment, and media * ''Fold'' (album), the debut release by Australian rock band Epicure * Fold (poker), in the game of poker, to discard one's hand and forfeit interest in the current pot *Above the fold and below the fold, the positioning of news items on a newspaper's front page according to perceived importance *Paper folding, or ''origami'', the art of folding paper Science, technology, and mathematics Biology *Protein folding, the physical process by which a polypeptide folds into its characteristic and functional three-dimensional structure **Folding@home, a powerful distributed-computing project for simulating protein folding *Fold coverage, quality of a DNA sequence *Skin fold, an area of skin that folds Computing *Fold (higher-order function), a type of programming operation on data structures * fold (Unix), a computer program used to wrap lines to fit in a specified width * Folding (DSP implementation), a transformat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius Of Curvature (optics)
Radius of curvature (ROC) has specific meaning and sign convention in optical design. A spherical lens or mirror surface has a center of curvature located either along or decentered from the system local optical axis. The vertex of the lens surface is located on the local optical axis. The distance from the vertex to the center of curvature is the radius of curvature of the surface. The sign convention for the optical radius of curvature is as follows: * If the vertex lies to the left of the center of curvature, the radius of curvature is positive. * If the vertex lies to the right of the center of curvature, the radius of curvature is negative. Thus when viewing a biconvex lens from the side, the left surface radius of curvature is positive, and the right radius of curvature is negative. Note however that ''in areas of optics other than design'', other sign conventions are sometimes used. In particular, many undergraduate physics textbooks use the Gaussian sign con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Vertex
In Gaussian optics, the cardinal points consist of three pairs of Point (geometry), points located on the optical axis of a Rotational symmetry, rotationally symmetric, focal, optical system. These are the ''Focus (optics), focal points'', the principal points, and the nodal points; there are two of each. For ''ideal'' systems, the basic imaging properties such as image size, location, and orientation are completely determined by the locations of the cardinal points. For simple cases where the medium on both sides of an optical system is air or vacuum four cardinal points are sufficient: the two focal points and either the principal points or the nodal points. The only ideal system that has been achieved in practice is a plane mirror, however the cardinal points are widely used to the behavior of real optical systems. Cardinal points provide a way to analytically simplify an optical system with many components, allowing the imaging characteristics of the system to be approximatel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. The point where the tangent line and the curve meet or intersect is called the ''point of tangency''. The tangent line is said to be "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a '' tangent line approximation'', the graph of the affine function that best approximates the original function at the given point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |