|
Cuprodescloizite
Mottramite is an orthorhombic anhydrous vanadate hydroxide mineral, Pb Cu( V O4)(O H), at the copper end of the descloizite subgroup. It was formerly called cuprodescloizite or psittacinite (this mineral characterized in 1868 by Frederick Augustus Genth). Duhamelite is a calcium- and bismuth-bearing variety of mottramite, typically with acicular habit. Mottramite is a member of the adelite- descloizite group. Mottramite, which is a copper rich member, forms a series with descloizite, which is a zinc rich member. These two minerals usually contain significant percentages of both copper and zinc and are seldom pure. Mottramite also forms a series with duftite. It was discovered in 1876 and named for the locality, Mottram St Andrew, Cheshire, England, where ore was stockpiled, although it was probably mined from Pim Hill Mine, Shrewsbury, Shropshire, England.Kingsbury and Hartley (1956). New occurrences of vanadium minerals (mottramite, descloizite, (discredited) and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthorhombic
In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (''a'' by ''b'') and height (''c''), such that ''a'', ''b'', and ''c'' are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal. Bravais lattices There are four orthorhombic Bravais lattices: primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic. For the base-centered orthorhombic lattice, the primitive cell has the shape of a right rhombic prism;See , row oC, column Primitive, where the cell parameters are given as a1 = a2, α = β = 90° it can be constructed because the two-dimensional centered rectangular base layer can also be described with primitive rhombic axes. Note that the length a of the primi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal Habit
In mineralogy, crystal habit is the characteristic external shape of an individual crystal or crystal group. The habit of a crystal is dependent on its crystallographic form and growth conditions, which generally creates irregularities due to limited space in the crystallizing medium (commonly in rocks).Klein, Cornelis, 2007, ''Minerals and Rocks: Exercises in Crystal and Mineral Chemistry, Crystallography, X-ray Powder Diffraction, Mineral and Rock Identification, and Ore Mineralogy,'' Wiley, third edition, Wenk, Hans-Rudolph and Andrei Bulakh, 2004, ''Minerals: Their Constitution and Origin,'' Cambridge, first edition, Recognizing the habit can aid in mineral identification and description, as the crystal habit is an external representation of the internal ordered atomic arrangement. Most natural crystals, however, do not display ideal habits and are commonly malformed. Hence, it is also important to describe the quality of the shape of a mineral specimen: * Euhedral: a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedra
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. A convex polyhedron is the convex hull of finitely many points, not all on the same plane. Cubes and pyramids are examples of convex polyhedra. A polyhedron is a 3-dimensional example of a polytope, a more general concept in any number of dimensions. Definition Convex polyhedra are well-defined, with several equivalent standard definitions. However, the formal mathematical definition of polyhedra that are not required to be convex has been problematic. Many definitions of "polyhedron" have been given within particular contexts,. some more rigorous than others, and there is not universal agreement over which of these to choose. Some of these definitions exclude shapes that have often been counted as polyhedra (such as the self-crossing polyhedra) or include shapes that are often not considered as valid polyhe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedra
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. A regular octahedron is the dual polyhedron of a cube. It is a rectified tetrahedron. It is a square bipyramid in any of three orthogonal orientations. It is also a triangular antiprism in any of four orientations. An octahedron is the three-dimensional case of the more general concept of a cross polytope. A regular octahedron is a 3-ball in the Manhattan () metric. Regular octahedron Dimensions If the edge length of a regular octahedron is ''a'', the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is :r_u = \frac a \approx 0.707 \cdot a and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is :r_i = \frac a \approx 0.408\cdot a while the midradius, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematically, density is defined as mass divided by volume: : \rho = \frac where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate – this quantity is more specifically called specific weight. For a pure substance the density has the same numerical value as its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure. To simplify comparisons of density across different syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molar Mass
In chemistry, the molar mass of a chemical compound is defined as the mass of a sample of that compound divided by the amount of substance which is the number of moles in that sample, measured in moles. The molar mass is a bulk, not molecular, property of a substance. The molar mass is an ''average'' of many instances of the compound, which often vary in mass due to the presence of isotopes. Most commonly, the molar mass is computed from the standard atomic weights and is thus a terrestrial average and a function of the relative abundance of the isotopes of the constituent atoms on Earth. The molar mass is appropriate for converting between the mass of a substance and the amount of a substance for bulk quantities. The molecular mass and formula mass are commonly used as a synonym of molar mass, particularly for molecular compounds; however, the most authoritative sources define it differently. The difference is that molecular mass is the mass of one specific particle or m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
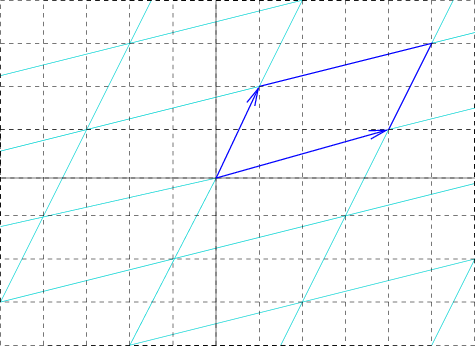
Unit Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogram or parallelepiped) that generates the whole tiling using only translations. There are two special cases of the unit cell: the primitive cell and the conventional cell. The primitive cell is a unit cell corresponding to a single lattice point, it is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Group
In mathematics, physics and chemistry, a space group is the symmetry group of an object in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of an object that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups. In crystallography, space groups are also called the crystallographic or Fedorov groups, and represent a description of the symmetry of the crystal. A definitive source regarding 3-dimensional space groups is the ''International Tables for Crystallography'' . History Space groups in 2 dimensions are the 17 wallpaper groups which have been known for several centuries, though the proof that the list was compl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal Class
In crystallography, a crystallographic point group is a set of symmetry operations, corresponding to one of the point groups in three dimensions, such that each operation (perhaps followed by a translation) would leave the structure of a crystal unchanged i.e. the same kinds of atoms would be placed in similar positions as before the transformation. For example, in many crystals in the cubic crystal system, a rotation of the unit cell by 90 degrees around an axis that is perpendicular to one of the faces of the cube is a symmetry operation that moves each atom to the location of another atom of the same kind, leaving the overall structure of the crystal unaffected. In the classification of crystals, each point group defines a so-called (geometric) crystal class. There are infinitely many three-dimensional point groups. However, the crystallographic restriction on the general point groups results in there being only 32 crystallographic point groups. These 32 point groups are one-and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthorhombic Crystal System
In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (''a'' by ''b'') and height (''c''), such that ''a'', ''b'', and ''c'' are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal. Bravais lattices There are four orthorhombic Bravais lattices: primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic. For the base-centered orthorhombic lattice, the primitive cell has the shape of a right rhombic prism;See , row oC, column Primitive, where the cell parameters are given as a1 = a2, α = β = 90° it can be constructed because the two-dimensional centered rectangular base layer can also be described with primitive rhombic axes. Note that the length a of the primit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pim Hill
Pimhill is a geographically large civil parish in Shropshire, England, to the north of Shrewsbury. It is named after a hill, which rises to 163m, sometimes spelt Pim Hill. In recent times the parish is more well known as "Bomere Heath and District". As well as the large village of Bomere Heath, the small villages of Albrighton, Atcham, Fitz, Leaton, Merrington and Preston Gubbals, as well as the hamlets of Crossgreen, Dunnsheath, Forton Heath, Grafton, Mytton, Old Woods and Walford Heath, lie in the parish. The 2001 census recorded 2008 people living in the parish, in 853 households, the population increasing to 2,118 at the 2011 Census. Near Pim Hill is Lea Hall, a notable Elizabethan brick house and dovecote. The Battle of Shrewsbury (1403) was fought in the eastern part of the parish, near the present settlement of Battlefield, though much of the battlefield now lies in the parish of Shrewsbury. The River Severn forms the parish boundary to the south, whilst the River ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mottram St Andrew
Mottram St Andrew is a village and civil parish in Cheshire, England. At the 2011 census, it had a population of 493. An affluent village in the Cheshire countryside, it is in the Golden Triangle of Alderley Edge, Prestbury and Wilmslow, 15 miles from Manchester. Mottram Hall is a hotel and golfing centre; Lower Manor is the former home of the Mottershead family. Sportsmen who have lived in the area include footballers Peter Crouch, Wayne Rooney, Owen Hargreaves, Mark Hughes, Carlos Tevez, Benjamin Mendy Benjamin Mendy (born 17 July 1994) is a French professional footballer who plays as a left-back for club Manchester City. He played for the France national team from 2017 until 2019. After coming through Le Havre's youth academy, Mendy beg ... and Mario Balotelli, cricketer Andrew Flintoff, and snooker player Alex Higgins. See also * Listed buildings in Mottram St Andrew References External links Villages in Cheshire Civil parishes in Ches ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |




.png)