|
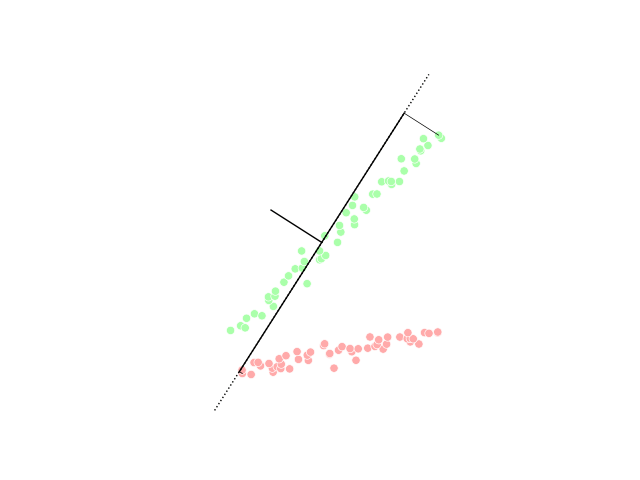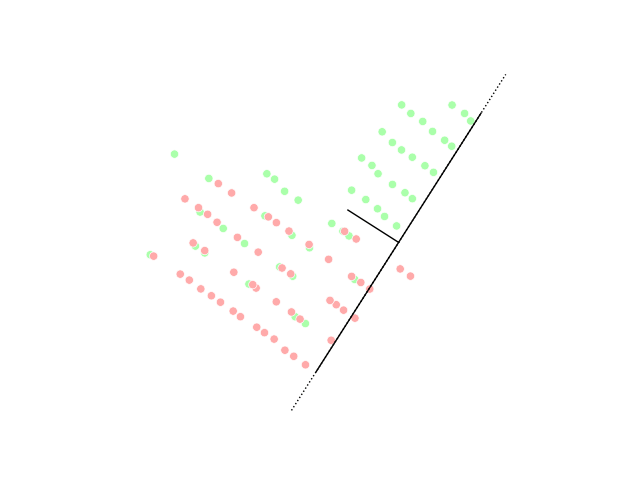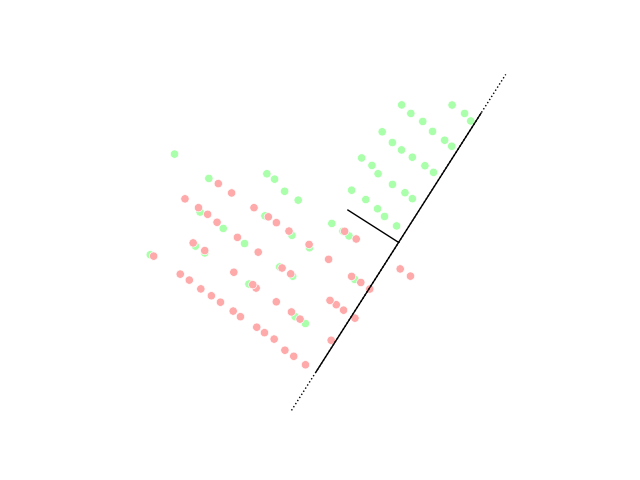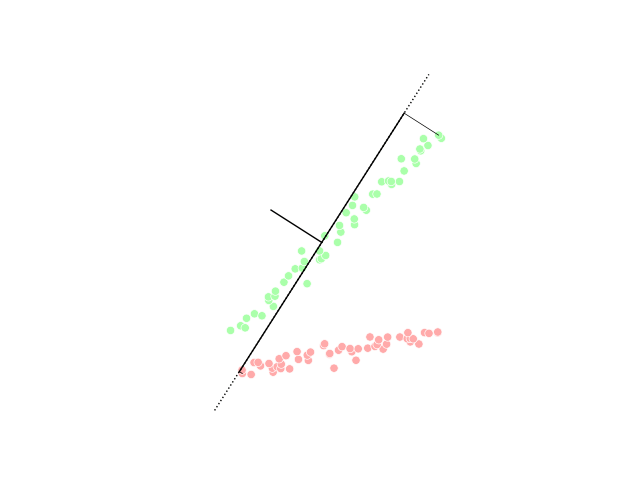
Count Sketch
Count sketch is a type of dimensionality reduction that is particularly efficient in statistics, machine learning and algorithms. It was invented by Moses Charikar, Kevin Chen and Martin Farach-Colton in an effort to speed up the AMS Sketch by Alon, Matias and Szegedy for approximating the frequency moments of streams (these calculations require counting of the number of occurrences for the distinct elements of the stream). The sketch is nearly identical to the Feature hashing algorithm by John Moody, but differs in its use of hash functions with low dependence, which makes it more practical. In order to still have a high probability of success, the median trick is used to aggregate multiple count sketches, rather than the mean. These properties allow use for explicit kernel methods, bilinear pooling in neural networks and is a cornerstone in many numerical linear algebra algorithms.Woodruff, David P. "Sketching as a Tool for Numerical Linear Algebra." Theoretical Computer S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionality Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable. Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Linear approaches can be further divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an intermediate step to facilitat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable. Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Linear approaches can be further divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an intermediate step to facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Sketch
In statistics, machine learning and algorithms, a tensor sketch is a type of dimensionality reduction that is particularly efficient when applied to Vector (mathematics and physics), vectors that have tensor structure. Such a sketch can be used to speed up explicit kernel methods, bilinear Pool (computer science), pooling in neural networks and is a cornerstone in many numerical linear algebra algorithms.Woodruff, David P.Sketching as a Tool for Numerical Linear Algebra." Theoretical Computer Science 10.1-2 (2014): 1–157. Mathematical definition Mathematically, a dimensionality reduction or sketching matrix is a matrix M\in\mathbb R^, where k |
Count–min Sketch
In computing, the count–min sketch (CM sketch) is a probabilistic data structure that serves as a frequency table of events in a stream of data. It uses hash functions to map events to frequencies, but unlike a hash table uses only sub-linear space, at the expense of overcounting some events due to collisions. The count–min sketch was invented in 2003 by Graham Cormode and S. Muthu Muthukrishnan and described by them in a 2005 paper. Count–min sketch is an alternative to count sketch and AMS sketch and can be considered an implementation of a counting Bloom filter (Fan et al., 1998) or multistage-filter. However, they are used differently and therefore sized differently: a count–min sketch typically has a sublinear number of cells, related to the desired approximation quality of the sketch, while a counting Bloom filter is more typically sized to match the number of elements in the set. Data structure The goal of the basic version of the count–min sketch is to cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Khatri–Rao Product
In mathematics, the Khatri–Rao product or block Kronecker product of two partitioned matrix, partitioned matrices \mathbf and \mathbf is defined as : \mathbf \ast \mathbf = \left(\mathbf_ \otimes \mathbf_\right)_ in which the ''ij''-th block is the sized Kronecker product of the corresponding blocks of A and B, assuming the number of row and column partitions of both Matrix (mathematics), matrices is equal. The size of the product is then . For example, if A and B both are partitioned matrices e.g.: : \mathbf = \left[ \begin \mathbf_ & \mathbf_ \\ \hline \mathbf_ & \mathbf_ \end \right] = \left[ \begin 1 & 2 & 3 \\ 4 & 5 & 6 \\ \hline 7 & 8 & 9 \end \right] ,\quad \mathbf = \left[ \begin \mathbf_ & \mathbf_ \\ \hline \mathbf_ & \mathbf_ \end \right] = \left[ \begin 1 & 4 & 7 \\ \hline 2 & 5 & 8 \\ 3 & 6 & 9 \end \right] , we obtain: : \mathbf \ast \mathbf = \left[ \begin \mathbf_ \otimes \mathbf_ & \mathbf_ \otimes \mathbf_ \\ \hline \mathbf_ \otimes \mathbf_ & \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fast Fourier Transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies. This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical. An FFT rapidly computes such transformations by Matrix decomposition, factorizing the DFT matrix into a product of Sparse matrix, sparse (mostly zero) factors. As a result, it manages to reduce the Computational complexity theory, complexity of computing the DFT from O(n^2), which arises if one simply applies the definition of DFT, to O(n \log n), where is the data size. The difference in speed can be enormous, especially for long data sets where may be in the thousands or millions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kronecker Product
In mathematics, the Kronecker product, sometimes denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It is a specialization of the tensor product (which is denoted by the same symbol) from vectors to matrices and gives the matrix of the tensor product linear map with respect to a standard choice of basis. The Kronecker product is to be distinguished from the usual matrix multiplication, which is an entirely different operation. The Kronecker product is also sometimes called matrix direct product. The Kronecker product is named after the German mathematician Leopold Kronecker (1823–1891), even though there is little evidence that he was the first to define and use it. The Kronecker product has also been called the ''Zehfuss matrix'', and the ''Zehfuss product'', after , who in 1858 described this matrix operation, but Kronecker product is currently the most widely used term. The misattribution to Kronecker rather than Zehfuss wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Outer Product
In linear algebra, the outer product of two coordinate vectors is the matrix whose entries are all products of an element in the first vector with an element in the second vector. If the two coordinate vectors have dimensions ''n'' and ''m'', then their outer product is an ''n'' × ''m'' matrix. More generally, given two tensors (multidimensional arrays of numbers), their outer product is a tensor. The outer product of tensors is also referred to as their tensor product, and can be used to define the tensor algebra. The outer product contrasts with: * The dot product (a special case of "inner product"), which takes a pair of coordinate vectors as input and produces a scalar * The Kronecker product, which takes a pair of matrices as input and produces a block matrix * Standard matrix multiplication Definition Given two vectors of size m \times 1 and n \times 1 respectively :\mathbf = \begin u_1 \\ u_2 \\ \vdots \\ u_m \end, \quad \mathbf = \begin v_1 \\ v_2 \\ \vdots \\ v_n \en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hash Collision
In computer science, a hash collision or hash clash is when two distinct pieces of data in a hash table share the same hash value. The hash value in this case is derived from a hash function which takes a data input and returns a fixed length of bits. Although hash algorithms, especially cryptographic hash algorithms, have been created with the intent of being Collision resistance, collision resistant, they can still sometimes map different data to the same hash (by virtue of the pigeonhole principle). Malicious users can take advantage of this to mimic, access, or alter data. Due to the possible negative applications of hash collisions in data management and computer security (in particular, cryptographic hash functions), collision avoidance has become an important topic in computer security. Background Hash collisions can be unavoidable depending on the number of objects in a set and whether or not the bit string they are mapped to is long enough in length. When there is a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |