|
Convex Space
In mathematics, a convex space (or barycentric algebra) is a space in which it is possible to take convex combinations of any sets of points. Formal Definition A convex space can be defined as a set X equipped with a binary convex combination operation c_\lambda : X \times X \rightarrow X for each \lambda \in ,1/math> satisfying: * c_0(x,y)=x * c_1(x,y)=y * c_\lambda(x,x)=x * c_\lambda(x,y)=c_(y,x) * c_\lambda(x,c_\mu(y,z))=c_\left(c_(x,y),z\right) (for \lambda\mu\neq 1) From this, it is possible to define an n-ary convex combination operation, parametrised by an n-tuple (\lambda_1, \dots, \lambda_n), where \sum_i\lambda_i = 1. Examples Any real affine space is a convex space. More generally, any convex subset of a real affine space is a convex space. History Convex spaces have been independently invented many times and given different names, dating back at least to Stone (1949). They were also studied by Neumann Neumann () is a German language, German surname, with its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Convex Combination
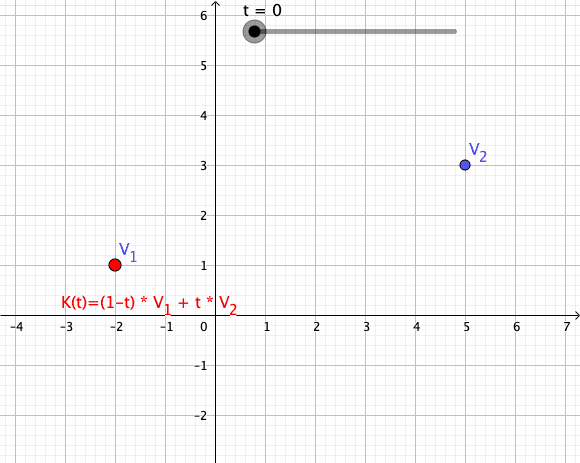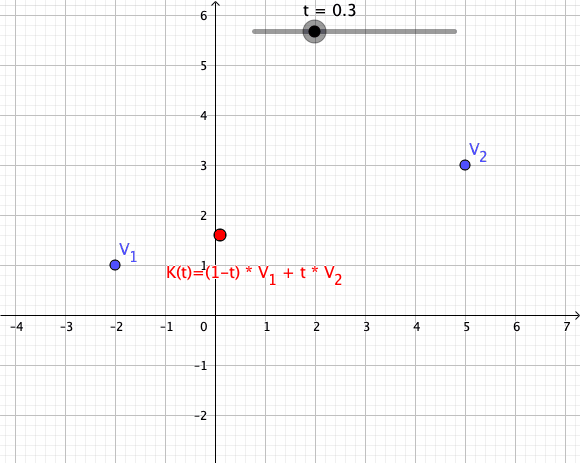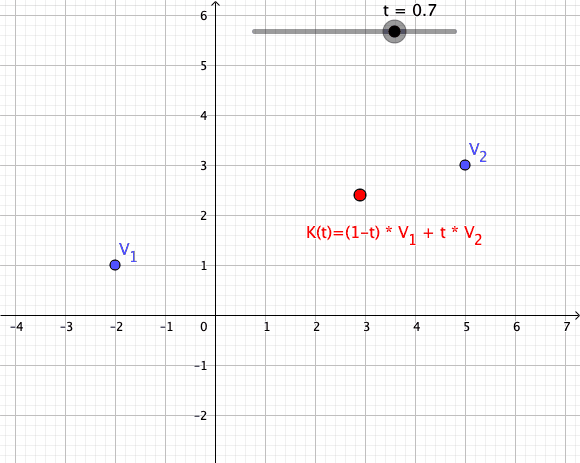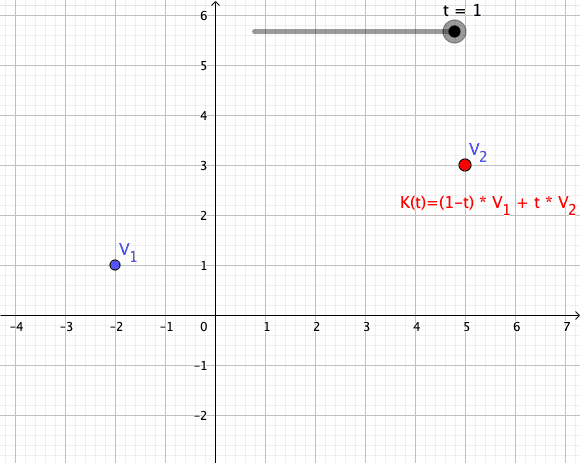
In convex geometry and Vector space, vector algebra, a convex combination is a linear combination of point (geometry), points (which can be vector (geometric), vectors, scalar (mathematics), scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. Formal definition More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form : \alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex set, convex if it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Affine Space
In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments. Affine space is the setting for affine geometry. As in Euclidean space, the fundamental objects in an affine space are called '' points'', which can be thought of as locations in the space without any size or shape: zero-dimensional. Through any pair of points an infinite straight line can be drawn, a one-dimensional set of points; through any three points that are not collinear, a two-dimensional plane can be drawn; and, in general, through points in general position, a -dimensional flat or affine subspace can be drawn. Affine space is characterized by a notion of pairs of parallel lines that lie within the same plane but never meet each-other (non-parallel lines wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Convex Subset
In geometry, a set of points is convex if it contains every line segment between two points in the set. For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary (topology), boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval (mathematics), interval with the property that its epigraph (mathematics), epigraph (the set of points on or above the graph of a function, graph of the function) is a convex set. Convex minimization is a subfield of mathematical optimization, optimization that studies the problem of minimizing convex functions over convex sets. The branch of mathematics devoted to the study of properties of convex sets and convex f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Marshall H
Marshall may refer to: Places Australia *Marshall, Victoria, a suburb of Geelong, Victoria ** Marshall railway station Canada * Marshall, Saskatchewan * The Marshall, a mountain in British Columbia Liberia * Marshall, Liberia Marshall Islands * Marshall Islands, an island nation in the Pacific Ocean United States of America * Marshall, Alaska * Marshall, Arkansas * Marshall, California * Lotus, California, former name Marshall * Marshall, Colorado * Marshall Pass, a mountain pass in Colorado * Marshall, Illinois * Marshall, Indiana * Marshall, Michigan * Marshall, Minnesota * Marshall, Missouri * Marshall, New York * Marshall, North Carolina * Marshall, North Dakota * Marshall, Oklahoma * Marshall, Texas, the largest U.S. city named Marshall * Marshall, Virginia * Marshall, Wisconsin (other) ** Marshall, Dane County, Wisconsin ** Marshall, Richland County, Wisconsin ** Marshall, Rusk County, Wisconsin Businesses * Marshall Aerospace and Defence Group, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Walter Neumann
Walter David Neumann (1 January 1946 – 24 September 2024) was a British-American mathematician who worked in topology, geometric group theory, and singularity theory. He was a professor at Barnard College, Columbia University. Neumann obtained his Ph.D. under the joint supervision of Friedrich Hirzebruch and Klaus Jänich at the University of Bonn in 1969. He was a son of the mathematicians Bernhard Neumann and Hanna Neumann. His brother Peter M. Neumann was also a mathematician. Walter Neumann was elected a member of the European Academy of Sciences in 2002. He was in the Inaugural Class of Fellows of the American Mathematical Society, starting from 2013. Neumann died on 24 September 2024, at the age of 78. Department of Mathematics, |
|
|
Convex Geometry
In mathematics, convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space. Convex sets occur naturally in many areas: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming, probability theory, game theory, etc. Classification According to the Mathematics Subject Classification MSC2010, the mathematical discipline ''Convex and Discrete Geometry'' includes three major branches: * general convexity * polytopes and polyhedra * discrete geometry (though only portions of the latter two are included in convex geometry). General convexity is further subdivided as follows: *axiomatic and generalized convexity *convex sets without dimension restrictions *convex sets in topological vector spaces *convex sets in 2 dimensions (including convex curves) *convex sets in 3 dimensions (including convex surfaces) *convex sets in ''n'' dimensions (including convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |