|
Cohomotopy Set
In mathematics, particularly algebraic topology, cohomotopy sets are particular contravariant functors from the category of pointed topological spaces and basepoint-preserving continuous maps to the category of sets and functions. They are dual to the homotopy groups, but less studied. Overview The ''p''-th cohomotopy set of a pointed topological space ''X'' is defined by :\pi^p(X) = ,S^p/math> the set of pointed homotopy classes of continuous mappings from X to the ''p''-sphere S^p. For ''p'' = 1 this set has an abelian group structure, and is called the Bruschlinsky group. Provided X is a CW-complex, it is isomorphic to the first cohomology group H^1(X), since the circle S^1 is an Eilenberg–MacLane space of type K(\mathbb,1). A theorem of Heinz Hopf states that if X is a CW-complex of dimension at most ''p'', then ,S^p/math> is in bijection with the ''p''-th cohomology group H^p(X). The set ,S^p/math> also has a natural group structure if X is a suspension \Sigm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Isomorphism
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure (i.e., the composition of morphisms) of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Informally, the notion of a natural transformation states that a particular map between functors can be done consistently over an entire category. Indeed, this intuition can be formalized to define so-called functor categories. Natural transformations are, after categories and functors, one of the most fundamental notions of category theory and consequently appear in the majority of its applications. Definition If F and G are functors between the categories C and D (both from C to D), then a natural transformation \eta from F to G is a family of morphisms that satisfies two requirements. # The natural transformation must associate, to every object X in C, a mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a Neighbourhood (mathematics), neighborhood that is homeomorphic to an open (topology), open subset of n-dimensional Euclidean space. One-dimensional manifolds include Line (geometry), lines and circles, but not Lemniscate, self-crossing curves such as a figure 8. Two-dimensional manifolds are also called Surface (topology), surfaces. Examples include the Plane (geometry), plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smooth Function
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives (''differentiability class)'' it has over its domain. A function of class C^k is a function of smoothness at least ; that is, a function of class C^k is a function that has a th derivative that is continuous in its domain. A function of class C^\infty or C^\infty-function (pronounced C-infinity function) is an infinitely differentiable function, that is, a function that has derivatives of all orders (this implies that all these derivatives are continuous). Generally, the term smooth function refers to a C^-function. However, it may also mean "sufficiently differentiable" for the problem under consideration. Differentiability classes Differentiability class is a classification of functions according to the properties of their derivatives. It is a measure of the highest order of derivative that exists and is continuous for a function. Consider an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smooth Manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a vector space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Space
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces. One suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact space, compact manifolds of the same dimension, set up using the concept of the boundary (topology), boundary (French ''wikt:bord#French, bord'', giving ''cobordism'') of a manifold. Two manifolds of the same dimension are ''cobordant'' if their disjoint union is the ''boundary'' of a compact manifold one dimension higher. The boundary of an (n+1)-dimensional manifold W is an n-dimensional manifold \partial W that is closed, i.e., with empty boundary. In general, a closed manifold need not be a boundary: cobordism theory is the study of the difference between all closed manifolds and those that are boundaries. The theory was originally developed by René Thom for smooth manifolds (i.e., differentiable), but there are now also versions for Piecewise linear manifold, piecewise linear and topological manifolds. A ''cobordism'' between manifolds M and N is a compact manifold W whose boundary is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lev Pontryagin
Lev Semyonovich Pontryagin (, also written Pontriagin or Pontrjagin, first name sometimes anglicized as Leon) (3 September 1908 – 3 May 1988) was a Soviet mathematician. Completely blind from the age of 14, he made major discoveries in a number of fields of mathematics, including algebraic topology, differential topology and optimal control. Early life and career He was born in Moscow and lost his eyesight completely due to an unsuccessful eye surgery after a primus stove explosion when he was 14. His mother Tatyana Andreyevna, who did not know mathematical symbols, read mathematical books and papers (notably those of Heinz Hopf, J. H. C. Whitehead, and Hassler Whitney) to him, and later worked as his secretary. His mother used alternative names for math symbols, such as "tails up" for the set-union symbol \cup. In 1925 he entered Moscow State University, where he was strongly influenced by the lectures of Pavel Alexandrov who would become his doctoral thesis advisor. After ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
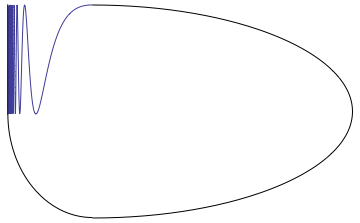
Warsaw Circle
Shape theory is a branch of topology that provides a more global view of the topological spaces than homotopy theory. The two coincide on compacta dominated homotopically by finite polyhedra. Shape theory associates with the Čech homology theory while homotopy theory associates with the singular homology theory. Background Shape theory was invented and published by D. E. Christie in 1944; it was reinvented, further developed and promoted by the Polish mathematician Karol Borsuk in 1968. Actually, the name ''shape theory'' was coined by Borsuk. Warsaw circle Borsuk lived and worked in Warsaw, hence the name of one of the fundamental examples of the area, the Warsaw circle. . Math 205B-2012 Lecture Notes, University of California Riverside. Retrieved ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Suspension (topology)
In topology, a branch of mathematics, the suspension of a topological space ''X'' is intuitively obtained by stretching ''X'' into a cylinder and then collapsing both end faces to points. One views ''X'' as "suspended" between these end points. The suspension of ''X'' is denoted by ''SX'' or susp(''X''). There is a variant of the suspension for a pointed space, which is called the reduced suspension and denoted by Σ''X''. The "usual" suspension ''SX'' is sometimes called the unreduced suspension, unbased suspension, or free suspension of ''X'', to distinguish it from Σ''X.'' Free suspension The (free) suspension SX of a topological space X can be defined in several ways. 1. SX is the quotient space (X \times ,1/(X\times \)\big/ ( X\times \). In other words, it can be constructed as follows: * Construct the cylinder X \times ,1/math>. * Consider the entire set X\times \ as a single point ("glue" all its points together). * Consider the entire set X\times \ as a single p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set with an Binary operation, operation that combines any two elements of the set to produce a third element within the same set and the following conditions must hold: the operation is Associative property, associative, it has an identity element, and every element of the set has an inverse element. For example, the integers with the addition, addition operation form a group. The concept of a group was elaborated for handling, in a unified way, many mathematical structures such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry, groups arise naturally in the study of symmetries and geometric transformations: The symmetries of an object form a group, called the symmetry group of the object, and the transformations of a given type form a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |