|
Coefficient Of Thermal Expansion
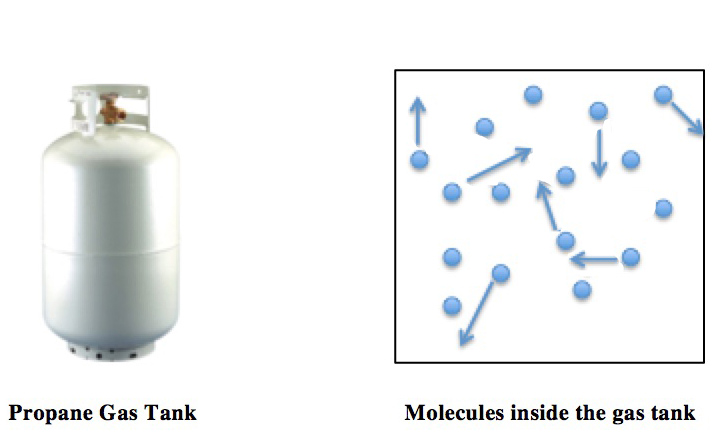
Thermal expansion is the tendency of matter to increase in length, area, or volume, changing its size and density, in response to an increase in temperature (usually excluding phase transitions). Substances usually contract with decreasing temperature (thermal contraction), with rare exceptions within limited temperature ranges ('' negative thermal expansion''). Temperature is a monotonic function of the average molecular kinetic energy of a substance. As energy in particles increases, they start moving faster and faster, weakening the intermolecular forces between them and therefore expanding the substance. When a substance is heated, molecules begin to vibrate and move more, usually creating more distance between themselves. The relative expansion (also called strain) divided by the change in temperature is called the material's coefficient of linear thermal expansion and generally varies with temperature. Prediction If an equation of state is available, it can be used t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glass
Glass is an amorphous (non-crystalline solid, non-crystalline) solid. Because it is often transparency and translucency, transparent and chemically inert, glass has found widespread practical, technological, and decorative use in window panes, tableware, and optics. Some common objects made of glass are named after the material, e.g., a Tumbler (glass), "glass" for drinking, "glasses" for vision correction, and a "magnifying glass". Glass is most often formed by rapid cooling (quenching) of the Melting, molten form. Some glasses such as volcanic glass are naturally occurring, and obsidian has been used to make arrowheads and knives since the Stone Age. Archaeological evidence suggests glassmaking dates back to at least 3600 BC in Mesopotamia, Ancient Egypt, Egypt, or Syria. The earliest known glass objects were beads, perhaps created accidentally during metalworking or the production of faience, which is a form of pottery using lead glazes. Due to its ease of formability int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Halide
In chemistry, a halide (rarely halogenide) is a binary chemical compound, of which one part is a halogen atom and the other part is an element or radical that is less electronegative (or more electropositive) than the halogen, to make a fluoride, chloride, bromide, iodide, astatide, or theoretically tennesside compound. The alkali metals combine directly with halogens under appropriate conditions forming halides of the general formula, MX (X = F, Cl, Br or I). Many salts are halides; the ''hal-'' syllable in ''halide'' and '' halite'' reflects this correlation. A halide ion is a halogen atom bearing a negative charge. The common halide anions are fluoride (), chloride (), bromide (), and iodide (). Such ions are present in many ionic halide salts. Halide minerals contain halides. All these halide anions are colorless. Halides also form covalent bonds, examples being colorless TiF4, colorless TiCl4, orange TiBr4, and brown TiI4. The heavier members TiCl4, TiBr4 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coefficient Dilatation Lineique Aciers
In mathematics, a coefficient is a multiplicative factor involved in some term of a polynomial, a series, or any other type of expression. It may be a number without units, in which case it is known as a numerical factor. It may also be a constant with units of measurement, in which it is known as a constant multiplier. In general, coefficients may be any expression (including variables such as , and ). When the combination of variables and constants is not necessarily involved in a product, it may be called a ''parameter''. For example, the polynomial 2x^2-x+3 has coefficients 2, −1, and 3, and the powers of the variable x in the polynomial ax^2+bx+c have coefficient parameters a, b, and c. A , also known as constant term or simply constant, is a quantity either implicitly attached to the zeroth power of a variable or not attached to other variables in an expression; for example, the constant coefficients of the expressions above are the number 3 and the parameter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and Thermodynamic temperature, temperature respectively; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory of gases, kinetic theory, as was achieved (independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state function, state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropy
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ocean Current
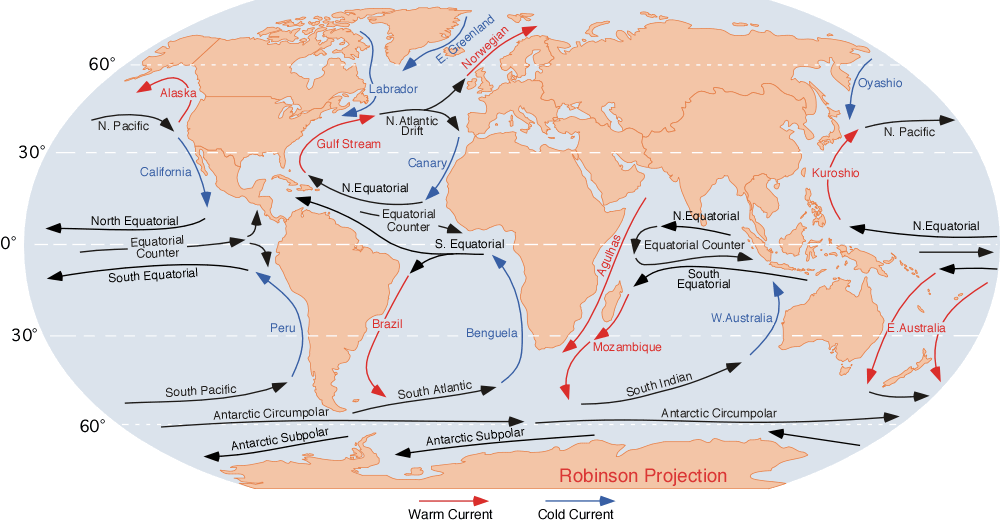
An ocean current is a continuous, directed movement of seawater generated by a number of forces acting upon the water, including wind, the Coriolis effect, breaking waves, cabbeling, and temperature and salinity differences. Depth contours, shoreline configurations, and interactions with other currents influence a current's direction and strength. Ocean currents move both horizontally, on scales that can span entire oceans, as well as vertically, with vertical currents (upwelling and downwelling) playing an important role in the movement of nutrients and gases, such as carbon dioxide, between the surface and the deep ocean. Ocean currents flow for great distances and together they create the global conveyor belt, which plays a dominant role in determining the climate of many of Earth's regions. More specifically, ocean currents influence the temperature of the regions through which they travel. For example, warm currents traveling along more temperate coasts increase the temper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wind
Wind is the natural movement of atmosphere of Earth, air or other gases relative to a planetary surface, planet's surface. Winds occur on a range of scales, from thunderstorm flows lasting tens of minutes, to local breezes generated by heating of land surfaces and lasting a few hours, to global winds resulting from the difference in absorption (electromagnetic radiation), absorption of solar energy between the climate zones on Earth. The study of wind is called anemology. The two main causes of large-scale atmospheric circulation are the differential heating between the equator and the poles, and the rotation of the planet (Coriolis effect). Within the tropics and subtropics, thermal low circulations over terrain and high plateaus can drive monsoon circulations. In coastal areas the sea breeze/land breeze cycle can define local winds; in areas that have variable terrain, mountain and valley breezes can prevail. Winds are commonly classified by their scale (spatial), spatial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convection
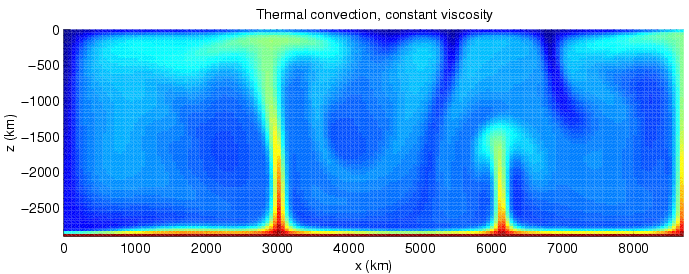
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be Transient state, transient (such as when a Multiphasic liquid, multiphase mixture of oil and water separates) or steady state (see convection cell). The convection may be due to Gravity, gravitational, Electromagnetism, electromagnetic or Fictitious force, fictitious body forces. Convection (heat transfer), Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its Earth's mantle, mantle. Discrete convective cells in the atmosphere can be identified by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Buoyant Force
Buoyancy (), or upthrust, is the force exerted by a fluid opposing the weight of a partially or fully immersed object (which may be also be a parcel of fluid). In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus, the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and (as explained by Archimedes' principle) is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the displaced fluid. For this reason, an object with average density greater than the surrounding fluid tends to sink because its weight is greater than the weight of the fluid it displaces. If the object is less dense, buoy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass–energy Equivalence
In physics, mass–energy equivalence is the relationship between mass and energy in a system's rest frame. The two differ only by a multiplicative constant and the units of measurement. The principle is described by the physicist Albert Einstein's formula: E = mc^2. In a reference frame where the system is moving, its relativistic energy and relativistic mass (instead of rest mass) obey the same formula. The formula defines the energy () of a particle in its rest frame as the product of mass () with the speed of light squared (). Because the speed of light is a large number in everyday units (approximately ), the formula implies that a small amount of mass corresponds to an enormous amount of energy. Rest mass, also called invariant mass, is a fundamental physical property of matter, independent of velocity. Massless particles such as photons have zero invariant mass, but massless free particles have both momentum and energy. The equivalence principle implies that w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |