|
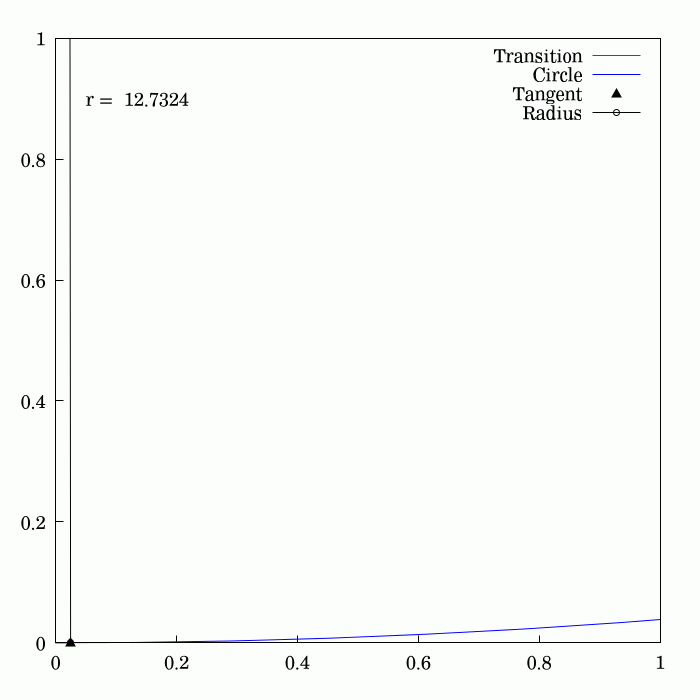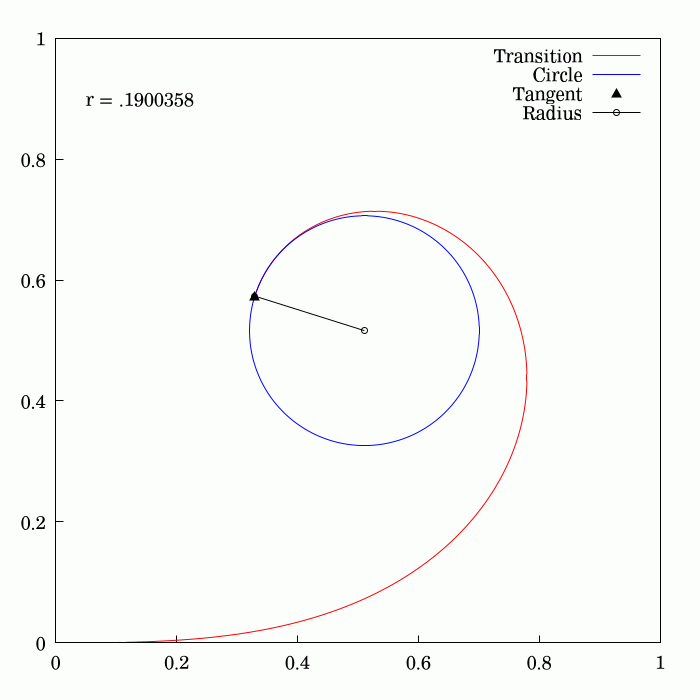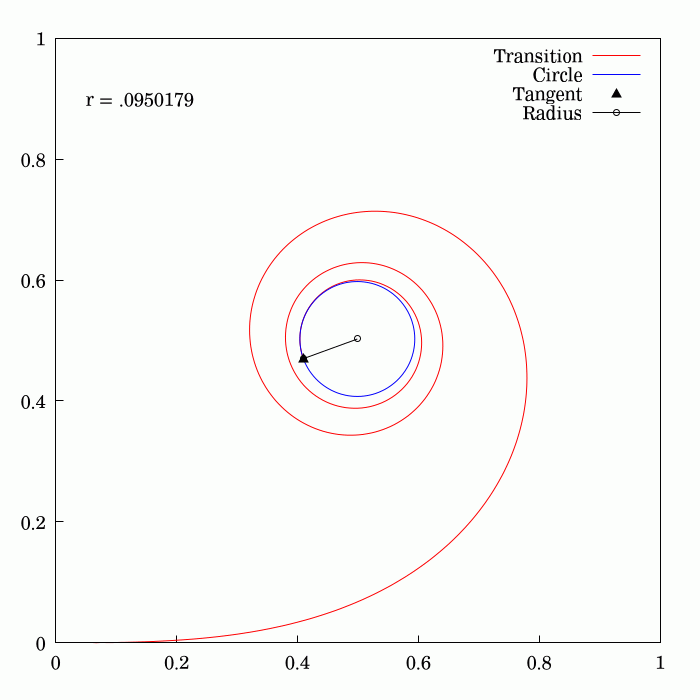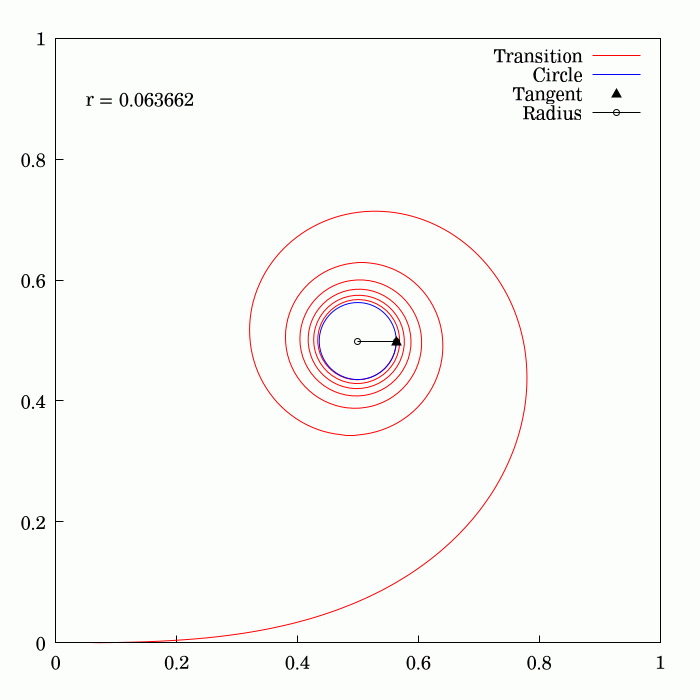
Clothoid
An Euler spiral is a curve whose curvature changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). Euler spirals are also commonly referred to as spiros, clothoids, or Cornu spirals. Euler spirals have applications to diffraction computations. They are also widely used in railway and highway engineering to design transition curves between straight and curved sections of railway or roads. A similar application is also found in photonic integrated circuits. The principle of linear variation of the curvature of the transition curve between a tangent and a circular curve defines the geometry of the Euler spiral: *Its curvature begins with zero at the straight section (the tangent) and increases linearly with its curve length. *Where the Euler spiral meets the circular curve, its curvature becomes equal to that of the latter. Applications Track transition curve To travel along a circular path, an object needs to be su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fresnel Integral
250px, Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below). The Fresnel integrals and are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function (). They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations: S(x) = \int_0^x \sin\left(t^2\right)\,dt, \quad C(x) = \int_0^x \cos\left(t^2\right)\,dt. The simultaneous parametric plot of and is the Euler spiral (also known as the Cornu spiral or clothoid). Definition 250px, Fresnel integrals with arguments instead of converge to instead of . The Fresnel integrals admit the following power series expansions that converge for all : \begin S(x) &= \int_0^x \sin\left(t^2\right)\,dt = \sum_^(-1)^n \frac, \\ C(x) &= \int_0^x \cos\left(t^2\right)\,dt = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Easement Curve
A track transition curve, or spiral easement, is a mathematically-calculated curve on a section of highway, or railroad track, in which a straight section changes into a curve. It is designed to prevent sudden changes in lateral (or centripetal) acceleration. In plane (viewed from above), the start of the transition of the horizontal curve is at infinite radius, and at the end of the transition, it has the same radius as the curve itself and so forms a very broad spiral. At the same time, in the vertical plane, the outside of the curve is gradually raised until the correct degree of bank is reached. If such an easement were not applied, the lateral acceleration of a rail vehicle would change abruptly at one point (the tangent point where the straight track meets the curve) with undesirable results. With a road vehicle, a transition curve allows the driver to alter the steering in a gradual manner. History On early railroads, because of the low speeds and wide-radius curves e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Spiral
An Euler spiral is a curve whose curvature changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). Euler spirals are also commonly referred to as spiros, clothoids, or Cornu spirals. Euler spirals have applications to diffraction computations. They are also widely used in railway and highway engineering to design transition curves between straight and curved sections of railway or roads. A similar application is also found in photonic integrated circuits. The principle of linear variation of the curvature of the transition curve between a tangent and a circular curve defines the geometry of the Euler spiral: *Its curvature begins with zero at the straight section (the tangent) and increases linearly with its curve length. *Where the Euler spiral meets the circular curve, its curvature becomes equal to that of the latter. Applications Track transition curve To travel along a circular path, an object needs to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jerk (physics)
In physics, jerk or jolt is the rate at which an object's acceleration changes with respect to time. It is a vector quantity (having both magnitude and direction). Jerk is most commonly denoted by the symbol and expressed in m/s3 (SI units) or standard gravities per second (''g''0/s). Expressions As a vector, jerk can be expressed as the first time derivative of acceleration, second time derivative of velocity, and third time derivative of position: \mathbf j(t) = \frac = \frac = \frac where * is acceleration * is velocity * is position * is time Third-order differential equations of the form J\left(\overset, \ddot, \dot, x\right) = 0 are sometimes called ''jerk equations''. When converted to an equivalent system of three ordinary first-order non-linear differential equations, jerk equations are the minimal setting for solutions showing chaotic behaviour. This condition generates mathematical interest in ''jerk systems''. Systems involving fourth-order derivatives or hi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marie Alfred Cornu
Marie Alfred Cornu (; 6 March 1841 – 12 April 1902) was a French physicist. The French generally refer to him as Alfred Cornu. Life Cornu was born at Orléans to François Cornu and Sophie Poinsellier. He was educated at the École polytechnique and the École des mines. Upon the death of Émile Verdet in 1866, Cornu became, in 1867, Verdet's successor as professor of experimental physics at the École polytechnique, where he remained throughout his life. Although he made various excursions into other branches of physical science, undertaking, for example, with Jean-Baptistin Baille about 1870 a repetition of Cavendish's experiment for determining the gravitational constant ''G'', his original work was mainly concerned with optics and spectroscopy. In particular he carried out a classical redetermination of the speed of light by A. H. L. Fizeau's method (see Fizeau-Foucault Apparatus), introducing various improvements in the apparatus, which added greatly to the accuracy of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Raph Levien
Raphael Linus Levien (also known as Raph Levien; born April 6, 1970) is a software developer, a member of the free software developer community, through his creation of the Advogato virtual community and his work with the free software branch of Ghostscript. From 2007 until 2018, and from 2021 onwards, he was employed at Google. He holds a PhD in Computer Science from UC Berkeley. He also made a computer-assisted proof system similar to MetamathGhilbert In April 2016, Levien announced a text editor made as a " 20% Project" (Google allows some employees to spend 20% of their working hours developing their own projects)Xi Imaging and typography The primary focus of Levien's work and research is in the varied areas regarding the theory of imaging—that is, rendering pictures and fonts for electronic display, which in addition to being aesthetically and mathematically important also contribute to the accessibility and search-openness of the web. Levien has written several papers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedean Spiral
The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates it can be described by the equation r = a + b\cdot\theta with real numbers and . Changing the parameter moves the centerpoint of the spiral outward from the origin (positive toward and negative toward ) essentially through a rotation of the spiral, while controls the distance between loops. From the above equation, it can thus be stated: position of particle from point of start is proportional to angle as time elapses. Archimedes described such a spiral in his book '' On Spirals''. Conon of Samos was a friend of his and Pappus states that this spiral was discovered by Conon. Derivation of general equation of spiral A ph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Series
In mathematics, a power series (in one variable) is an infinite series of the form \sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots where ''an'' represents the coefficient of the ''n''th term and ''c'' is a constant. Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functions. In fact, Borel's theorem implies that every power series is the Taylor series of some smooth function. In many situations, ''c'' (the ''center'' of the series) is equal to zero, for instance when considering a Maclaurin series. In such cases, the power series takes the simpler form \sum_^\infty a_n x^n = a_0 + a_1 x + a_2 x^2 + \dots. Beyond their role in mathematical analysis, power series also occur in combinatorics as generating functions (a kind of formal power series) and in electronic engineering (under the name of the Z-transform). The familiar decimal notation for real numbers can also be viewe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Stability
In the mathematical subfield of numerical analysis, numerical stability is a generally desirable property of numerical algorithms. The precise definition of stability depends on the context. One is numerical linear algebra and the other is algorithms for solving ordinary and partial differential equations by discrete approximation. In numerical linear algebra, the principal concern is instabilities caused by proximity to singularities of various kinds, such as very small or nearly colliding eigenvalues. On the other hand, in numerical algorithms for differential equations the concern is the growth of round-off errors and/or small fluctuations in initial data which might cause a large deviation of final answer from the exact solution. Some numerical algorithms may damp out the small fluctuations (errors) in the input data; others might magnify such errors. Calculations that can be proven not to magnify approximation errors are called ''numerically stable''. One of the common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Osculation
In differential geometry, an osculating curve is a plane curve from a given family that has the highest possible order of contact with another curve. That is, if ''F'' is a family of smooth curves, ''C'' is a smooth curve (not in general belonging to ''F''), and ''p'' is a point on ''C'', then an osculating curve from ''F'' at ''p'' is a curve from ''F'' that passes through ''p'' and has as many of its derivatives at ''p'' equal to the derivatives of ''C'' as possible... The term derives from the Latinate root "osculate", to kiss, because the two curves contact one another in a more intimate way than simple tangency. Examples Examples of osculating curves of different orders include: *The tangent line to a curve ''C'' at a point ''p'', the osculating curve from the family of straight lines. The tangent line shares its first derivative (slope) with ''C'' and therefore has first-order contact with ''C''.. *The osculating circle to ''C'' at ''p'', the osculating curve from the fami ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Whiskers
Vibrissae (; singular: vibrissa; ), more generally called Whiskers, are a type of stiff, functional hair used by mammals to sense their environment. These hairs are finely specialised for this purpose, whereas other types of hair are coarser as tactile sensors. Although whiskers are specifically those found around the face, vibrissae are known to grow in clusters at various places around the body. Most mammals have them, including all non-human primates and especially nocturnal mammals. Whiskers are sensitive tactile hairs that aid navigation, locomotion, exploration, hunting, social touch and perform other functions. This article is primarily about the specialised sensing hairs of mammals, but some birds, fish, insects, crustaceans and other arthropods are known to have similar structures also used to sense the environment. Etymology Vibrissae (from Latin 'to vibrate') from the characteristic motion seen in a small rodent that is otherwise sitting still. In medicine, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
YouTube
YouTube is a global online video sharing and social media platform headquartered in San Bruno, California. It was launched on February 14, 2005, by Steve Chen, Chad Hurley, and Jawed Karim. It is owned by Google, and is the second most visited website, after Google Search. YouTube has more than 2.5 billion monthly users who collectively watch more than one billion hours of videos each day. , videos were being uploaded at a rate of more than 500 hours of content per minute. In October 2006, YouTube was bought by Google for $1.65 billion. Google's ownership of YouTube expanded the site's business model, expanding from generating revenue from advertisements alone, to offering paid content such as movies and exclusive content produced by YouTube. It also offers YouTube Premium, a paid subscription option for watching content without ads. YouTube also approved creators to participate in Google's AdSense program, which seeks to generate more revenue for both parties. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpeg/1200px-Brusio_Viaduct_(158241421).jpeg)



