|
Cellular Automaton
A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling. A cellular automaton consists of a regular grid of ''cells'', each in one of a finite number of ''State (computer science), states'', such as ''on'' and ''off'' (in contrast to a coupled map lattice). The grid can be in any finite number of dimensions. For each cell, a set of cells called its ''neighborhood'' is defined relative to the specified cell. An initial state (time ''t'' = 0) is selected by assigning a state for each cell. A new ''generation'' is created (advancing ''t'' by 1), according to some fixed ''rule'' (generally, a mathematical function) that dete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Cellular Automaton
In mathematics and computability theory, an elementary cellular automaton is a one-dimensional cellular automaton where there are two possible states (labeled 0 and 1) and the rule to determine the state of a cell in the next generation depends only on the current state of the cell and its two immediate neighbors. There is an elementary cellular automaton (rule 110, defined below) which is capable of universal computation, and as such it is one of the simplest possible models of computation. The numbering system There are 8 = 23 possible configurations for a cell and its two immediate neighbors. The rule defining the cellular automaton must specify the resulting state for each of these possibilities so there are 256 = 223 possible elementary cellular automata. Stephen Wolfram proposed a scheme, known as the Wolfram code, to assign each rule a number from 0 to 255 which has become standard. Each possible current configuration is written in order, 111, 110, ..., 001, 000, and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
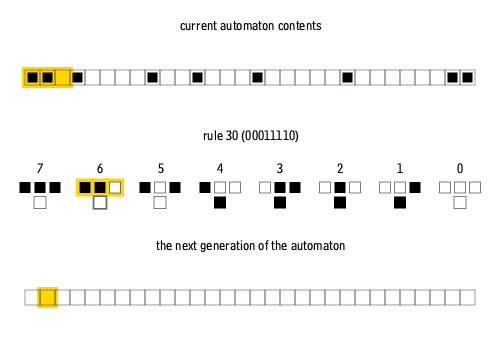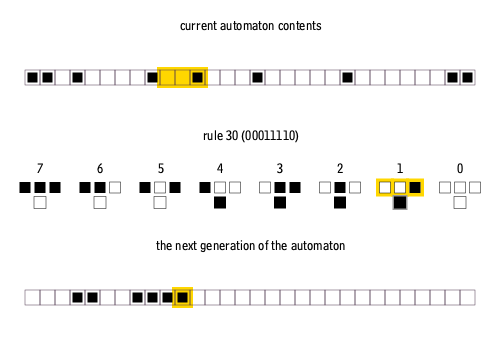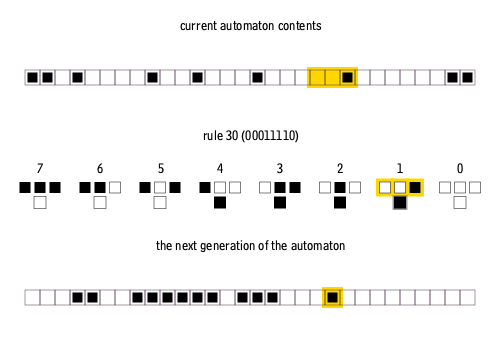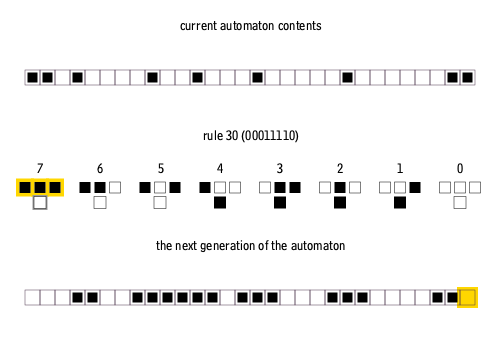
Rule 110
The Rule 110 cellular automaton (often called simply Rule 110) is an elementary cellular automaton with interesting behavior on the boundary between stability and chaos. In this respect, it is similar to Conway's Game of Life. Like Life, Rule 110 with a particular repeating background pattern is known to be Turing complete. This implies that, in principle, any calculation or computer program can be simulated using this automaton. Definition In an elementary cellular automaton, a one-dimensional pattern of 0s and 1s evolves according to a simple set of rules. Whether a point in the pattern will be 0 or 1 in the new generation depends on its current value, as well as on those of its two neighbors. The Rule 110 automaton has the following set of rules: The name "Rule 110" derives from the fact that this rule can be summarized in the binary sequence 01101110; interpreted as a binary number, this corresponds to the decimal value 110. This is the Wolfram code naming scheme. Hi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
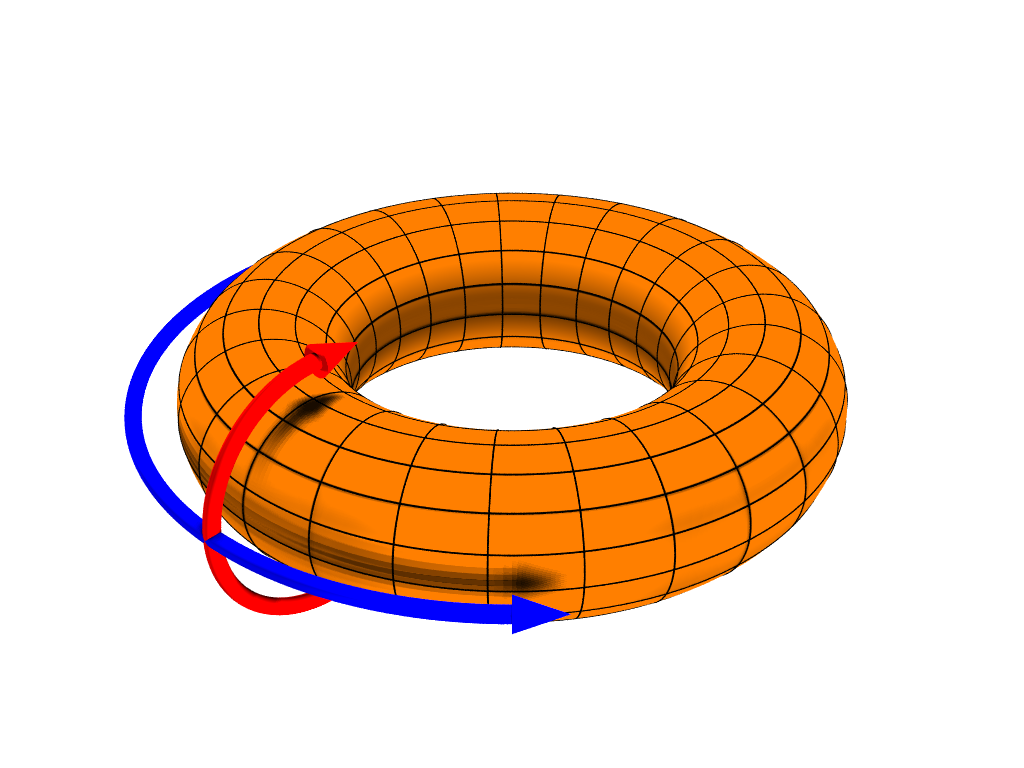
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives. The function is often thought of as an "unknown" that solves the equation, similar to how is thought of as an unknown number solving, e.g., an algebraic equation like . However, it is usually impossible to write down explicit formulae for solutions of partial differential equations. There is correspondingly a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity and stability. Among the many open questions are the existence an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Boundary Condition
Periodic boundary conditions (PBCs) are a set of boundary conditions which are often chosen for approximating a large (infinite) system by using a small part called a ''unit cell''. PBCs are often used in computer simulations and mathematical models. The topology of two-dimensional PBC is equal to that of a ''world map'' of some video games; the geometry of the unit cell satisfies perfect two-dimensional tiling, and when an object passes through one side of the unit cell, it re-appears on the opposite side with the same velocity. In topological terms, the space made by two-dimensional PBCs can be thought of as being mapped onto a torus ( compactification). The large systems approximated by PBCs consist of an infinite number of unit cells. In computer simulations, one of these is the original simulation box, and others are copies called ''images''. During the simulation, only the properties of the original simulation box need to be recorded and propagated. The ''minimum-image conven ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal
In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendicular'' is more specifically used for lines and planes that intersect to form a right angle, whereas ''orthogonal'' is used in generalizations, such as ''orthogonal vectors'' or ''orthogonal curves''. ''Orthogonality'' is also used with various meanings that are often weakly related or not related at all with the mathematical meanings. Etymology The word comes from the Ancient Greek ('), meaning "upright", and ('), meaning "angle". The Ancient Greek (') and Classical Latin ' originally denoted a rectangle. Later, they came to mean a right triangle. In the 12th century, the post-classical Latin word ''orthogonalis'' came to mean a right angle or something related to a right angle. Mathematics Physics Optics In optics, polarization ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Paper
Graph paper, coordinate paper, grid paper, or squared paper is writing paper that is printed with fine lines making up a regular grid. It is available either as loose leaf paper or bound in notebooks or graph books. It is commonly found in mathematics and engineering education settings, exercise books, and in laboratory notebooks. The lines are often used as guides for mathematical notation, plotting graph of a function, graphs of functions or experimental data, and drawing curves. History The Metropolitan Museum of Art owns a pattern book dated to around 1596 in which each page bears a grid woodblock printing, printed with a woodblock. The owner has used these grids to create block pictures in black and white and in colour. The first commercially published "coordinate paper" is usually attributed to a Dr. Buxton of England, who patented paper printed with a rectangular coordinate grid, in 1794. A century later, E. H. Moore, a distinguished mathematician at the University of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Neumann Neighborhood
In cellular automata, the von Neumann neighborhood (or 4-neighborhood) is classically defined on a two-dimensional square lattice and is composed of a central cell and its four adjacent cells. The neighborhood is named after John von Neumann, who used it to define the von Neumann cellular automaton and the von Neumann universal constructor within it. It is one of the two most commonly used neighborhood types for two-dimensional cellular automata, the other one being the Moore neighborhood. This neighbourhood can be used to define the notion of 4-connected pixels in computer graphics.. The von Neumann neighbourhood of a cell is the cell itself and the cells at a Manhattan distance of 1. The concept can be extended to higher dimensions, for example forming a 6-cell octahedral neighborhood for a cubic cellular automaton in three dimensions. Von Neumann neighborhood of range ''r'' An extension of the simple von Neumann neighborhood described above is to take the set of p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moore Neighborhood
In cellular automata, the Moore neighborhood is defined on a two-dimensional square lattice and is composed of a central cell and the eight cells that surround it. Name The neighborhood is named after Edward F. Moore, a pioneer of cellular automata theory. Importance It is one of the two most commonly used neighborhood types, the other one being the von Neumann neighborhood, which excludes the corner cells. The well known Conway's Game of Life, for example, uses the Moore neighborhood. It is similar to the notion of 8-connected pixels in computer graphics. The Moore neighbourhood of a cell is the cell itself and the cells at a Chebyshev distance of 1. The concept can be extended to higher dimensions, for example forming a 26-cell cubic neighborhood for a cellular automaton in three dimensions, as used by 3D Life. In dimension ''d,'' where 0 \le d, d \in \mathbb, the size of the neighborhood is 3''d'' − 1. In two dimensions, the number of cells in an ''ext ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reversible Cellular Automaton
A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The Reversible dynamics, time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood. Several methods are known for defining cellular automata rules that are reversible; these include the block cellular automaton method, in which each update partitions the cells into blocks and applies an invertible function separately to each block, and the second-order cellular automaton method, in which the update rule combines states from two previous steps of the automaton. When ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |