|
Branch Of Mathematics
Mathematics is a broad subject that is commonly divided in many areas or branches that may be defined by their objects of study, by the used methods, or by both. For example, analytic number theory is a subarea of number theory devoted to the use of methods of analysis for the study of natural numbers. This glossary is alphabetically sorted. This hides a large part of the relationships between areas. For the broadest areas of mathematics, see . The Mathematics Subject Classification is a hierarchical list of areas and subjects of study that has been elaborated by the community of mathematicians. It is used by most publishers for classifying mathematical articles and books. A B C D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. Originally called infinitesimal calculus or "the calculus of infinitesimals", it has two major branches, differential calculus and integral calculus. The former concerns instantaneous Rate of change (mathematics), rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus. They make use of the fundamental notions of convergence (mathematics), convergence of infinite sequences and Series (mathematics), infinite series to a well-defined limit (mathematics), limit. It is the "mathematical backbone" for dealing with problems where variables change with time or another reference variable. Infinitesimal calculus was formulated separately ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Insurance
Insurance is a means of protection from financial loss in which, in exchange for a fee, a party agrees to compensate another party in the event of a certain loss, damage, or injury. It is a form of risk management, primarily used to protect against the risk of a contingent or uncertain loss. An entity which provides insurance is known as an insurer, insurance company, insurance carrier, or underwriter. A person or entity who buys insurance is known as a policyholder, while a person or entity covered under the policy is called an insured. The insurance transaction involves the policyholder assuming a guaranteed, known, and relatively small loss in the form of a payment to the insurer (a premium) in exchange for the insurer's promise to compensate the insured in the event of a covered loss. The loss may or may not be financial, but it must be reducible to financial terms. Furthermore, it usually involves something in which the insured has an insurable interest established by o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
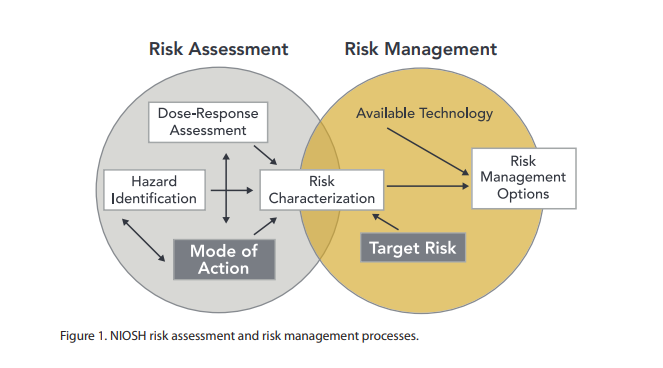
Risk Assessment
Risk assessment is a process for identifying hazards, potential (future) events which may negatively impact on individuals, assets, and/or the environment because of those hazards, their likelihood and consequences, and actions which can mitigate these effects. The output from such a process may also be called a risk assessment. Hazard analysis forms the first stage of a risk assessment process. Judgments "on the tolerability of the risk on the basis of a risk analysis" (i.e. risk evaluation) also form part of the process. The results of a risk assessment process may be expressed in a quantitative or qualitative fashion. Risk assessment forms a key part of a broader risk management strategy to help reduce any potential risk-related consequences. Categories Individual risk assessment Risk assessments can be undertaken in individual cases, including in patient and physician interactions. In the narrow sense chemical risk assessment is the assessment of a health risk in response ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Actuarial Science
Actuarial science is the discipline that applies mathematics, mathematical and statistics, statistical methods to Risk assessment, assess risk in insurance, pension, finance, investment and other industries and professions. Actuary, Actuaries are professionals trained in this discipline. In many countries, actuaries must demonstrate their competence by passing a series of rigorous professional examinations focused in fields such as probability and predictive analysis. Actuarial science includes a number of interrelated subjects, including mathematics, probability theory, statistics, finance, economics, financial accounting and computer science. Historically, actuarial science used deterministic models in the construction of tables and premiums. The science has gone through revolutionary changes since the 1980s due to the proliferation of high speed computers and the union of stochastic actuarial models with modern financial theory. Many universities have undergraduate and gradu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such as Stretch factor, stretching, Torsion (mechanics), twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a Set (mathematics), set endowed with a structure, called a ''Topology (structure), topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of List of continuity-related mathematical topics, continuity. Euclidean spaces, and, more generally, metric spaces are examples of topological spaces, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and Homotopy, homotopies. A property that is invariant under such deformations is a to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Theory
In mathematics, homotopy theory is a systematic study of situations in which Map (mathematics), maps can come with homotopy, homotopies between them. It originated as a topic in algebraic topology, but nowadays is learned as an independent discipline. Applications to other fields of mathematics Besides algebraic topology, the theory has also been used in other areas of mathematics such as: * Algebraic geometry (e.g., A1 homotopy theory, A1 homotopy theory) * Category theory (specifically the study of higher category theory, higher categories) Concepts Spaces and maps In homotopy theory and algebraic topology, the word "space" denotes a topological space. In order to avoid Pathological (mathematics), pathologies, one rarely works with arbitrary spaces; instead, one requires spaces to meet extra constraints, such as being Category of compactly generated weak Hausdorff spaces, compactly generated weak Hausdorff or a CW complex. In the same vein as above, a "Map (mathematics), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Compact Group
In mathematics, a locally compact group is a topological group ''G'' for which the underlying topology is locally compact and Hausdorff. Locally compact groups are important because many examples of groups that arise throughout mathematics are locally compact and such groups have a natural measure called the Haar measure. This allows one to define integrals of Borel measurable functions on ''G'' so that standard analysis notions such as the Fourier transform and L^p spaces can be generalized. Many of the results of finite group representation theory are proved by averaging over the group. For compact groups, modifications of these proofs yields similar results by averaging with respect to the normalized Haar integral. In the general locally compact setting, such techniques need not hold. The resulting theory is a central part of harmonic analysis. The representation theory for locally compact abelian groups is described by Pontryagin duality. Examples and counterexamples *A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Analysis
Harmonic analysis is a branch of mathematics concerned with investigating the connections between a function and its representation in frequency. The frequency representation is found by using the Fourier transform for functions on unbounded domains such as the full real line or by Fourier series for functions on bounded domains, especially periodic functions on finite intervals. Generalizing these transforms to other domains is generally called Fourier analysis, although the term is sometimes used interchangeably with harmonic analysis. Harmonic analysis has become a vast subject with applications in areas as diverse as number theory, representation theory, signal processing, quantum mechanics, tidal analysis, spectral analysis, and neuroscience. The term "harmonics" originated from the Ancient Greek word ''harmonikos'', meaning "skilled in music". In physical eigenvalue problems, it began to mean waves whose frequencies are integer multiples of one another, as are the freq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |