 |
Boundary Value Analysis
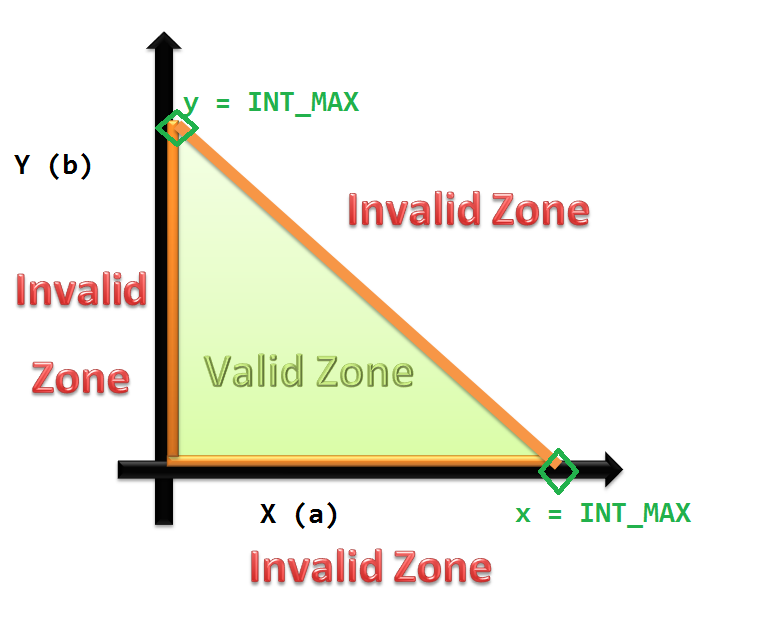
Boundary-value analysis is a software testing technique in which tests are designed to include representatives of boundary values in a range. The idea comes from the boundary. Given that there is a set of test vectors to test the system, a topology can be defined on that set. Those inputs which belong to the same equivalence class as defined by the equivalence partitioning theory would constitute the basis. Given that the basis sets are neighbors, there would exist a boundary between them. The test vectors on either side of the boundary are called boundary values. In practice, this would require that the test vectors can be ordered, and that the individual parameters follows some kind of order (either partial order or total order). Formal definition Formally, the boundary values can be defined as below: :Let the set of the test vectors be . :Let's assume that there is an ordering relation defined over them, as . :Let be two equivalent classes. :Assume that test vector and . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Software Testing
Software testing is the act of checking whether software satisfies expectations. Software testing can provide objective, independent information about the Quality (business), quality of software and the risk of its failure to a User (computing), user or sponsor. Software testing can determine the Correctness (computer science), correctness of software for specific Scenario (computing), scenarios but cannot determine correctness for all scenarios. It cannot find all software bug, bugs. Based on the criteria for measuring correctness from an test oracle, oracle, software testing employs principles and mechanisms that might recognize a problem. Examples of oracles include specifications, Design by Contract, contracts, comparable products, past versions of the same product, inferences about intended or expected purpose, user or customer expectations, relevant standards, and applicable laws. Software testing is often dynamic in nature; running the software to verify actual output ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Boundary (topology)
In topology and mathematics in general, the boundary of a subset of a topological space is the set of points in the Closure (topology), closure of not belonging to the Interior (topology), interior of . An element of the boundary of is called a boundary point of . The term boundary operation refers to finding or taking the boundary of a set. Notations used for boundary of a set include \operatorname(S), \operatorname(S), and \partial S. Some authors (for example Willard, in ''General Topology'') use the term frontier instead of boundary in an attempt to avoid confusion with a Manifold#Manifold with boundary, different definition used in algebraic topology and the theory of manifolds. Despite widespread acceptance of the meaning of the terms boundary and frontier, they have sometimes been used to refer to other sets. For example, ''Metric Spaces'' by E. T. Copson uses the term boundary to refer to Felix Hausdorff, Hausdorff's border, which is defined as the intersection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Artech House
Artech House (a.k.a. Artech House Publishers) is a publisher of professional scientific and engineering books. It is located in London, United Kingdom and Norwood, Massachusetts, United States. Artech House is a subsidiary of Horizon House Publications, Inc. Topics published Artech specializes in books about microwaves and radar, GNSS, power engineering, space engineering, electronic warfare, signal processing Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomograph ..., and other communications-related topics. References External links Artech House US website Artech House UK web site Book publishing companies of the United Kingdom Book publishing companies based in Massachusetts Companies based in Norfolk County, Massachusetts Companies based in the City of Westminster ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Test Vector
In computer science and engineering, a test vector is a set of inputs provided to a system in order to test that system. In software development, test vectors are a methodology of software testing and software verification and validation. Rationale In computer science and engineering, a system acts as a computable function. An example of a specific function could be y = f(x) where y is the output of the system and x is the input; however, most systems' inputs are not one-dimensional. When the inputs are multi-dimensional, we could say that the system takes the form y = f(x_1, x_2, ...) ; however, we can generalize this equation to a general form Y = C(X) where Y is the result of the system's execution, C belongs to the set of computable functions, and X is an input vector. While testing the system, various test vectors must be used to examine the system's behavior with differing inputs. Example For example, consider a login page with two input fields: a username field and a pas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Equivalence Class
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements a and b belong to the same equivalence class if, and only if, they are equivalent. Formally, given a set S and an equivalence relation \sim on S, the of an element a in S is denoted /math> or, equivalently, to emphasize its equivalence relation \sim, and is defined as the set of all elements in S with which a is \sim-related. The definition of equivalence relations implies that the equivalence classes form a partition of S, meaning, that every element of the set belongs to exactly one equivalence class. The set of the equivalence classes is sometimes called the quotient set or the quotient space of S by \sim, and is denoted by S /. When the set S has some structure (such as a group operation or a topology) and the equivalence re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Equivalence Partitioning
Equivalence partitioning or equivalence class partitioning (ECP) is a software testing technique that divides the input data of a software unit into partitions of equivalent data from which test cases can be derived. In principle, test cases are designed to cover each partition at least once. This technique tries to define test cases that uncover classes of errors, thereby reducing the total number of test cases that must be developed. An advantage of this approach is reduction in the time required for testing software due to lesser number of test cases. Equivalence partitioning is typically applied to the inputs of a tested component, but may be applied to the outputs in rare cases. The equivalence partitions are usually derived from the requirements specification for input attributes that influence the processing of the test object. The fundamental concept of ECP comes from equivalence class which in turn comes from equivalence relation. A software system is in effect a comput ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Basis (topology)
In mathematics, a base (or basis; : bases) for the topology of a topological space is a family \mathcal of open subsets of such that every open set of the topology is equal to the union of some sub-family of \mathcal. For example, the set of all open intervals in the real number line \R is a basis for the Euclidean topology on \R because every open interval is an open set, and also every open subset of \R can be written as a union of some family of open intervals. Bases are ubiquitous throughout topology. The sets in a base for a topology, which are called , are often easier to describe and use than arbitrary open sets. Many important topological definitions such as continuity and convergence can be checked using only basic open sets instead of arbitrary open sets. Some topologies have a base of open sets with specific useful properties that may make checking such topological definitions easier. Not all families of subsets of a set X form a base for a topology on X. Under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood (or neighborhood) is one of the basic concepts in a topological space. It is closely related to the concepts of open set and Interior (topology), interior. Intuitively speaking, a neighbourhood of a point is a Set (mathematics), set of points containing that point where one can move some amount in any direction away from that point without leaving the set. Definitions Neighbourhood of a point If X is a topological space and p is a point in X, then a neighbourhood of p is a subset V of X that includes an open set U containing p, p \in U \subseteq V \subseteq X. This is equivalent to the point p \in X belonging to the Interior (topology)#Interior point, topological interior of V in X. The neighbourhood V need not be an open subset of X. When V is open (resp. closed, compact, etc.) in X, it is called an (resp. closed neighbourhood, compact neighbourhood, etc.). Some authors require neighbourhoods to be open, so i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Partial Order
In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word ''partial'' is used to indicate that not every pair of elements needs to be comparable; that is, there may be pairs for which neither element precedes the other. Partial orders thus generalize total orders, in which every pair is comparable. Formally, a partial order is a homogeneous binary relation that is reflexive, antisymmetric, and transitive. A partially ordered set (poset for short) is an ordered pair P=(X,\leq) consisting of a set X (called the ''ground set'' of P) and a partial order \leq on X. When the meaning is clear from context and there is no ambiguity about the partial order, the set X itself is sometimes called a poset. Partial order relations The term ''partial order'' usually refers to the reflexive partial order relations, referred to in this article as ''non-strict'' partial orders. However som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Total Order
In mathematics, a total order or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation \leq on some set X, which satisfies the following for all a, b and c in X: # a \leq a ( reflexive). # If a \leq b and b \leq c then a \leq c ( transitive). # If a \leq b and b \leq a then a = b ( antisymmetric). # a \leq b or b \leq a ( strongly connected, formerly called totality). Requirements 1. to 3. just make up the definition of a partial order. Reflexivity (1.) already follows from strong connectedness (4.), but is required explicitly by many authors nevertheless, to indicate the kinship to partial orders. Total orders are sometimes also called simple, connex, or full orders. A set equipped with a total order is a totally ordered set; the terms simply ordered set, linearly ordered set, toset and loset are also used. The term ''chain'' is sometimes defined as a synonym of ''totally ordered set'', but generally refers to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Fault (technology)
In engineering, a fault is a defect or problem in a system that causes it to fail or act abnormally. An example of this is the Windows fault screen, commonly referred to as the Blue Screen of Death (BSoD). The system actively monitors kernel-mode components. If the system determines that safe system operation is compromised, the system halts to reduce further damage. The ISO document 10303-226 defines ''fault'' as an abnormal condition or defect at the component, equipment, or sub-system level which may lead to a failure. The United States Glossary of Telecommunication Terms defines ''fault'' for telecommunications as: #An accidental condition that causes a functional unit to fail to perform its required function. See#A defect that causes a reproducible or catastrophic malfunction. A malfunction is considered reproducible if it occurs consistently under the same circumstances. See . # In Electric power, power systems, an unintentional short circuit, or partial short circuit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Test Case
In software engineering, a test case is a specification of the inputs, execution conditions, testing procedure, and expected results that define a single test to be executed to achieve a particular software testing objective, such as to exercise a particular program path or to verify compliance with a specific requirement. Test cases underlie testing that is methodical rather than haphazard. A battery of test cases can be built to produce the desired coverage of the software being tested. Formally defined test cases allow the same tests to be run repeatedly against successive versions of the software, allowing for effective and consistent regression testing. Formal test cases In order to fully test that all the requirements of an application are met, there must be at least two test cases for each requirement: one positive test and one negative test. If a requirement has sub-requirements, each sub-requirement must have at least two test cases. Keeping track of the link between ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |