|
Best Response
In game theory, the best response is the strategy (or strategies) which produces the most favorable outcome for a player, taking other players' strategies as given. The concept of a best response is central to John Nash's best-known contribution, the Nash equilibrium, the point at which each player in a game has selected the best response (or one of the best responses) to the other players' strategies. Correspondence Reaction correspondences, also known as best response correspondences, are used in the proof of the existence of mixed strategy Nash equilibria. Reaction correspondences are not "reaction functions" since functions must only have one value per argument, and many reaction correspondences will be undefined, i.e., a vertical line, for some opponent strategy choice. One constructs a correspondence , for each player from the set of opponent strategy profiles into the set of the player's strategies. So, for any given set of opponent's strategies , represents player ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed two-person zero-sum games, in which a participant's gains or losses are exactly balanced by the losses and gains of the other participant. In the 1950s, it was extended to the study of non zero-sum games, and was eventually applied to a wide range of Human behavior, behavioral relations. It is now an umbrella term for the science of rational Decision-making, decision making in humans, animals, and computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics. His paper was f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
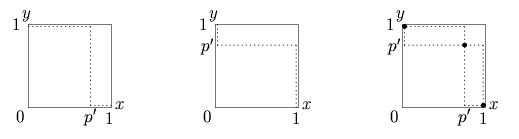
Independent Variable
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, on the other hand, are not seen as depending on any other variable in the scope of the experiment in question. Rather, they are controlled by the experimenter. In pure mathematics In mathematics, a function is a rule for taking an input (in the simplest case, a number or set of numbers)Carlson, Robert. A concrete introduction to real analysis. CRC Press, 2006. p.183 and providing an output (which may also be a number). A symbol that stands for an arbitrary input is called an independent variable, while a symbol that stands for an arbitrary output is called a dependent variable. The most common symbol for the input is , and the most common symbol for the output is ; the function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prisoner's Dilemma
The prisoner's dilemma is a game theory thought experiment involving two rational agents, each of whom can either cooperate for mutual benefit or betray their partner ("defect") for individual gain. The dilemma arises from the fact that while defecting is rational for each agent, cooperation yields a higher payoff for each. The puzzle was designed by Merrill Flood and Melvin Dresher in 1950 during their work at the RAND Corporation. They invited economist Armen Alchian and mathematician John Williams to play a hundred rounds of the game, observing that Alchian and Williams often chose to cooperate. When asked about the results, John_Forbes_Nash_Jr., John Nash remarked that rational behavior in the Prisoner's dilemma#The_iterated_prisoner's_dilemma, iterated version of the game can differ from that in a single-round version. This insight anticipated a Folk_theorem_(game_theory), key result in game theory: cooperation can emerge in repeated interactions, even in situations where it i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dominance (game Theory)
In game theory, a strategy ''A'' dominates another strategy ''B'' if ''A'' will always produce a better result than ''B'', regardless of how any other player plays. Some very simple games (called straightforward games) can be solved using dominance. Terminology A player can compare two strategies, A and B, to determine which one is better. The result of the comparison is one of: * B strictly dominates (>) A: choosing B always gives a better outcome than choosing A, no matter what the other players do. * B weakly dominates (≥) A: choosing B always gives at least as good an outcome as choosing A, no matter what the other players do, and there is at least one set of opponents' actions for which B gives a better outcome than A. (Notice that if B strictly dominates A, then B weakly dominates A. Therefore, we can say "B dominates A" to mean "B weakly dominates A".) * B is weakly dominated by A: there is at least one set of opponents' actions for which B gives a worse outcome than A, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncorrelated Asymmetry
In game theory, an uncorrelated asymmetry is an arbitrary distinguishing feature between players in an otherwise symmetric game. This concept refers to asymmetries that are unrelated to the Payoff matrix, payoffs or strategic structure of the game itself, but instead arise from players' ability to distinguish their roles or identities within the game. It is opposed to correlated asymmetries, where the asymmetry directly affects payoffs or strategic considerations. The term was introduced by John Maynard Smith in 1973. For example, consider two drivers approaching each other on a narrow road where only one can pass at a time. The payoffs are symmetric—both prefer that one yields while the other proceeds rather than both attempting to proceed simultaneously. However, if one driver arrived first or is driving on the "right" side according to local convention, this creates an uncorrelated asymmetry that can guide their strategies without changing the underlying payoff structure. The k ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evolutionarily Stable Strategy
An evolutionarily stable strategy (ESS) is a strategy (or set of strategies) that is ''impermeable'' when adopted by a population in adaptation to a specific environment, that is to say it cannot be displaced by an alternative strategy (or set of strategies) which may be novel or initially rare. Introduced by John Maynard Smith and George R. Price in 1972/3, it is an important concept in behavioural ecology, evolutionary psychology, mathematical game theory and economics, with applications in other fields such as anthropology, philosophy and political science. In game-theoretical terms, an ESS is an equilibrium refinement of the Nash equilibrium, being a Nash equilibrium that is also "evolutionarily stable." Thus, once fixed in a population, natural selection alone is sufficient to prevent alternative ( mutant) strategies from replacing it (although this does not preclude the possibility that a better strategy, or set of strategies, will emerge in response to selective press ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hawk-dove Game
The game of chicken, also known as the hawk-dove game or snowdrift game, is a model of conflict for two players in game theory. The principle of the game is that while the ideal outcome is for one player to yield (to avoid the worst outcome if neither yields), individuals try to avoid it out of pride, not wanting to look like "chickens". Each player taunts the other to increase the risk of shame in yielding. However, when one player yields, the conflict is avoided, and the game essentially ends. The name "chicken" has its origins in a game in which two drivers drive toward each other on a collision course: one must swerve, or both may die in the crash, but if one driver swerves and the other does not, the one who swerved will be called a "chicken", meaning a coward; this terminology is most prevalent in political science and economics. The name "hawk–dove" refers to a situation in which there is a competition for a shared resource and the contestants can choose either conciliat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
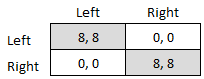
Coordination Game
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibrium, Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Battle Of The Sexes (game Theory)
In game theory, the battle of the sexes is a two-player coordination game that also involves elements of conflict. The game was introduced in 1957 by R. Duncan Luce and Howard Raiffa in their classic book, ''Games and Decisions''. Some authors prefer to avoid assigning sexes to the players and instead use Players 1 and 2, and some refer to the game as Bach or Stravinsky, using two concerts as the two events.Osborne, Martin and Ariel Rubinstein (1994). ''A Course in Game Theory.'' The MIT Press. The game description here follows Luce and Raiffa's original story. Imagine that a man and a woman hope to meet this evening, but have a choice between two events to attend: a prize fight and a ballet. The man would prefer to go to prize fight. The woman would prefer the ballet. Both would prefer to go to the same event rather than different ones. If they cannot communicate, where should they go? The payoff matrix labeled "Battle of the Sexes (1)" shows the payoffs when the man cho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |