|
Batch Normalization
Batch normalization (also known as batch norm) is a normalization technique used to make training of artificial neural networks faster and more stable by adjusting the inputs to each layer—re-centering them around zero and re-scaling them to a standard size. It was introduced by Sergey Ioffe and Christian Szegedy in 2015. Experts still debate why batch normalization works so well. It was initially thought to tackle ''internal covariate shift'', a problem where parameter initialization and changes in the distribution of the inputs of each layer affect the learning rate of the network. However, newer research suggests it doesn’t fix this shift but instead smooths the objective function—a mathematical guide the network follows to improve—enhancing performance. In very deep networks, batch normalization can initially cause a severe gradient explosion—where updates to the network grow uncontrollably large—but this is managed with shortcuts called skip connections in resi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normalization (machine Learning)
In machine learning, normalization is a statistical technique with various applications. There are two main forms of normalization, namely ''data normalization'' and ''activation normalization''. Data normalization (or feature scaling) includes methods that rescale input data so that the features have the same range, mean, variance, or other statistical properties. For instance, a popular choice of feature scaling method is min-max normalization, where each feature is transformed to have the same range (typically ,1/math> or 1,1/math>). This solves the problem of different features having vastly different scales, for example if one feature is measured in kilometers and another in nanometers. Activation normalization, on the other hand, is specific to deep learning, and includes methods that rescale the activation of hidden neurons inside neural networks. Normalization is often used to: * increase the speed of training convergence, * reduce sensitivity to variations and feat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent And Identically Distributed Random Variables
Independent or Independents may refer to: Arts, entertainment, and media Artist groups * Independents (artist group), a group of modernist painters based in Pennsylvania, United States * Independentes (English: Independents), a Portuguese artist group Music Groups, labels, and genres * Independent music, a number of genres associated with independent labels * Independent record label, a record label not associated with a major label * Independent Albums, American albums chart Albums * ''Independent'' (Ai album), 2012 * ''Independent'' (Faze album), 2006 * ''Independent'' (Sacred Reich album), 1993 Songs * "Independent" (song), a 2007 song by Webbie * "Independent", a 2002 song by Ayumi Hamasaki from '' H'' News media organizations * Independent Media Center (also known as Indymedia or IMC), an open publishing network of journalist collectives that report on political and social issues, e.g., in ''The Indypendent'' newspaper of NYC * ITV (TV network) (Independent Televi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bisection Algorithm
In mathematics, the bisection method is a root-finding method that applies to any continuous function for which one knows two values with opposite signs. The method consists of repeatedly bisecting the interval defined by these values and then selecting the subinterval in which the function changes sign, and therefore must contain a root. It is a very simple and robust method, but it is also relatively slow. Because of this, it is often used to obtain a rough approximation to a solution which is then used as a starting point for more rapidly converging methods. The method is also called the interval halving method, the binary search method, or the dichotomy method. For polynomials, more elaborate methods exist for testing the existence of a root in an interval (Descartes' rule of signs, Sturm's theorem, Budan's theorem). They allow extending the bisection method into efficient algorithms for finding all real roots of a polynomial; see Real-root isolation. The method The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient Descent
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for minimizing a differentiable multivariate function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a trajectory that maximizes that function; the procedure is then known as ''gradient ascent''. It is particularly useful in machine learning for minimizing the cost or loss function. Gradient descent should not be confused with local search algorithms, although both are iterative methods for optimization. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
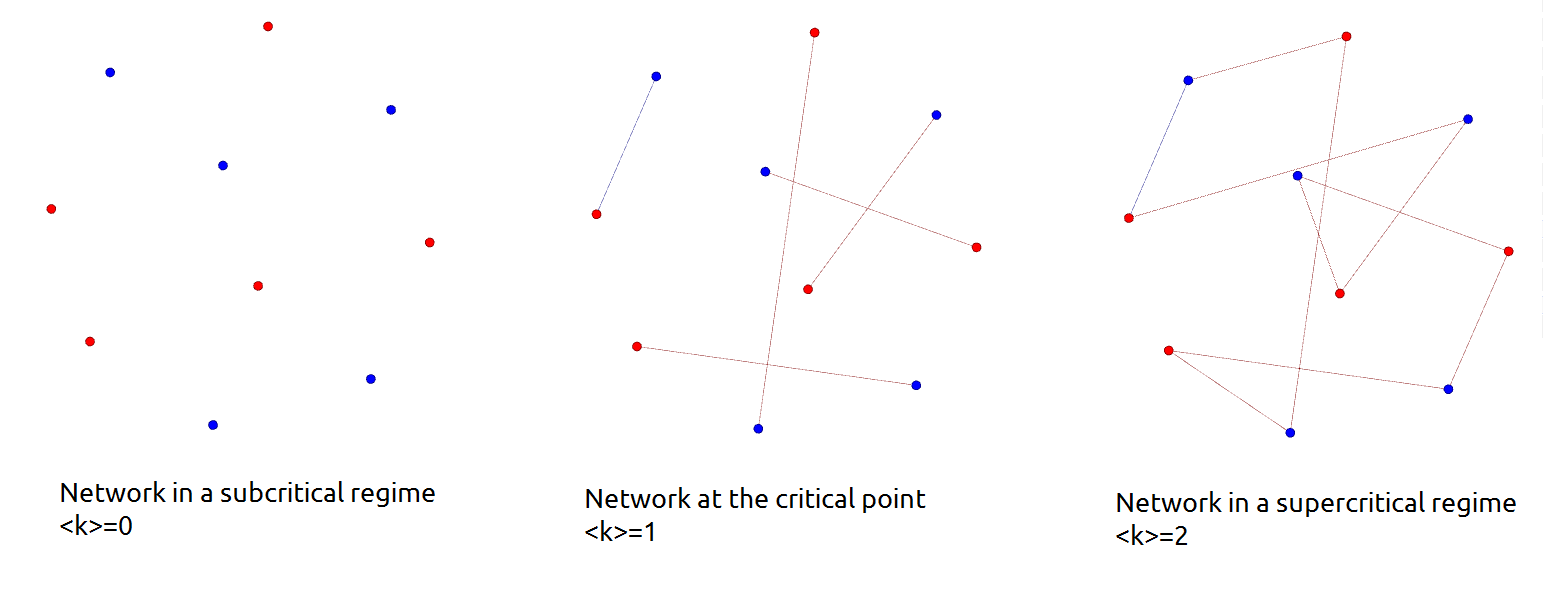
Critical Point (network Science)
In network science, a critical point is a value of average degree, which separates random networks that have a giant component from those that do not (i.e. it separates a network in a subcritical regime from one in a supercritical regime). Considering a random network with an average degree \langle k\rangle the critical point is \langle k\rangle = 1 where the average degree is defined by the fraction of the number of edges (e) and nodes (N) in the network, that is \langle k\rangle =\frac. Subcritical regime In a subcritical regime the network has no giant component, only small clusters. In the special case of \langle k\rangle =0 the network is not connected at all. A random network is in a subcritical regime until the average degree exceeds the critical point, that is the network is in a subcritical regime as long as \langle k\rangle 1. Example on different regimes Consider a speed dating event as an example, with the participants as the nodes of the network. At the begi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables, each of which clusters around a mean value. Definitions Notation and parametrization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that \mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smoothness
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives (''differentiability class)'' it has over its domain. A function of class C^k is a function of smoothness at least ; that is, a function of class C^k is a function that has a th derivative that is continuous in its domain. A function of class C^\infty or C^\infty-function (pronounced C-infinity function) is an infinitely differentiable function, that is, a function that has derivatives of all orders (this implies that all these derivatives are continuous). Generally, the term smooth function refers to a C^-function. However, it may also mean "sufficiently differentiable" for the problem under consideration. Differentiability classes Differentiability class is a classification of functions according to the properties of their derivatives. It is a measure of the highest order of derivative that exists and is continuous for a function. Consider an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perceptron
In machine learning, the perceptron is an algorithm for supervised classification, supervised learning of binary classification, binary classifiers. A binary classifier is a function that can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of Weighting, weights with the feature vector. History The artificial neuron network was invented in 1943 by Warren McCulloch and Walter Pitts in ''A Logical Calculus of the Ideas Immanent in Nervous Activity, A logical calculus of the ideas immanent in nervous activity''. In 1957, Frank Rosenblatt was at the Cornell Aeronautical Laboratory. He simulated the perceptron on an IBM 704. Later, he obtained funding by the Information Systems Branch of the United States Office of Naval Research and the Rome Air Development Center, to build a custom- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative or complex number). Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation rotates, stretches, or shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with neither rotation nor shear. The corresponding eigenvalue is the factor by which an eigenvector is stretched or shrunk. If the eigenvalue is negative, the eigenvector's direction is reversed. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rayleigh Quotient
In mathematics, the Rayleigh quotient () for a given complex Hermitian matrix M and nonzero vector ''x'' is defined as:R(M,x) = .For real matrices and vectors, the condition of being Hermitian reduces to that of being symmetric, and the conjugate transpose x^ to the usual transpose x'. Note that R(M, c x) = R(M,x) for any non-zero scalar ''c''. Recall that a Hermitian (or real symmetric) matrix is diagonalizable with only real eigenvalues. It can be shown that, for a given matrix, the Rayleigh quotient reaches its minimum value \lambda_\min (the smallest eigenvalue of ''M'') when ''x'' is v_\min (the corresponding eigenvector). Similarly, R(M, x) \leq \lambda_\max and R(M, v_\max) = \lambda_\max. The Rayleigh quotient is used in the min-max theorem to get exact values of all eigenvalues. It is also used in eigenvalue algorithms (such as Rayleigh quotient iteration) to obtain an eigenvalue approximation from an eigenvector approximation. The range of the Rayleigh quotient (fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Definiteness
In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular: * Positive-definite bilinear form * Positive-definite function * Positive-definite function on a group * Positive-definite functional * Positive-definite kernel * Positive-definite matrix In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. Mo ... * Positive-definite operator * Positive-definite quadratic form References *. *. {{Set index article, mathematics Quadratic forms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Semidefinite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number \mathbf^* M \mathbf is positive for every nonzero complex column vector \mathbf, where \mathbf^* denotes the conjugate transpose of \mathbf. Positive semi-definite matrices are defined similarly, except that the scalars \mathbf^\mathsf M \mathbf and \mathbf^* M \mathbf are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called ''indefinite''. Some authors use more general definitions of definiteness, permitting the matrices to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |