|
Baby-step Giant-step
In group theory, a branch of mathematics, the baby-step giant-step is a meet-in-the-middle algorithm for computing the discrete logarithm or order of an element in a finite abelian group by Daniel Shanks. The discrete log problem is of fundamental importance to the area of public key cryptography. Many of the most commonly used cryptography systems are based on the assumption that the discrete log is extremely difficult to compute; the more difficult it is, the more security it provides a data transfer. One way to increase the difficulty of the discrete log problem is to base the cryptosystem on a larger group. Theory The algorithm is based on a space–time tradeoff. It is a fairly simple modification of trial multiplication, the naive method of finding discrete logarithms. Given a cyclic group G of order n, a generator \alpha of the group and a group element \beta, the problem is to find an integer x such that : \alpha^x = \beta\,. The baby-step giant-step algorithm is based ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Group Theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field (mathematics), fields, and vector spaces, can all be seen as groups endowed with additional operation (mathematics), operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right. Various physical systems, such as crystals and the hydrogen atom, and Standard Model, three of the four known fundamental forces in the universe, may be modelled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also cen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hash Table
In computer science, a hash table is a data structure that implements an associative array, also called a dictionary or simply map; an associative array is an abstract data type that maps Unique key, keys to Value (computer science), values. A hash table uses a hash function to compute an ''index'', also called a ''hash code'', into an array of ''buckets'' or ''slots'', from which the desired value can be found. During lookup, the key is hashed and the resulting hash indicates where the corresponding value is stored. A map implemented by a hash table is called a hash map. Most hash table designs employ an Perfect hash function, imperfect hash function. Hash collision, Hash collisions, where the hash function generates the same index for more than one key, therefore typically must be accommodated in some way. In a well-dimensioned hash table, the average time complexity for each lookup is independent of the number of elements stored in the table. Many hash table designs also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Group Theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field (mathematics), fields, and vector spaces, can all be seen as groups endowed with additional operation (mathematics), operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right. Various physical systems, such as crystals and the hydrogen atom, and Standard Model, three of the four known fundamental forces in the universe, may be modelled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also cen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Andrew Sutherland (mathematician)
Andrew Victor Sutherland is an American mathematician and Senior Research Scientist at the Massachusetts Institute of Technology. His research focuses on computational aspects of number theory and arithmetic geometry. He is known for his contributions to several projects involving large scale computations, including the Polymath project on bounded gaps between primes, the L-functions and Modular Forms Database, the sums of three cubes project, and the computation and classification of Sato-Tate distributions. Education and career Sutherland earned a bachelor's degree in mathematics from MIT in 1990. Following an entrepreneurial career in the software industry he returned to MIT and completed his doctoral degree in mathematics in 2007 under the supervision of Michael Sipser and Ronald Rivest, winning the George M. Sprowls prize for his thesis. He joined the MIT mathematics department as a Research Scientist in 2009. He was promoted to Principal Research Scientist in 2012, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Henri Cohen (number Theorist)
Henri Cohen may refer to: * Henri Cohen (composer) (1808–1880), French music theorist and composer * Henri Cohen (water polo) (died 1930), Belgian water polo athlete * Henri Cohen (number theorist) (born 1947), French mathematician See also * Henry Cohen (other) {{hndis, Cohen, Henri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Alexander Gelfond
Alexander Osipovich Gelfond (; 24October 19067November 1968) was a Soviet mathematician. Gelfond's theorem, also known as the Gelfond–Schneider theorem, is named after him. Biography Alexander Gelfond was born in Saint Petersburg, Russian Empire, the son of a professional physician and amateur philosopher Osip Gelfond. He entered Moscow State University in 1924, started his postgraduate studies there in 1927, and obtained his Ph.D. in 1930. His advisors were Aleksandr Khinchin (1894-1959) and Vyacheslav Stepanov (1889-1950). In 1930, he stayed for five months in Germany (in Berlin and Göttingen) where he worked with Edmund Landau, Carl Ludwig Siegel, and David Hilbert. In 1931 he started teaching as a Professor at the Moscow State University and worked there until the last day of his life. Since 1933 he also worked at the Steklov Institute of Mathematics. In 1939, he was elected a Corresponding member of the Academy of Sciences of the Soviet Union for his works in the f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pollard's Rho Algorithm For Logarithms
Pollard's rho algorithm for logarithms is an algorithm introduced by John Pollard in 1978 to solve the discrete logarithm problem, analogous to Pollard's rho algorithm to solve the integer factorization problem. The goal is to compute \gamma such that \alpha ^ \gamma = \beta, where \beta belongs to a cyclic group G generated by \alpha. The algorithm computes integers a, b, A, and B such that \alpha^a \beta^b = \alpha^A \beta^B. If the underlying group is cyclic of order n, by substituting \beta as ^ and noting that two powers are equal if and only if the exponents are equivalent modulo the order of the base, in this case modulo n, we get that \gamma is one of the solutions of the equation (B-b) \gamma = (a-A) \pmod n. Solutions to this equation are easily obtained using the extended Euclidean algorithm. To find the needed a, b, A, and B the algorithm uses Floyd's cycle-finding algorithm to find a cycle in the sequence x_i = \alpha^ \beta^, where the function f: x_i \mapsto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pohlig–Hellman Algorithm
In group theory, the Pohlig–Hellman algorithm, sometimes credited as the Silver–Pohlig–Hellman algorithm,#Mollin06, Mollin 2006, pg. 344 is a special-purpose algorithm for computing discrete logarithms in a finite abelian group whose order is a smooth integer. The algorithm was introduced by Roland Silver, but first published by Stephen Pohlig and Martin Hellman, who credit Silver with its earlier independent but unpublished discovery. Pohlig and Hellman also list Richard Schroeppel and H. Block as having found the same algorithm, later than Silver, but again without publishing it. Groups of prime-power order As an important special case, which is used as a subroutine in the general algorithm (see below), the Pohlig–Hellman algorithm applies to Group (mathematics), groups whose order is a prime power. The basic idea of this algorithm is to iteratively compute the p-adic digits of the logarithm by repeatedly "shifting out" all but one unknown digit in the exponent, and co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
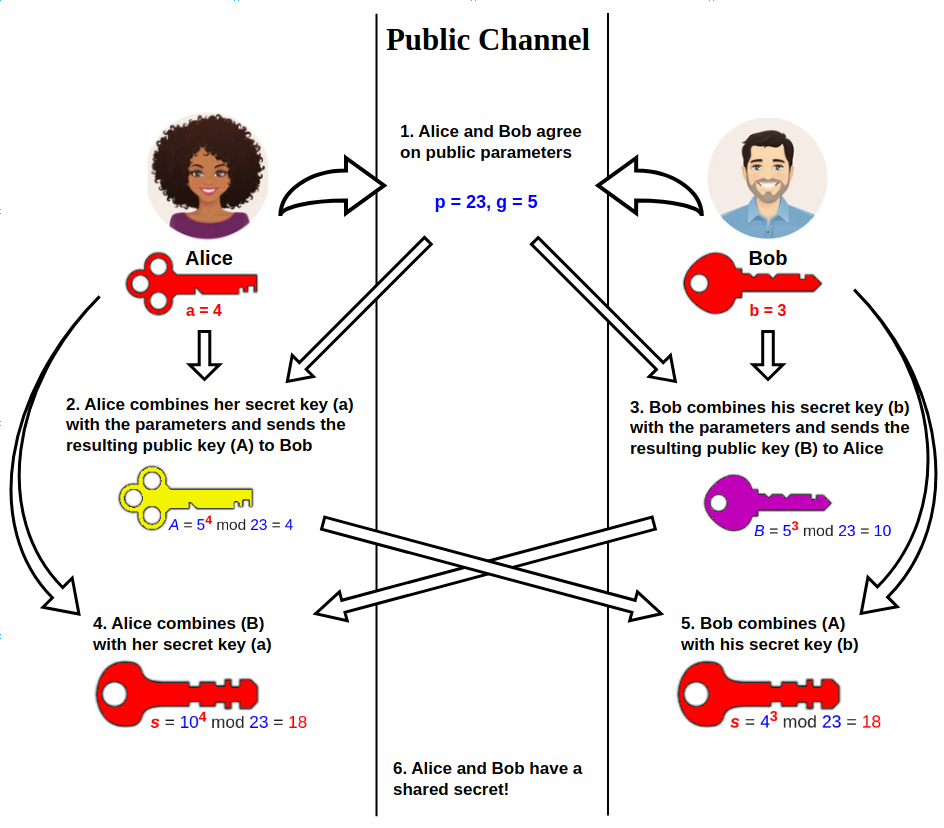
Diffie–Hellman Key Exchange
Diffie–Hellman (DH) key exchangeSynonyms of Diffie–Hellman key exchange include: * Diffie–Hellman–Merkle key exchange * Diffie–Hellman key agreement * Diffie–Hellman key establishment * Diffie–Hellman key negotiation * Exponential key exchange * Diffie–Hellman protocol * Diffie–Hellman handshake is a mathematical method of securely generating a symmetric cryptographic key over a public channel and was one of the first public-key protocols as conceived by Ralph Merkle and named after Whitfield Diffie and Martin Hellman. DH is one of the earliest practical examples of public key exchange implemented within the field of cryptography. Published in 1976 by Diffie and Hellman, this is the earliest publicly known work that proposed the idea of a private key and a corresponding public key. Traditionally, secure encrypted communication between two parties required that they first exchange keys by some secure physical means, such as paper key lists transported by a tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Big O Notation
Big ''O'' notation is a mathematical notation that describes the asymptotic analysis, limiting behavior of a function (mathematics), function when the Argument of a function, argument tends towards a particular value or infinity. Big O is a member of a #Related asymptotic notations, family of notations invented by German mathematicians Paul Gustav Heinrich Bachmann, Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for '':wikt:Ordnung#German, Ordnung'', meaning the order of approximation. In computer science, big O notation is used to Computational complexity theory, classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetic function, arithmetical function and a better understood approximation; one well-known exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Generating Set Of A Group
In abstract algebra, a generating set of a group is a subset of the group set such that every element of the group (mathematics), group can be expressed as a combination (under the group operation) of finitely many elements of the subset and their Inverse element, inverses. In other words, if S is a subset of a group G, then \langle S\rangle, the ''subgroup generated by S'', is the smallest subgroup of G containing every element of S, which is equal to the intersection over all subgroups containing the elements of S; equivalently, \langle S\rangle is the subgroup of all elements of G that can be expressed as the finite product of elements in S and their inverses. (Note that inverses are only needed if the group is infinite; in a finite group, the inverse of an element can be expressed as a power of that element.) If G=\langle S\rangle, then we say that S ''generates'' G, and the elements in S are called ''generators'' or ''group generators''. If S is the empty set, then \langle S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Meet-in-the-middle Attack
The meet-in-the-middle attack (MITM), a known-plaintext attack, is a generic space–time tradeoff cryptographic attack against encryption schemes that rely on performing multiple encryption operations in sequence. The MITM attack is the primary reason why Double DES is not used and why a Triple DES key (168-bit) can be brute-forced by an attacker with 256 space and 2112 operations. Description When trying to improve the security of a block cipher, a tempting idea is to encrypt the data several times using multiple keys. One might think this doubles or even ''n''-tuples the security of the multiple-encryption scheme, depending on the number of times the data is encrypted, because an exhaustive search on all possible combinations of keys (simple brute force) would take 2''n''·''k'' attempts if the data is encrypted with ''k''-bit keys ''n'' times. The MITM attack is a generic attack which weakens the security benefits of using multiple encryptions by storing intermediate value ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |