|
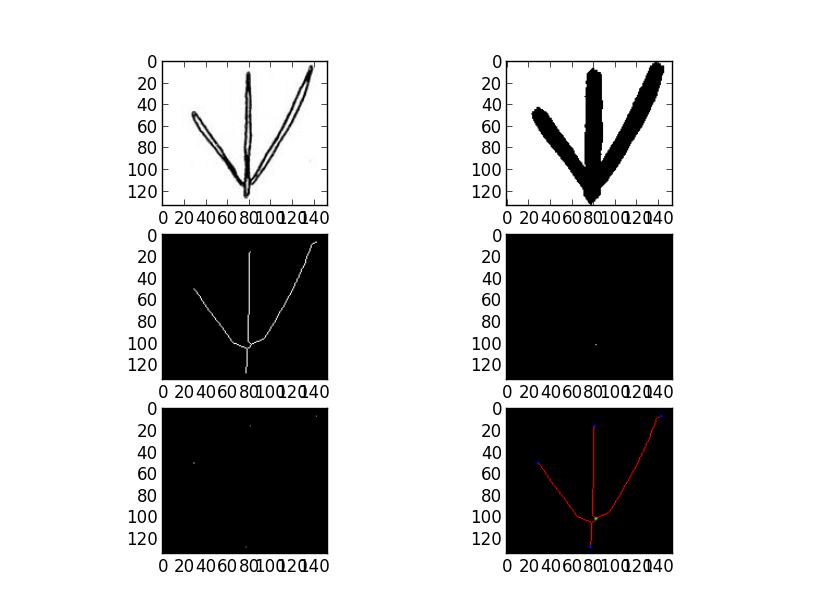
Thinning (morphology)
Thinning is the transformation of a digital image into a simplified, but topologically equivalent image. It is a type of topological skeleton, but computed using mathematical morphology operators. Example Let E=Z^2, and consider the eight composite structuring elements, composed by: :C_1=\ and D_1=\, :C_2=\ and D_2=\ and the three rotations of each by 90^o, 180^o, and 270^o. The corresponding composite structuring elements are denoted B_1,\ldots,B_8. For any ''i'' between 1 and 8, and any binary image ''X'', define ::X\otimes B_i=X\setminus (X\odot B_i), where \setminus denotes the set-theoretical difference and \odot denotes the hit-or-miss transform. The thinning of an image ''A'' is obtained by cyclically iterating until convergence: :A\otimes B_1\otimes B_2\otimes\ldots\otimes B_8\otimes B_1\otimes B_2\otimes\ldots. Thickening Thickening is the dual of thinning that is used to grow selected regions of foreground pixels. In most cases in image processing thickening i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Image
A digital image is an image composed of picture elements, also known as pixels, each with '' finite'', '' discrete quantities'' of numeric representation for its intensity or gray level that is an output from its two-dimensional functions fed as input by its spatial coordinates denoted with ''x'', ''y'' on the x-axis and y-axis, respectively. An image can be vector or raster type. By itself, the term "digital image" usually refers to raster images or bitmapped images (as opposed to vector images). Raster Raster images have a finite set of digital values, called ''picture elements'' or pixels. The digital image contains a fixed number of rows and columns of pixels. Pixels are the smallest individual element in an image, holding quantized values that represent the brightness of a given color at any specific point. Typically, the pixels are stored in computer memory as a raster image or raster map, a two-dimensional array of small integers. These values are often trans ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Skeleton
In shape analysis, skeleton (or topological skeleton) of a shape is a thin version of that shape that is equidistant to its boundaries. The skeleton usually emphasizes geometrical and topological properties of the shape, such as its connectivity, topology, length, direction, and width. Together with the distance of its points to the shape boundary, the skeleton can also serve as a representation of the shape (they contain all the information necessary to reconstruct the shape). Skeletons have several different mathematical definitions in the technical literature, and there are many different algorithms for computing them. Various different variants of skeleton can also be found, including straight skeletons, morphological skeletons, etc. In the technical literature, the concepts of skeleton and medial axis are used interchangeably by some authors,, Section 11.1.5, p. 650 while some other authors, Section 9.9, p. 382., Section 17.5.2, p. 234. regard them as re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Morphology
Mathematical morphology (MM) is a theory and technique for the analysis and processing of Geometry, geometrical structures, based on set theory, lattice theory, topology, and random functions. MM is most commonly applied to digital images, but it can be employed as well on Graph (discrete mathematics), graphs, polygon mesh, surface meshes, Solid geometry, solids, and many other spatial structures. Topology, Topological and Geometry, geometrical continuum (theory), continuous-space concepts such as size, shape, convex set, convexity, Connectedness, connectivity, and geodesic distance, were introduced by MM on both continuous and discrete spaces. MM is also the foundation of morphological image processing, which consists of a set of operators that transform images according to the above characterizations. The basic morphological operators are Erosion (morphology), erosion, Dilation (morphology), dilation, Opening (morphology), opening and Closing (morphology), closing. MM was orig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Minus
In set theory, the complement of a set , often denoted by A^c (or ), is the set of elements not in . When all elements in the universe, i.e. all elements under consideration, are considered to be members of a given set , the absolute complement of is the set of elements in that are not in . The relative complement of with respect to a set , also termed the set difference of and , written B \setminus A, is the set of elements in that are not in . Absolute complement Definition If is a set, then the absolute complement of (or simply the complement of ) is the set of elements not in (within a larger set that is implicitly defined). In other words, let be a set that contains all the elements under study; if there is no need to mention , either because it has been previously specified, or it is obvious and unique, then the absolute complement of is the relative complement of in : A^c= U \setminus A = \. The absolute complement of is usually denoted by A^c. Other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hit-or-miss Transform
In mathematical morphology, hit-or-miss transform is an operation that detects a given configuration (or pattern) in a binary image, using the morphological erosion (morphology), erosion operator and a pair of Disjoint sets, disjoint structuring elements. The result of the hit-or-miss transform is the set of positions where the first structuring element fits in the foreground of the input image, and the second structuring element misses it completely. Mathematical definition In binary morphology, an image is viewed as a subset of a Euclidean space \mathbb^d or the integer grid \mathbb^d, for some dimension ''d''. Let us denote this space or grid by ''E''. A structuring element is a simple, pre-defined shape, represented as a binary image, used to probe another binary image, in morphological operations such as erosion (morphology), erosion, dilation (morphology), dilation, opening (morphology), opening, and closing (morphology), closing. Let C and D be two structuring elements ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Morphology
Mathematical morphology (MM) is a theory and technique for the analysis and processing of Geometry, geometrical structures, based on set theory, lattice theory, topology, and random functions. MM is most commonly applied to digital images, but it can be employed as well on Graph (discrete mathematics), graphs, polygon mesh, surface meshes, Solid geometry, solids, and many other spatial structures. Topology, Topological and Geometry, geometrical continuum (theory), continuous-space concepts such as size, shape, convex set, convexity, Connectedness, connectivity, and geodesic distance, were introduced by MM on both continuous and discrete spaces. MM is also the foundation of morphological image processing, which consists of a set of operators that transform images according to the above characterizations. The basic morphological operators are Erosion (morphology), erosion, Dilation (morphology), dilation, Opening (morphology), opening and Closing (morphology), closing. MM was orig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |