|
Zeisel Number
A Zeisel number, named after Helmut Zeisel, is a square-free integer ''k'' with at least three prime factors which fall into the pattern :p_x = ap_ + b where ''a'' and ''b'' are some integer constants and ''x'' is the index number of each prime factor in the factorization, sorted from lowest to highest. For the purpose of determining Zeisel numbers, p_0 = 1. The first few Zeisel numbers are :105, 1419, 1729, 1885, 4505, 5719, 15387, 24211, 25085, 27559, 31929, 54205, 59081, 114985, 207177, 208681, 233569, 287979, 294409, 336611, 353977, 448585, 507579, 982513, 1012121, 1073305, 1242709, 1485609, 2089257, 2263811, 2953711, … . To give an example, 1729 is a Zeisel number with the constants ''a'' = 1 and ''b'' = 6, its factors being 7, 13 and 19, falling into the pattern : \begin p_1 = 7, & \quad p_1 = 1p_0 + 6 \\ p_2 = 13, & \quad p_2 = 1p_1 + 6 \\ p_3 = 19, & \quad p_3 = 1p_2 + 6 \end 1729 is an example for Carmichael numbers of the kind (6n + 1)(12n + 1)(18n + 1), which satisf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmut Zeisel
Helmut is a German name. Variants include Hellmut, Helmuth, and Hellmuth. From old German, the first element deriving from either ''heil'' ("healthy") or ''hiltja'' ("battle"), and the second from ''muot'' ("spirit, mind, mood"). Helmut may refer to: People A–L *Helmut Angula (born 1945), Namibian politician *Helmut Ashley (1919–2021), Austrian director and cinematographer *Helmut Bakaitis (born 1944), Australian director and actor *Helmut Berger (born 1944), Austrian actor *Helmut Dantine (1917–1982), Austrian actor *Helmut Deutsch (born 1945), Austrian classical pianist *Helmut Ditsch (born 1962), Argentine painter *Hellmut Diwald (1924–1993), German historian *Helmut Donner (born 1941), Austrian high jumper *Helmut Fischer (1926–1997), German actor *Hellmut von Gerlach (1866–1935), German journalist * Helmut Goebbels (1935–1945), only son of Joseph Goebbels *Helmut Griem (1932–2004), German actor *Helmut Gröttrup (1916–1981), German rocket scientist *Helmut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square-free Integer
In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, is square-free, but is not, because 18 is divisible by . The smallest positive square-free numbers are Square-free factorization Every positive integer n can be factored in a unique way as n=\prod_^k q_i^i, where the q_i different from one are square-free integers that are pairwise coprime. This is called the ''square-free factorization'' of . To construct the square-free factorization, let n=\prod_^h p_j^ be the prime factorization of n, where the p_j are distinct prime numbers. Then the factors of the square-free factorization are defined as q_i=\prod_p_j. An integer is square-free if and only if q_i=1 for all i > 1. An integer greater than one is the kth power of another integer if and only if k is a divisor of all i such that q_i\neq 1. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Factor
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which alwa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
105 (number)
105 (one hundred ndfive) is the natural number following 104 and preceding 106. In mathematics 105 is a triangular number, a dodecagonal number, and the first Zeisel number. It is the first odd sphenic number and is the product of three consecutive prime numbers. 105 is the double factorial of 7. It is also the sum of the first five square pyramidal numbers. 105 comes in the middle of the prime quadruplet (101, 103, 107, 109). The only other such numbers less than a thousand are 9, 15, 195, and 825. 105 is also the middle of the only prime sextuplet (97, 101, 103, 107, 109, 113) between the ones occurring at 7-23 and at 16057–16073. As the product of the first three odd primes (3\times5\times7) and less than the square of the next prime (11) by > 8, for n=105, n ± 2, ± 4, and ± 8 must be prime, and n ± 6, ± 10, ± 12, and ± 14 must be composite (prime gap). 105 is also a pseudoprime to the prime bases 13, 29, 41, 43, 71, 83, and 97. The distinct prime factors of 10 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1729 (number)
1729 is the natural number following 1728 and preceding 1730. It is a taxicab number, and is variously known as Ramanujan's number and the Ramanujan-Hardy number, after an anecdote of the British mathematician G. H. Hardy when he visited Indian mathematician Srinivasa Ramanujan in hospital. He related their conversation: The two different ways are: : 1729 = 13 + 123 = 93 + 103 The quotation is sometimes expressed using the term "positive cubes", since allowing negative perfect cubes (the cube of a negative integer) gives the smallest solution as 91 (which is a divisor of 1729; 1991 = 1729). :91 = 63 + (−5)3 = 43 + 33 Numbers that are the smallest number that can be expressed as the sum of two cubes in ''n'' distinct ways have been dubbed " taxicab numbers". The number was also found in one of Ramanujan's notebooks dated years before the incident, and was noted by Frénicle de Bessy in 1657. A commemorative plaque now appears at the site of the Ramanujan-Hardy incid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carmichael Number
In number theory, a Carmichael number is a composite number n, which in modular arithmetic satisfies the congruence relation: :b^n\equiv b\pmod for all integers b. The relation may also be expressed in the form: :b^\equiv 1\pmod. for all integers b which are relatively prime to n. Carmichael numbers are named after American mathematician Robert Carmichael, the term having been introduced by Nicolaas Beeger in 1950 ( Øystein Ore had referred to them in 1948 as numbers with the "Fermat property", or "''F'' numbers" for short). They are infinite in number. They constitute the comparatively rare instances where the strict converse of Fermat's Little Theorem does not hold. This fact precludes the use of that theorem as an absolute test of primality. The Carmichael numbers form the subset ''K''1 of the Knödel numbers. Overview Fermat's little theorem states that if ''p'' is a prime number, then for any integer ''b'', the number ''b'' − ''b'' is an integer mul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which alw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
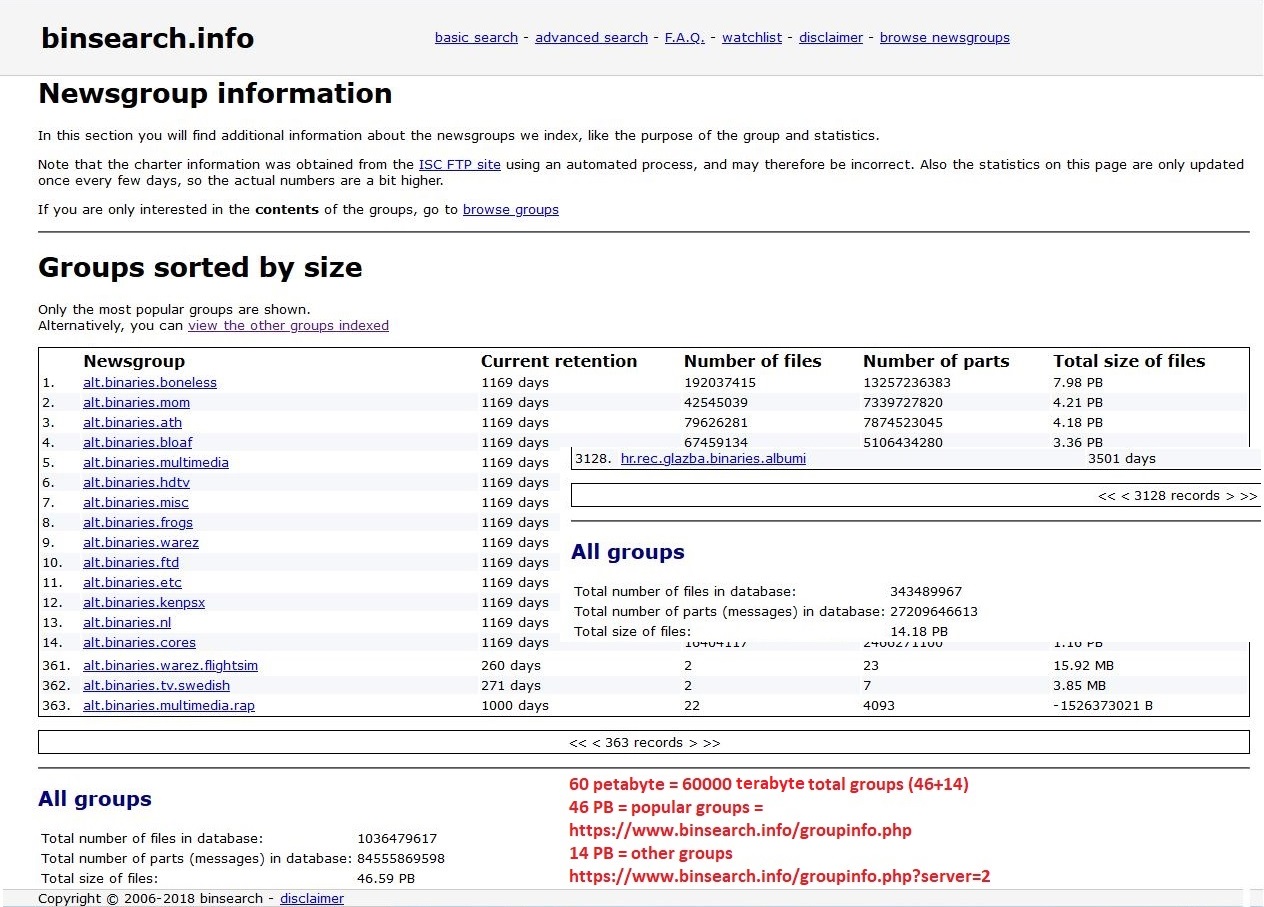
Newsgroup
A Usenet newsgroup is a repository usually within the Usenet system, for messages posted from users in different locations using the Internet. They are discussion groups and are not devoted to publishing news. Newsgroups are technically distinct from, but functionally similar to, discussion forums on the World Wide Web. Newsreader software is used to read the content of newsgroups. Before the adoption of the World Wide Web, Usenet newsgroups were among the most popular Internet services, and have retained their noncommercial nature in contrast to the increasingly ad-laden web. In recent years, this form of open discussion on the Internet has lost considerable ground to individually-operated browser-accessible forums and big media social networks such as Facebook and Twitter. Communication is facilitated by the Network News Transfer Protocol (NNTP) which allows connection to Usenet servers and data transfer over the internet. Similar to another early (yet still used) prot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |