|
Wyckoff Position
In crystallography, a Wyckoff position is any point in a set of points whose site symmetry groups (see below) are all conjugate subgroups one of another. Crystallography tables give the Wyckoff positions for different space groups. History The Wyckoff positions are named after Ralph Wyckoff, an American X-ray crystallographer who authored several books in the field. His 1922 book, The Analytical Expression of the Results of the Theory of Space Groups, contained tables with the positional coordinates, both general and special, permitted by the symmetry elements. This book was the forerunner of International Tables for X-ray Crystallography, which first appeared in 1935. Definition For any point in a unit cell, given by fractional coordinates, one can apply a symmetry operation to the point. In some cases it will move to new coordinates, while in other cases the point will remain unaffected. For example, reflecting across a mirror plane will switch all the points left and right o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In July 2012, the United Nations recognised the importance of the science of crystallography by proclaiming 2014 the International Year of Crystallography.UN announcement "International Year of Crystallography" iycr2014.org. 12 July 2012 Crystallography is a broad topic, and many of its subareas, such as X-ray crystallography, are themselves important scientific topics. Crystallography ranges from the fundamentals of crystal structure to the mathematics of Crystal system, crystal geometry, including those that are Aperiodic crystal, not periodic or quasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Groups
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups. In crystallography, space groups are also called the crystallographic or Fedorov groups, and represent a description of the symmetry of the crystal. A definitive source regarding 3-dimensional space groups is the ''International Tables for Crystallography'' . History Space groups in 2 dimensions are the 17 wallpaper groups which have been known for several centuries, though the proof that the list ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ralph Wyckoff
Ralph Walter Graystone Wyckoff, Sr. (August 9, 1897 – November 3, 1994), or simply Ralph Wyckoff, was an American chemist and pioneer of X-ray crystallography. He also made contributions to vaccine developments against epidemic typhus and other viruses. Biography Wyckoff was the son of judge Abram Ralph Wyckoff and Ethel Agnes Catchpole. He studied at Hobart College, where he obtained a Bachelor of Science in 1916. He continued his studies at Cornell University, where he obtained his Ph.D. in 1919. In 1916, he published his first scientific paper (of more than 400) at the age of nineteen in the ''Journal of the American Chemical Society''. Under Shoji Nishikawa, he presented his thesis about the crystallographic resolution of the structures of NaNO3 and CsICl2 in 1919. Wyckoff continued working in X-ray crystallography and wrote several books about the topic. Wyckoff's 1922 book, ''The Analytical Expression of the Results of the Theory of Space Groups'', contained tables wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
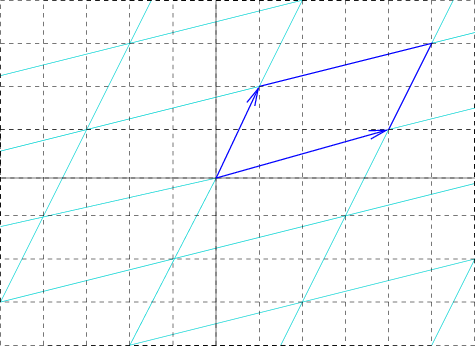
Unit Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ..., for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Coordinates
In crystallography, a fractional coordinate system (crystal coordinate system) is a coordinate system in which basis vectors used to describe the space are the lattice vectors of a crystal (periodic) pattern. The selection of an origin and a basis define a unit cell, a parallelotope (i.e., generalization of a parallelogram (2D) or parallelepiped (3D) in higher dimensions) defined by the lattice basis vectors \mathbf _1, \mathbf _2, \dots, \mathbf _d where d is the dimension of the space. These basis vectors are described by lattice parameters (lattice constants) consisting of the lengths of the lattice basis vectors a_1, a_2, \dots, a_d and the angles between them \alpha_1, \alpha_2, \dots, \alpha_. Most cases in crystallography involve two- or three-dimensional space. In the three-dimensional case, the basis vectors \mathbf _1, \mathbf _2, \mathbf _3 are commonly displayed as \mathbf, \mathbf, \mathbf with their lengths denoted by a, b, c respectively, and the angles deno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry Operation
In mathematics, a symmetry operation is a geometric transformation of an object that leaves the object looking the same after it has been carried out. For example, a turn rotation of a regular triangle about its center (geometry), center, a reflection (mathematics), reflection of a square across its diagonal, a translation (geometry), translation of the Euclidean plane, or a point reflection of a sphere through its center are all symmetry operations. Each symmetry operation is performed with respect to some symmetry element (a point, line or plane). In the context of molecular symmetry, a symmetry operation is a permutation of atoms such that the molecule or crystal is transformed into a state indistinguishable from the starting state. Two basic facts follow from this definition, which emphasizes its usefulness. # Physical properties must be Invariant (physics), invariant with respect to symmetry operations. # Symmetry operations can be collected together in groups which are isomo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Group
In geometry, a point group is a group (mathematics), mathematical group of symmetry operations (isometry, isometries in a Euclidean space) that have a Fixed point (mathematics), fixed point in common. The Origin (mathematics), coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every point group in dimension ''d'' is then a subgroup of the orthogonal group O(''d''). Point groups are used to describe the Symmetry (geometry), symmetries of geometric figures and physical objects such as molecular symmetry, molecules. Each point group can be Group representation, represented as sets of orthogonal matrix, orthogonal matrices ''M'' that transform point ''x'' into point ''y'' according to . Each element of a point group is either a Rotation (mathematics), rotation (determinant of ), or it is a Reflection (mathematics), reflection or improper rotation (determinant of ). The geometric symmetries of crystals are described by space groups, which allow T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugacy Class
In mathematics, especially group theory, two elements a and b of a group are conjugate if there is an element g in the group such that b = gag^. This is an equivalence relation whose equivalence classes are called conjugacy classes. In other words, each conjugacy class is closed under b = gag^ for all elements g in the group. Members of the same conjugacy class cannot be distinguished by using only the group structure, and therefore share many properties. The study of conjugacy classes of non-abelian groups is fundamental for the study of their structure. For an abelian group, each conjugacy class is a set containing one element ( singleton set). Functions that are constant for members of the same conjugacy class are called class functions. Definition Let G be a group. Two elements a, b \in G are conjugate if there exists an element g \in G such that gag^ = b, in which case b is called of a and a is called a conjugate of b. In the case of the general linear group \op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inversion Point
In geometry, a point reflection (also called a point inversion or central inversion) is a geometric transformation of affine space in which every point is reflected across a designated inversion center, which remains fixed. In Euclidean or pseudo-Euclidean spaces, a point reflection is an isometry (preserves distance). In the Euclidean plane, a point reflection is the same as a half-turn rotation (180° or radians), while in three-dimensional Euclidean space a point reflection is an improper rotation which preserves distances but reverses orientation. A point reflection is an involution: applying it twice is the identity transformation. An object that is invariant under a point reflection is said to possess point symmetry (also called inversion symmetry or central symmetry). A point group including a point reflection among its symmetries is called ''centrosymmetric''. Inversion symmetry is found in many crystal structures and molecules, and has a major effect upon their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Improper Rotation
In geometry, an improper rotation. (also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion) is an isometry in Euclidean space that is a combination of a Rotation (geometry), rotation about an axis and a reflection (mathematics), reflection in a plane perpendicular to that axis. Reflection and Point reflection, inversion are each a special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation.. It is used as a symmetry operation in the context of Symmetry (geometry), geometric symmetry, molecular symmetry and Crystallographic point group, crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have ''improper rotation symmetry''. Three dimensions In 3 dimensions, improper rotation is equivalently defined as a combination of rotation about an axis and inversion in a point on the axis. For this reason ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Screw Axes
A screw axis (helical axis or twist axis) is a line that is simultaneously the axis of rotation and the line along which translation of a body occurs. Chasles' theorem shows that each Euclidean displacement in three-dimensional space has a screw axis, and the displacement can be decomposed into a rotation about and a slide along this screw axis. Plücker coordinates are used to locate a screw axis in space, and consist of a pair of three-dimensional vectors. The first vector identifies the direction of the axis, and the second locates its position. The special case when the first vector is zero is interpreted as a pure translation in the direction of the second vector. A screw axis is associated with each pair of vectors in the algebra of screws, also known as screw theory. The spatial movement of a body can be represented by a continuous set of displacements. Because each of these displacements has a screw axis, the movement has an associated ruled surface known as a ''screw s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glide Plane
In geometry, a glide reflection or transflection is a geometric transformation that consists of a reflection across a hyperplane and a translation ("glide") in a direction parallel to that hyperplane, combined into a single transformation. Because the distances between points are not changed under glide reflection, it is a motion or isometry. When the context is the two-dimensional Euclidean plane, the hyperplane of reflection is a straight line called the ''glide line'' or ''glide axis''. When the context is three-dimensional space, the hyperplane of reflection is a plane called the ''glide plane''. The displacement vector of the translation is called the ''glide vector''. When some geometrical object or configuration appears unchanged by a transformation, it is said to have symmetry, and the transformation is called a symmetry operation. ''Glide-reflection symmetry'' is seen in frieze groups (patterns which repeat in one dimension, often used in decorative borders), wallpaper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |