|
Woodbury Matrix Identity
In mathematics, specifically linear algebra, the Woodbury matrix identity – named after Max A. Woodbury – says that the inverse of a rank-''k'' correction of some matrix can be computed by doing a rank-''k'' correction to the inverse of the original matrix. Alternative names for this formula are the matrix inversion lemma, Sherman–Morrison–Woodbury formula or just Woodbury formula. However, the identity appeared in several papers before the Woodbury report. The Woodbury matrix identity is \left(A + UCV \right)^ = A^ - A^U \left(C^ + VA^U \right)^ VA^, where ''A'', ''U'', ''C'' and ''V'' are conformable matrices: ''A'' is ''n''×''n'', ''C'' is ''k''×''k'', ''U'' is ''n''×''k'', and ''V'' is ''k''×''n''. This can be derived using blockwise matrix inversion. While the identity is primarily used on matrices, it holds in a general ring or in an Ab-category. The Woodbury matrix identity allows cheap computation of inverses and solutions to linear equations. However ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schur Complement
The Schur complement is a key tool in the fields of linear algebra, the theory of matrices, numerical analysis, and statistics. It is defined for a block matrix. Suppose ''p'', ''q'' are nonnegative integers such that ''p + q > 0'', and suppose ''A'', ''B'', ''C'', ''D'' are respectively ''p'' × ''p'', ''p'' × ''q'', ''q'' × ''p'', and ''q'' × ''q'' matrices of complex numbers. Let M = \begin A & B \\ C & D \end so that ''M'' is a (''p'' + ''q'') × (''p'' + ''q'') matrix. If ''D'' is invertible, then the Schur complement of the block ''D'' of the matrix ''M'' is the ''p'' × ''p'' matrix defined by M/D := A - BD^C. If ''A'' is invertible, the Schur complement of the block ''A'' of the matrix ''M'' is the ''q'' × ''q'' matrix defined by M/A := D - CA^B. In the case that ''A'' or ''D'' is singular, substituting a generalized inverse for the inverses on ''M/A'' and ''M/D'' yields the generalized Schur complement. The Schur complement is named after Issai Schur who used it to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moore–Penrose Inverse
In mathematics, and in particular linear algebra, the Moore–Penrose inverse of a matrix , often called the pseudoinverse, is the most widely known generalization of the inverse matrix. It was independently described by E. H. Moore in 1920, Arne Bjerhammar in 1951, and Roger Penrose in 1955. Earlier, Erik Ivar Fredholm had introduced the concept of a pseudoinverse of integral operators in 1903. The terms ''pseudoinverse'' and ''generalized inverse'' are sometimes used as synonyms for the Moore–Penrose inverse of a matrix, but sometimes applied to other elements of algebraic structures which share some but not all properties expected for an inverse element. A common use of the pseudoinverse is to compute a "best fit" ( least squares) approximate solution to a system of linear equations that lacks an exact solution (see below under § Applications). Another use is to find the minimum ( Euclidean) norm solution to a system of linear equations with multiple solutions. The pseu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemmas In Linear Algebra , part of a neuron
{{Disambiguation ...
Lemma (from Ancient Greek ''premise'', ''assumption'', from Greek ''I take'', ''I get'') may refer to: Language and linguistics * Lemma (morphology), the canonical, dictionary or citation form of a word * Lemma (psycholinguistics), a mental abstraction of a word about to be uttered Science and mathematics * Lemma (botany), a part of a grass plant * Lemma (mathematics), a proven proposition used as a step in a larger proof Other uses * ''Lemma'' (album), by John Zorn (2013) See also *Analemma, a diagram showing the variation of the position of the Sun in the sky *Dilemma * Lema (other) * Lemmatisation *Neurolemma Neurilemma (also known as neurolemma, sheath of Schwann, or Schwann's sheath) is the outermost cell nucleus, nucleated cytoplasmic layer of Schwann cells (also called neurilemmocytes) that surrounds the axon of the neuron. It forms the outermost la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invertible Matrix
In linear algebra, an invertible matrix (''non-singular'', ''non-degenarate'' or ''regular'') is a square matrix that has an inverse. In other words, if some other matrix is multiplied by the invertible matrix, the result can be multiplied by an inverse to undo the operation. An invertible matrix multiplied by its inverse yields the identity matrix. Invertible matrices are the same size as their inverse. Definition An -by- square matrix is called invertible if there exists an -by- square matrix such that\mathbf = \mathbf = \mathbf_n ,where denotes the -by- identity matrix and the multiplication used is ordinary matrix multiplication. If this is the case, then the matrix is uniquely determined by , and is called the (multiplicative) ''inverse'' of , denoted by . Matrix inversion is the process of finding the matrix which when multiplied by the original matrix gives the identity matrix. Over a field, a square matrix that is ''not'' invertible is called singular or deg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the matrix and the linear map represented, on a given basis (linear algebra), basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible matrix, invertible and the corresponding linear map is an linear isomorphism, isomorphism. However, if the determinant is zero, the matrix is referred to as singular, meaning it does not have an inverse. The determinant is completely determined by the two following properties: the determinant of a product of matrices is the product of their determinants, and the determinant of a triangular matrix is the product of its diagonal entries. The determinant of a matrix is :\begin a & b\\c & d \end=ad-bc, and the determinant of a matrix is : \begin a & b & c \\ d & e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Determinant Lemma
In mathematics, in particular linear algebra, the matrix determinant lemma computes the determinant of the sum of an invertible matrix A and the dyadic product, uvT, of a column vector u and a row vector vT. Statement Suppose A is an invertible square matrix and u, v are column vectors. Then the matrix determinant lemma states that :\det(\mathbf + \mathbf^\textsf) = (1 + \mathbf^\textsf\mathbf^\mathbf)\,\det(\mathbf)\,. Here, uvT is the outer product of two vectors u and v. The theorem can also be stated in terms of the adjugate matrix of A: :\det(\mathbf + \mathbf^\textsf) = \det(\mathbf) + \mathbf^\textsf\mathrm(\mathbf)\mathbf\,, in which case it applies whether or not the matrix A is invertible. Proof First the proof of the special case A = I follows from the equality: : \begin \mathbf & 0 \\ \mathbf^\textsf & 1 \end \begin \mathbf + \mathbf^\textsf & \mathbf \\ 0 & 1 \end \begin \mathbf & 0 \\ -\mathbf^\textsf & 1 \end = \begin \mathbf & \mathbf \\ 0 & 1 + \m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Partial Differential Equations
{{disambig ...
Numerical may refer to: * Number * Numerical digit * Numerical analysis Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Linear Algebra
Numerical linear algebra, sometimes called applied linear algebra, is the study of how matrix operations can be used to create computer algorithms which efficiently and accurately provide approximate answers to questions in continuous mathematics. It is a subfield of numerical analysis, and a type of linear algebra. Computers use floating-point arithmetic and cannot exactly represent irrational data, so when a computer algorithm is applied to a matrix of data, it can sometimes increase the difference between a number stored in the computer and the true number that it is an approximation of. Numerical linear algebra uses properties of vectors and matrices to develop computer algorithms that minimize the error introduced by the computer, and is also concerned with ensuring that the algorithm is as efficient as possible. Numerical linear algebra aims to solve problems of continuous mathematics using finite precision computers, so its applications to the natural and social scienc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Solution
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point, as functions of one or several variables called parameters. In the case of a single parameter, parametric equations are commonly used to express the trajectory of a moving point, in which case, the parameter is often, but not necessarily, time, and the point describes a curve, called a parametric curve. In the case of two parameters, the point describes a surface, called a parametric surface. In all cases, the equations are collectively called a parametric representation, or parametric system, or parameterization (also spelled parametrization, parametrisation) of the object. For example, the equations \begin x &= \cos t \\ y &= \sin t \end form a parametric representation of the unit circle, where is the parameter: A point is on the unit circle if and only if there is a value of such that these two equations generate that point. Sometimes the parametric equations f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
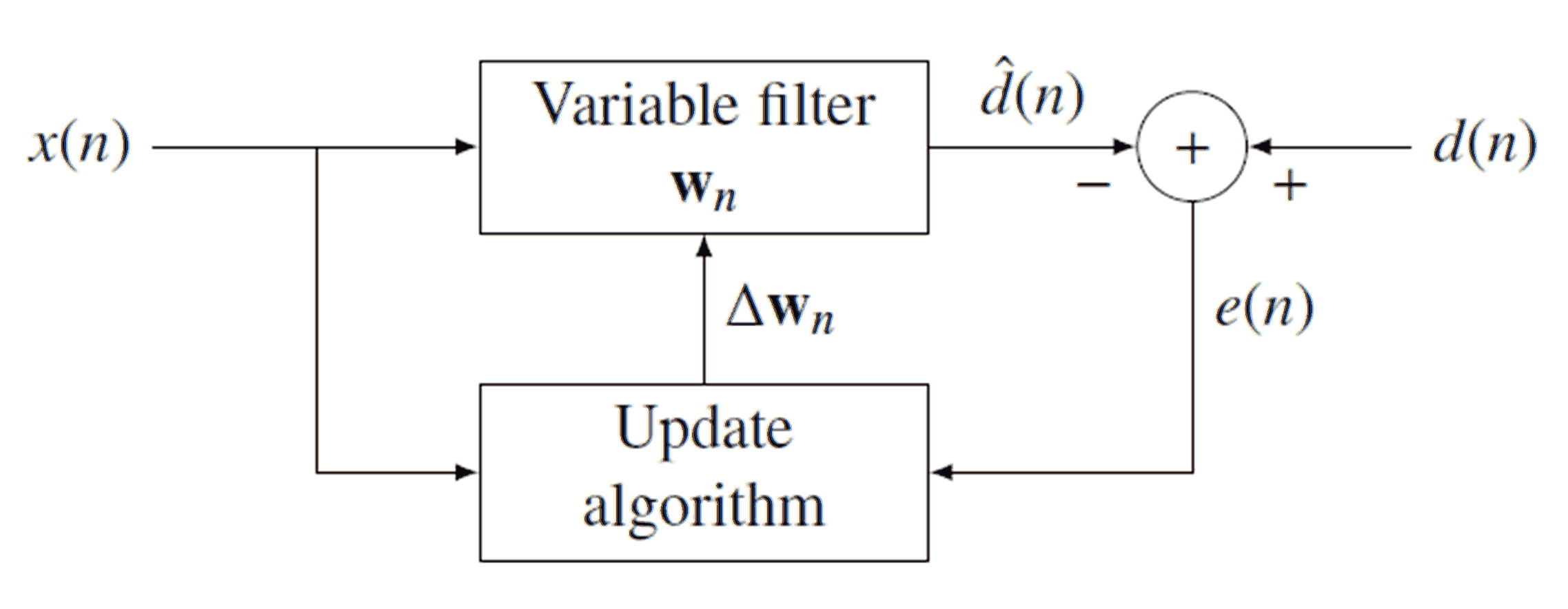
Recursive Least Squares
Recursive least squares (RLS) is an adaptive filter algorithm that recursively finds the coefficients that minimize a Weighted least squares, weighted linear least squares Loss function, cost function relating to the input signals. This approach is in contrast to other algorithms such as the least mean squares (LMS) that aim to reduce the mean square error. In the derivation of the RLS, the input signals are considered deterministic system (mathematics), deterministic, while for the LMS and similar algorithms they are considered stochastic. Compared to most of its competitors, the RLS exhibits extremely fast convergence. However, this benefit comes at the cost of high computational complexity. Motivation RLS was discovered by Carl Friedrich Gauss, Gauss but lay unused or ignored until 1950 when Plackett rediscovered the original work of Gauss from 1821. In general, the RLS can be used to solve any problem that can be solved by adaptive filters. For example, suppose that a signal d( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kalman Filter
In statistics and control theory, Kalman filtering (also known as linear quadratic estimation) is an algorithm that uses a series of measurements observed over time, including statistical noise and other inaccuracies, to produce estimates of unknown variables that tend to be more accurate than those based on a single measurement, by estimating a joint probability distribution over the variables for each time-step. The filter is constructed as a mean squared error minimiser, but an alternative derivation of the filter is also provided showing how the filter relates to maximum likelihood statistics. The filter is named after Rudolf E. Kálmán. Kalman filtering has numerous technological applications. A common application is for guidance, navigation, and control of vehicles, particularly aircraft, spacecraft and ships Dynamic positioning, positioned dynamically. Furthermore, Kalman filtering is much applied in time series analysis tasks such as signal processing and econometrics. K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |