|
Winkel Projection
The Winkel projection is a group of three map projections proposed in 1921 by the German cartographer Oswald Winkel (7 January 1874 – 18 July 1953). Winkel projections use the arithmetic mean of the equirectangular projection and other projections. There are several variants: the Winkel I projection uses the sinusoidal projection, Winkel II uses the Mollweide projection, and Winkel Tripel (Winkel III) uses the Aitoff projection. Winkel I and II are pseudocylindrical projections, while Winkel III is an azimuthal projection. Of these three variants, the Winkel tripel projection is the most widely known. See also * List of map projections This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise WP:NOTABLE, notable. Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of proj ... References {{Map projections Map projections ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, proje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
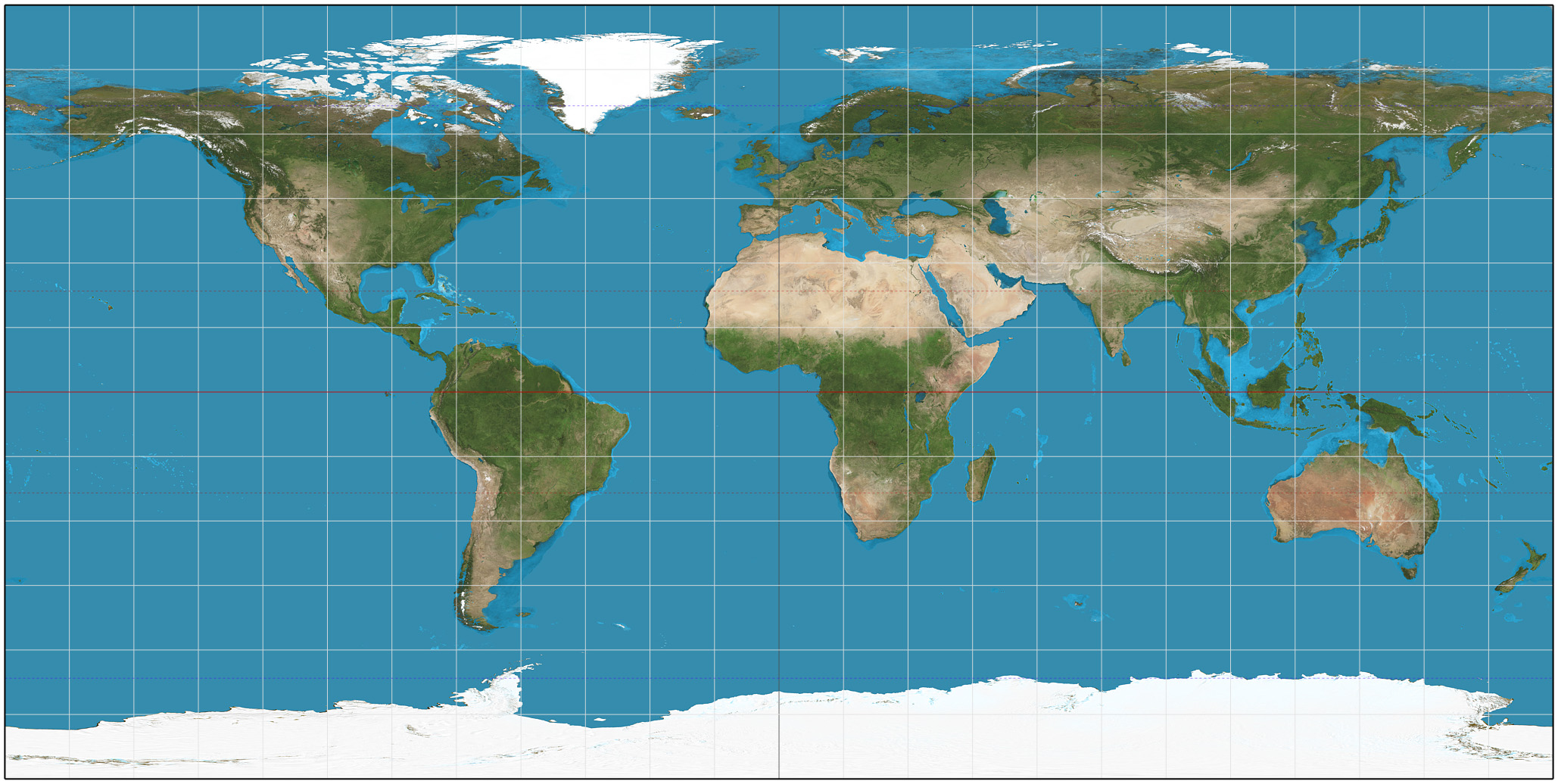
Equirectangular Projection
The equirectangular projection (also called the equidistant cylindrical projection or la carte parallélogrammatique projection), and which includes the special case of the plate carrée projection (also called the geographic projection, lat/lon projection, or plane chart), is a simple map projection attributed to Marinus of Tyre who, Ptolemy claims, invented the projection about AD 100. The projection maps meridian (geography), meridians to vertical straight lines of constant spacing (for meridional intervals of constant spacing), and circle of latitude, circles of latitude to horizontal straight lines of constant spacing (for constant intervals of circle of latitude, parallels). The projection is neither equal-area projection, equal area nor conformal map projection, conformal. Because of the distortions introduced by this projection, it has little use in navigation or cadastral mapping and finds its main use in thematic mapping. In particular, the plate carrée has become a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinusoidal Projection
The sinusoidal projection is a pseudocylindrical equal-area map projection, sometimes called the Sanson–Flamsteed or the Mercator equal-area projection. Jean Cossin of Dieppe was one of the first mapmakers to use the sinusoidal, using it in a world map in 1570. The projection represents the poles as points, as they are on the sphere, but the meridians and continents are distorted. The equator and the central meridian are the most accurate parts of the map, having no distortion at all, and the further away from those that one examines, the greater the distortion. The projection is defined by: :\begin x &= \left(\lambda - \lambda_0\right) \cos \varphi \\ y &= \varphi\,\end where \varphi is the latitude, ''λ'' is the longitude, and ''λ'' is the longitude of the central meridian. Scale is constant along the central meridian, and east–west scale is constant throughout the map. Therefore, the length of each parallel on the map is proportional to the cosine of the latitude, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mollweide Projection
400px, Mollweide projection of the world 400px, The Mollweide projection with Tissot's indicatrix of deformation The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions. The projection was first published by mathematician and astronomer Karl (or Carl) Brandan Mollweide (1774–1825) of Leipzig in 1805. It was reinvented and popularized in 1857 by Jacques Babinet, who gave it the name homalographic projection. The variation homolographic arose from frequent nineteenth-century usage in star atlases. Properties The Mollweide is a pseudocylindrical projection in which the equator is represented as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Winkel Tripel Projection
The Winkel tripel projection (Winkel III), a modified azimuthal map projection of the world map, world, is one of Winkel projection, three projections proposed by German cartographer Oswald Winkel (7 January 1874 – 18 July 1953) in 1921. The projection is the arithmetic mean of the equirectangular projection and the Aitoff projection: The name (German language, German for 'triple') refers to Winkel's goal of minimizing three Map projection#Metric properties of maps, kinds of distortion: area, direction, and distance. Algorithm : \begin x &= \frac \left(\lambda \cos \varphi_1 + \frac\right), \\ y &= \frac \left(\varphi + \frac\right), \end where ''λ'' is the longitude relative to the central meridian of the projection, ''φ'' is the latitude, ''φ'' is the standard parallel for the equirectangular projection, sinc is the sinc function, unnormalized cardinal sine function, and : \alpha = \arccos\left(\cos\varphi \cos \frac \right). In his proposal, Winkel set : \varphi_1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aitoff Projection
The Aitoff projection is a modified azimuthal map projection proposed by David A. Aitoff in 1889. Based on the equatorial form of the azimuthal equidistant projection, Aitoff first halves longitudes, then projects according to the azimuthal equidistant, and then stretches the result horizontally into a 2:1 ellipse to compensate for having halved the longitudes. Expressed simply: :x = 2 \operatorname_x\left(\frac, \varphi\right), \qquad y = \operatorname_y \left(\frac\lambda 2, \varphi \right) where azeq and azeq are the ''x'' and ''y'' components of the equatorial azimuthal equidistant projection. Written out explicitly, the projection is: :x = \frac, \qquad y = \frac where :\alpha = \arccos\left(\cos\varphi\cos\frac\right)\, and sinc ''α'' is the unnormalized sinc function with the discontinuity removed. In all of these formulas, ''λ'' is the longitude from the central meridian and ''φ'' is the latitude. Three years later, Ernst Hermann Heinrich Hammer suggested ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise WP:NOTABLE, notable. Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection surface ; Cylindrical: In normal aspect, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In normal aspect, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In normal aspect, conic (or conical) projections map meridians as straight lines, and parallels as arcs of circles. ; Pseudoconical: In normal aspect, pseudoconical projections represent the central meridian as a straight line, other meridians as complex curves, and parallels as ci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |