|
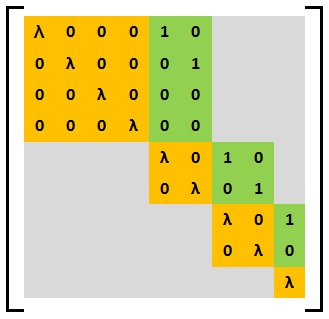
Weyr Canonical Form
In mathematics, in linear algebra, a Weyr canonical form (or, Weyr form or Weyr matrix) is a square matrix which (in some sense) induces "nice" properties with matrices it commutes with. It also has a particularly simple structure and the conditions for possessing a Weyr form are fairly weak, making it a suitable tool for studying classes of commuting matrices. A square matrix is said to be ''in'' the Weyr canonical form if the matrix has the structure defining the Weyr canonical form. The Weyr form was discovered by the Czech Republic, Czech mathematician Eduard Weyr in 1885. The Weyr form did not become popular among mathematicians and it was overshadowed by the closely related, but distinct, canonical form known by the name Jordan normal form, Jordan canonical form. The Weyr form has been rediscovered several times since Weyr’s original discovery in 1885. This form has been variously called as ''modified Jordan form,'' ''reordered Jordan form,'' ''second Jordan form,'' and ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Matrix
In linear algebra, a diagonal matrix is a matrix (mathematics), matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices. Elements of the main diagonal can either be zero or nonzero. An example of a 2×2 diagonal matrix is \left[\begin 3 & 0 \\ 0 & 2 \end\right], while an example of a 3×3 diagonal matrix is \left[\begin 6 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 4 \end\right]. An identity matrix of any size, or any multiple of it is a diagonal matrix called a #Scalar matrix, ''scalar matrix'', for example, \left[\begin 0.5 & 0 \\ 0 & 0.5 \end\right]. In geometry, a diagonal matrix may be used as a ''scaling matrix'', since matrix multiplication with it results in changing scale (size) and possibly also shape; only a scalar matrix results in uniform change in scale. Definition As stated above, a diagonal matrix is a matrix in which all off-diagonal entries are zero. That is, the matrix with columns and rows is diagonal if \forall i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenspace
In linear algebra, an eigenvector ( ) or characteristic vector is a Vector (mathematics and physics), vector that has its direction (geometry), direction unchanged (or reversed) by a given linear map, linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scalar multiplication, scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative number, negative or complex number, complex number). Euclidean vector, Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation Rotation (mathematics), rotates, Scaling (geometry), stretches, or Shear mapping, shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with nei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nilpotent Matrix
In linear algebra, a nilpotent matrix is a square matrix ''N'' such that :N^k = 0\, for some positive integer k. The smallest such k is called the index of N, sometimes the degree of N. More generally, a nilpotent transformation is a linear transformation L of a vector space such that L^k = 0 for some positive integer k (and thus, L^j = 0 for all j \geq k). Both of these concepts are special cases of a more general concept of nilpotent, nilpotence that applies to elements of ring (algebra), rings. Examples Example 1 The matrix : A = \begin 0 & 1 \\ 0 & 0 \end is nilpotent with index 2, since A^2 = 0. Example 2 More generally, any n-dimensional triangular matrix with zeros along the main diagonal is nilpotent, with index \le n . For example, the matrix : B=\begin 0 & 2 & 1 & 6\\ 0 & 0 & 1 & 2\\ 0 & 0 & 0 & 3\\ 0 & 0 & 0 & 0 \end is nilpotent, with : B^2=\begin 0 & 0 & 2 & 7\\ 0 & 0 & 0 & 3\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end ;\ B^3=\begin 0 & 0 & 0 & 6\\ 0 & 0 & 0 & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diagonal Matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices. Elements of the main diagonal can either be zero or nonzero. An example of a 2×2 diagonal matrix is \left begin 3 & 0 \\ 0 & 2 \end\right/math>, while an example of a 3×3 diagonal matrix is \left begin 6 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 4 \end\right/math>. An identity matrix of any size, or any multiple of it is a diagonal matrix called a ''scalar matrix'', for example, \left begin 0.5 & 0 \\ 0 & 0.5 \end\right/math>. In geometry, a diagonal matrix may be used as a '' scaling matrix'', since matrix multiplication with it results in changing scale (size) and possibly also shape; only a scalar matrix results in uniform change in scale. Definition As stated above, a diagonal matrix is a matrix in which all off-diagonal entries are zero. That is, the matrix with columns and rows is diagonal if \forall i,j \in \, i \ne j \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Similarity
In linear algebra, two ''n''-by-''n'' matrices and are called similar if there exists an invertible ''n''-by-''n'' matrix such that B = P^ A P . Similar matrices represent the same linear map under two possibly different bases, with being the change-of-basis matrix. A transformation is called a similarity transformation or conjugation of the matrix . In the general linear group, similarity is therefore the same as conjugacy, and similar matrices are also called conjugate; however, in a given subgroup of the general linear group, the notion of conjugacy may be more restrictive than similarity, since it requires that be chosen to lie in . Motivating example When defining a linear transformation, it can be the case that a change of basis can result in a simpler form of the same transformation. For example, the matrix representing a rotation in when the axis of rotation is not aligned with the coordinate axis can be complicated to compute. If the axis of rotation were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jordan–Chevalley Decomposition
In mathematics, specifically linear algebra, the Jordan–Chevalley decomposition, named after Camille Jordan and Claude Chevalley, expresses a linear operator in a unique way as the sum of two other linear operators which are simpler to understand. Specifically, one part is potentially diagonalisable and the other is nilpotent. The two parts are polynomials in the operator, which makes them behave nicely in algebraic manipulations. The decomposition has a short description when the Jordan normal form of the operator is given, but it exists under weaker hypotheses than are needed for the existence of a Jordan normal form. Hence the Jordan–Chevalley decomposition can be seen as a generalisation of the Jordan normal form, which is also reflected in several proofs of it. It is closely related to the Wedderburn principal theorem about associative algebras, which also leads to several analogues in Lie algebras. Analogues of the Jordan–Chevalley decomposition also exist for elements ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraically Closed Field
In mathematics, a field is algebraically closed if every non-constant polynomial in (the univariate polynomial ring with coefficients in ) has a root in . In other words, a field is algebraically closed if the fundamental theorem of algebra holds for it. Every field K is contained in an algebraically closed field C, and the roots in C of the polynomials with coefficients in K form an algebraically closed field called an algebraic closure of K. Given two algebraic closures of K there are isomorphisms between them that fix the elements of K. Algebraically closed fields appear in the following chain of class inclusions: Examples As an example, the field of real numbers is not algebraically closed, because the polynomial equation x^2+1=0 has no solution in real numbers, even though all its coefficients (1 and 0) are real. The same argument proves that no subfield of the real field is algebraically closed; in particular, the field of rational numbers is not algebraically cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basic Block
In compiler construction, a basic block is a straight-line code sequence with no branches in except to the entry and no branches out except at the exit. This restricted form makes a basic block highly amenable to analysis. Compilers usually decompose programs into their basic blocks as a first step in the analysis process. Basic blocks form the vertices or nodes in a control-flow graph. Definition The code in a basic block has: * One entry point, meaning that no code within it is the destination of a jump instruction anywhere in the program. * One exit point, meaning that only the last instruction can cause the program to begin executing code in a different basic block. Under these circumstances, whenever the first instruction in a basic block is executed, the rest of the instructions are necessarily executed exactly once and in order. The code may be source code, assembly code, or some other sequence of instructions. More formally, a sequence of instructions forms a basic b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere. It has unique properties, for example when the identity matrix represents a geometric transformation, the object remains unchanged by the transformation. In other contexts, it is analogous to multiplying by the number 1. Terminology and notation The identity matrix is often denoted by I_n, or simply by I if the size is immaterial or can be trivially determined by the context. I_1 = \begin 1 \end ,\ I_2 = \begin 1 & 0 \\ 0 & 1 \end ,\ I_3 = \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end ,\ \dots ,\ I_n = \begin 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end. The term unit matrix has also been widely used, but the term ''identity matrix'' is now standard. The term ''unit matrix'' is ambiguous, because it is also used for a matrix of on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |