|
Velocity Potential
A velocity potential is a scalar potential used in potential flow theory. It was introduced by Joseph-Louis Lagrange in 1788. It is used in continuum mechanics, when a continuum occupies a simply-connected region and is irrotational. In such a case, \nabla \times \mathbf =0 \,, where denotes the flow velocity. As a result, can be represented as the gradient of a scalar function : \mathbf = \nabla \varphi\ = \frac \mathbf + \frac \mathbf + \frac \mathbf \,. is known as a velocity potential for . A velocity potential is not unique. If is a velocity potential, then is also a velocity potential for , where is a scalar function of time and can be constant. Velocity potentials are unique up to a constant, or a function solely of the temporal variable. The Laplacian of a velocity potential is equal to the divergence of the corresponding flow. Hence if a velocity potential satisfies Laplace equation, the flow is incompressible. Unlike a stream function, a velocity potential ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Potential
In mathematical physics, scalar potential describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value ( scalar) that depends only on its location. A familiar example is potential energy due to gravity. A ''scalar potential'' is a fundamental concept in vector analysis and physics (the adjective ''scalar'' is frequently omitted if there is no danger of confusion with '' vector potential''). The scalar potential is an example of a scalar field. Given a vector field , the scalar potential is defined such that: \mathbf = -\nabla P = - \left( \frac, \frac, \frac \right), where is the gradient of and the second part of the equation is minus the gradient for a function of the Cartesian coordinates . In some cases, mathematicians may use a positive sign ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics technology may be called an Acoustical engineering, acoustical engineer. The application of acoustics is present in almost all aspects of modern society with the most obvious being the audio and noise control industries. Hearing (sense), Hearing is one of the most crucial means of survival in the animal world and speech is one of the most distinctive characteristics of human development and culture. Accordingly, the science of acoustics spreads across many facets of human society—music, medicine, architecture, industrial production, warfare and more. Likewise, animal species such as songbirds and frogs use sound and hearing as a key element of mating rituals or for marking territories. Art, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum Mechanics
Continuum mechanics is a branch of mechanics that deals with the deformation of and transmission of forces through materials modeled as a ''continuous medium'' (also called a ''continuum'') rather than as discrete particles. Continuum mechanics deals with ''deformable bodies'', as opposed to rigid bodies. A continuum model assumes that the substance of the object completely fills the space it occupies. While ignoring the fact that matter is made of atoms, this provides a sufficiently accurate description of matter on length scales much greater than that of inter-atomic distances. The concept of a continuous medium allows for intuitive analysis of bulk matter by using differential equations that describe the behavior of such matter according to physical laws, such as mass conservation, momentum conservation, and energy conservation. Information about the specific material is expressed in constitutive relationships. Continuum mechanics treats the physical properties of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
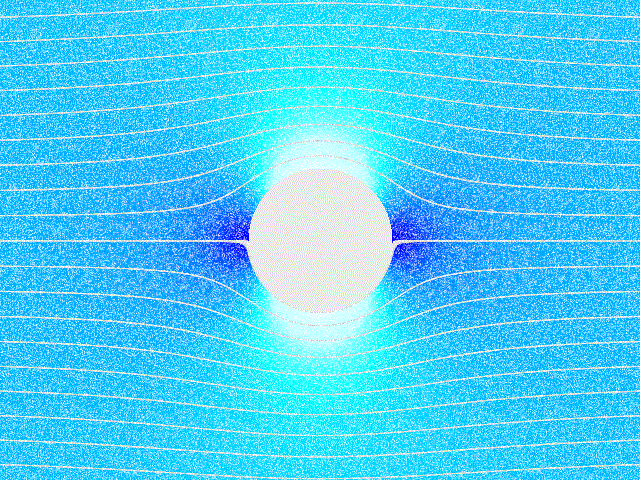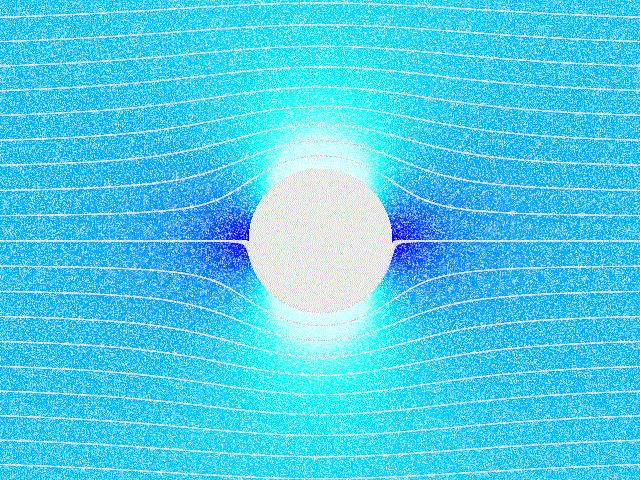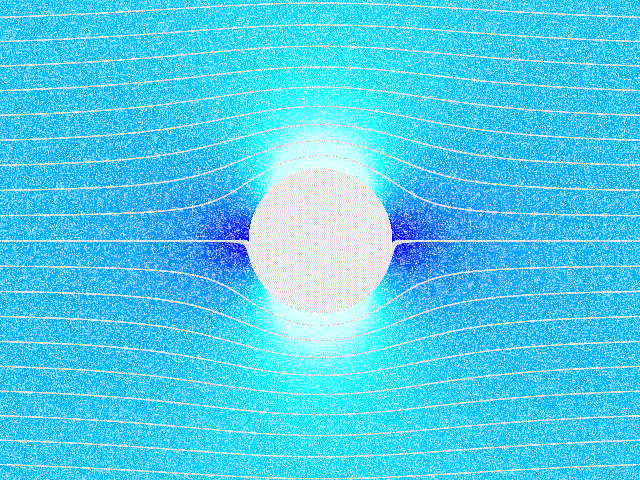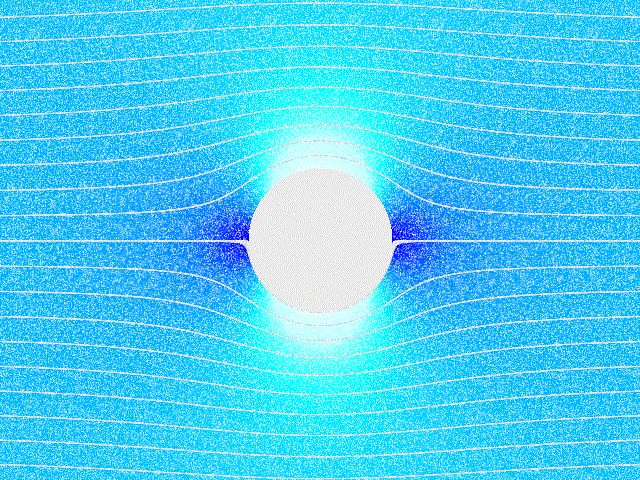
Potential Flow Around A Circular Cylinder
In mathematics, potential flow around a circular cylinder is a classical solution for the flow of an inviscid, incompressible fluid around a cylinder that is transverse to the flow. Far from the cylinder, the flow is unidirectional and uniform. The flow has no vorticity and thus the velocity field is irrotational and can be modeled as a potential flow. Unlike a real fluid, this solution indicates a net zero drag on the body, a result known as d'Alembert's paradox. Mathematical solution A cylinder (or disk) of radius is placed in a two-dimensional, incompressible, inviscid flow. The goal is to find the steady velocity vector and pressure in a plane, subject to the condition that far from the cylinder the velocity vector (relative to unit vectors and ) is: :\mathbf=U\mathbf+0\mathbf \,, where is a constant, and at the boundary of the cylinder :\mathbf\cdot\mathbf=0 \,, where is the vector normal to the cylinder surface. The upstream flow is uniform and has no vortic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Flow
In fluid dynamics, potential flow or irrotational flow refers to a description of a fluid flow with no vorticity in it. Such a description typically arises in the limit of vanishing viscosity, i.e., for an inviscid fluid and with no vorticity present in the flow. Potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an Conservative vector field#Irrotational vector fields, irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the Curl (mathematics), curl of the gradient of a Scalar (physics), scalar always being equal to zero. In the case of an incompressible flow the velocity potential satisfies Laplace's equation, and potential theory is applicable. However, potential flows also have been used to describe compressible flows and Hele-Shaw flows. The potential flow approach occurs in the modeling of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Fluid Mechanics
Hamiltonian fluid mechanics is the application of Hamiltonian mechanics, Hamiltonian methods to fluid mechanics. Note that this formalism only applies to non-dissipative fluids. Irrotational barotropic flow Take the simple example of a barotropic, inviscid vorticity-free fluid. Then, the Conjugate variables, conjugate fields are the mass density field ''ρ'' and the velocity potential ''φ''. The Poisson bracket is given by :\=\delta^d(\vec-\vec) and the Hamiltonian by: :H=\int \mathrm^d x \mathcal=\int \mathrm^d x \left( \frac\rho(\nabla \varphi)^2 +e(\rho) \right), where ''e'' is the internal energy density, as a function of ''ρ''. For this barotropic flow, the internal energy is related to the pressure ''p'' by: :e'' = \fracp', where an apostrophe ('), denotes differentiation with respect to ''ρ''. This Hamiltonian structure gives rise to the following two equations of motion: : \begin \frac&=+\frac= -\nabla \cdot(\rho\vec), \\ \frac&=-\frac=-\frac\ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vorticity
In continuum mechanics, vorticity is a pseudovector (or axial vector) field that describes the local spinning motion of a continuum near some point (the tendency of something to rotate), as would be seen by an observer located at that point and traveling along with the flow. It is an important quantity in the dynamical theory of fluids and provides a convenient framework for understanding a variety of complex flow phenomena, such as the formation and motion of vortex rings. Mathematically, the vorticity \boldsymbol is the curl of the flow velocity \mathbf v: :\boldsymbol \equiv \nabla \times \mathbf v\,, where \nabla is the nabla operator. Conceptually, \boldsymbol could be determined by marking parts of a continuum in a small neighborhood of the point in question, and watching their ''relative'' displacements as they move along the flow. The vorticity \boldsymbol would be twice the mean angular velocity vector of those particles relative to their center of mass, orie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unsteady Flow
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale geophysical flows involving oceans/atmosphere and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irrotational Flow
In fluid dynamics, potential flow or irrotational flow refers to a description of a fluid flow with no vorticity in it. Such a description typically arises in the limit of vanishing viscosity, i.e., for an inviscid fluid and with no vorticity present in the flow. Potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the curl of the gradient of a scalar always being equal to zero. In the case of an incompressible flow the velocity potential satisfies Laplace's equation, and potential theory is applicable. However, potential flows also have been used to describe compressible flows and Hele-Shaw flows. The potential flow approach occurs in the modeling of both stationary as well as nonstationary flows. Applications of potential flow include ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli's Principle
Bernoulli's principle is a key concept in fluid dynamics that relates pressure, speed and height. For example, for a fluid flowing horizontally Bernoulli's principle states that an increase in the speed occurs simultaneously with a decrease in static pressure, pressure The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book ''Hydrodynamica'' in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form. Bernoulli's principle can be derived from the principle of conservation of energy. This states that, in a steady flow, the sum of all forms of energy in a fluid is the same at all points that are free of viscous forces. This requires that the sum of kinetic energy, potential energy and internal energy remains constant. Thus an increase in the speed of the fluid—implying an increase in its kinetic energy—occur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Velocity
Particle velocity (denoted or ) is the velocity of a particle (real or imagined) in a medium as it transmits a wave. The SI unit of particle velocity is the metre per second (m/s). In many cases this is a longitudinal wave of pressure as with sound, but it can also be a transverse wave as with the vibration of a taut string. When applied to a sound wave through a medium of a fluid like air, particle velocity would be the physical speed of a parcel of fluid as it moves back and forth in the direction the sound wave is travelling as it passes. Particle velocity should not be confused with the speed of the wave as it passes through the medium, i.e. in the case of a sound wave, particle velocity is not the same as the speed of sound. The wave moves relatively fast, while the particles oscillate around their original position with a relatively small particle velocity. Particle velocity should also not be confused with the velocity of individual molecules, which depends mostly on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustic Wave Equation
In physics, the acoustic wave equation is a second-order partial differential equation that governs the propagation of acoustic waves through a material medium resp. a standing wavefield. The equation describes the evolution of acoustic pressure or particle velocity as a function of position and time . A simplified (scalar) form of the equation describes acoustic waves in only one spatial dimension, while a more general form describes waves in three dimensions. For lossy media, more intricate models need to be applied in order to take into account frequency-dependent attenuation and phase speed. Such models include acoustic wave equations that incorporate fractional derivative terms, see also the acoustic attenuation article or the survey paper.S. P. Näsholm and S. Holm, "On a Fractional Zener Elastic Wave Equation," Fract. Calc. Appl. Anal. Vol. 16, No 1 (2013), pp. 26-50, DOI: 10.2478/s13540-013--0003-Link to e-print/ref> Definition in one dimension The wave equation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |