|
Variogram
In spatial statistics the theoretical variogram, denoted 2\gamma(\mathbf_1,\mathbf_2), is a function describing the degree of spatial dependence of a spatial random field or stochastic process Z(\mathbf). The semivariogram \gamma(\mathbf_1,\mathbf_2) is half the variogram. For example, in gold mining, a variogram will give a measure of how much two samples taken from the mining area will vary in gold percentage depending on the distance between those samples. Samples taken far apart will vary more than samples taken close to each other. Definition The semivariogram \gamma(h) was first defined by Matheron (1963) as half the average squared difference between a function and a translated copy of the function separated at distance h. Formally :\gamma(h)=\frac\iiint_V \left (M+h) - f(M) \right2dM, where M is a point in the geometric field V, and f(M) is the value at that point. The triple integral is over 3 dimensions. h is the separation distance (e.g., in meters or km) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kriging
In statistics, originally in geostatistics, kriging or Kriging (), also known as Gaussian process regression, is a method of interpolation based on Gaussian process governed by prior covariances. Under suitable assumptions of the prior, kriging gives the best linear unbiased prediction (BLUP) at unsampled locations. Interpolating methods based on other criteria such as smoothness (e.g., smoothing spline) may not yield the BLUP. The method is widely used in the domain of spatial analysis and computer experiments. The technique is also known as Wiener–Kolmogorov prediction, after Norbert Wiener and Andrey Kolmogorov. The theoretical basis for the method was developed by the French mathematician Georges Matheron in 1960, based on the master's thesis of Danie G. Krige, the pioneering plotter of distance-weighted average gold grades at the Witwatersrand reef complex in South Africa. Krige sought to estimate the most likely distribution of gold based on samples from a few borehol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance Function
In probability theory and statistics, the covariance function describes how much two random variables change together (their ''covariance'') with varying spatial or temporal separation. For a random field or stochastic process ''Z''(''x'') on a domain ''D'', a covariance function ''C''(''x'', ''y'') gives the covariance of the values of the random field at the two locations ''x'' and ''y'': C(x,y) := \operatorname(Z(x),Z(y)) = \mathbb\Big[\big(Z(x)-\mathbb[Z(x)]\big)\big(Z(y)-\mathbb[Z(y)]\big) \Big].\, The same ''C''(''x'', ''y'') is called the autocovariance function in two instances: in time series (to denote exactly the same concept except that ''x'' and ''y'' refer to locations in time rather than in space), and in multivariate random fields (to refer to the covariance of a variable with itself, as opposed to the cross covariance between two different variables at different locations, Cov(''Z''(''x''1), ''Y''(''x''2))). Admissibility For locations ''x''1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Field
In physics and mathematics, a random field is a random function over an arbitrary domain (usually a multi-dimensional space such as \mathbb^n). That is, it is a function f(x) that takes on a random value at each point x \in \mathbb^n(or some other domain). It is also sometimes thought of as a synonym for a stochastic process with some restriction on its index set. That is, by modern definitions, a random field is a generalization of a stochastic process where the underlying parameter need no longer be real or integer valued "time" but can instead take values that are multidimensional vectors or points on some manifold. Formal definition Given a probability space (\Omega, \mathcal, P), an ''X''-valued random field is a collection of ''X''-valued random variables indexed by elements in a topological space ''T''. That is, a random field ''F'' is a collection : \ where each F_t is an ''X''-valued random variable. Examples In its discrete version, a random field is a list of ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlogram
In the analysis of data, a correlogram is a chart of correlation statistics. For example, in time series analysis, a plot of the sample autocorrelations r_h\, versus h\, (the time lags) is an autocorrelogram. If cross-correlation is plotted, the result is called a cross-correlogram. The correlogram is a commonly used tool for checking randomness in a data set. If random, autocorrelations should be near zero for any and all time-lag separations. If non-random, then one or more of the autocorrelations will be significantly non-zero. In addition, correlograms are used in the model identification stage for Box–Jenkins autoregressive moving average time series models. Autocorrelations should be near-zero for randomness; if the analyst does not check for randomness, then the validity of many of the statistical conclusions becomes suspect. The correlogram is an excellent way of checking for such randomness. In multivariate analysis, correlation matrices shown as color-mapp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Process
In probability theory and statistics, a Gaussian process is a stochastic process (a collection of random variables indexed by time or space), such that every finite collection of those random variables has a multivariate normal distribution. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. The concept of Gaussian processes is named after Carl Friedrich Gauss because it is based on the notion of the Gaussian distribution (normal distribution). Gaussian processes can be seen as an infinite-dimensional generalization of multivariate normal distributions. Gaussian processes are useful in statistical modelling, benefiting from properties inherited from the normal distribution. For example, if a random process is modelled as a Gaussian process, the distributions of various derived quantities can be obtained explicitly. Such quanti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geostatistics
Geostatistics is a branch of statistics focusing on spatial or spatiotemporal datasets. Developed originally to predict probability distributions of ore grades for mining operations, it is currently applied in diverse disciplines including petroleum geology, hydrogeology, hydrology, meteorology, oceanography, geochemistry, geometallurgy, geography, forestry, environmental control, landscape ecology, soil science, and agriculture (esp. in precision farming). Geostatistics is applied in varied branches of geography, particularly those involving the spread of diseases (epidemiology), the practice of commerce and military planning (logistics), and the development of efficient spatial networks. Geostatistical algorithms are incorporated in many places, including geographic information systems (GIS). Background Geostatistics is intimately related to interpolation methods but extends far beyond simple interpolation problems. Geostatistical techniques rely on statistical models ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one variable mainly correspond with greater values of the other variable, and the same holds for lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when greater values of one variable mainly correspond to lesser values of the other (that is, the variables tend to show opposite behavior), the covariance is negative. The magnitude of the covariance is the geometric mean of the variances that are in common for the two random variables. The Pearson product-moment correlation coefficient, correlation coefficient normalizes the covariance by dividing by the geometric mean of the total variances for the two random variables. A distinction must be made between (1) the covariance of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
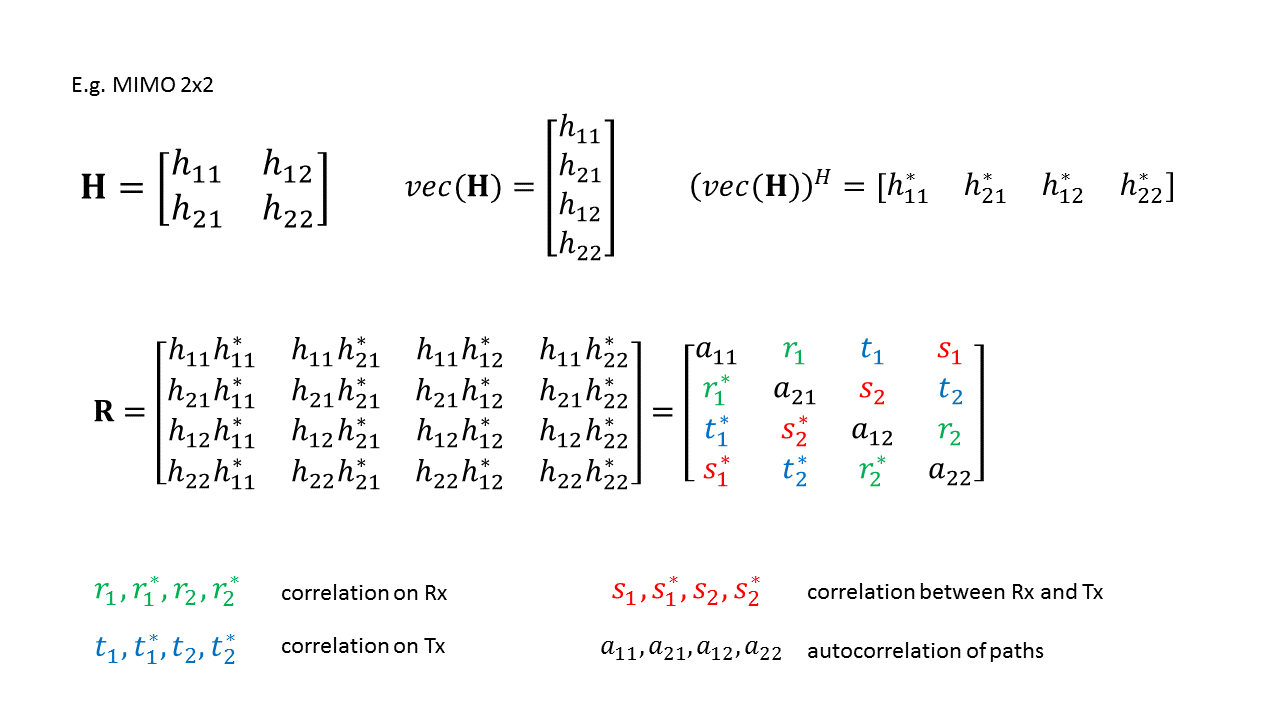
Spatial Correlation
In wireless communication, spatial correlation is the correlation between a signal's spatial direction and the average received signal gain. Theoretically, the performance of wireless communication systems can be improved by having multiple antennas at the transmitter and the receiver. The idea is that if the propagation channels between each pair of transmit and receive antennas are statistically independent and identically distributed, then multiple independent channels with identical characteristics can be created by precoding and be used for either transmitting multiple data streams or increasing the reliability (in terms of bit error rate). In practice, the channels between different antennas are often correlated and therefore the potential multi antenna gains may not always be obtainable. Existence In an ideal communication scenario, there is a line-of-sight path between the transmitter and receiver that represents clear spatial channel characteristics. In urban cell ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Statistics ...
Spatial statistics is a field of applied statistics dealing with spatial data. It involves stochastic processes (random fields, point processes), sampling, smoothing and interpolation, regional ( areal unit) and lattice ( gridded) data, point patterns, as well as image analysis and stereology. See also *Geostatistics *Modifiable areal unit problem *Spatial analysis *Spatial econometrics * Statistical geography *Spatial epidemiology * Spatial network * Statistical shape analysis References {{Statistics-stub Applied statistics Statistics Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Definite
In mathematics, positive definiteness is a property of any object to which a bilinear form In mathematics, a bilinear form is a bilinear map on a vector space (the elements of which are called '' vectors'') over a field ''K'' (the elements of which are called '' scalars''). In other words, a bilinear form is a function that is linea ... or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular: * Positive-definite bilinear form * Positive-definite function * Positive-definite function on a group * Positive-definite functional * Positive-definite kernel * Positive-definite matrix * Positive-definite operator * Positive-definite quadratic form References *. *. {{Set index article, mathematics Quadratic forms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carbon Dioxide In Earth's Atmosphere
In Earth's atmosphere, carbon dioxide is a trace gas that plays an integral part in the greenhouse effect, carbon cycle, photosynthesis and oceanic carbon cycle. It is one of three main greenhouse gases in the atmosphere of Earth. The concentration of carbon dioxide () in the atmosphere reached 427 ppm (0.0427%) on a molar basis in 2024, representing 3341 gigatonnes of . This is an increase of 50% since the start of the Industrial Revolution, up from 280 ppm during the 10,000 years prior to the mid-18th century. The increase is due to human activity. The current increase in concentrations is primarily driven by the burning of fossil fuels.IPCC (2022Summary for policy makers iClimate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA Other significant human activities that emit include cem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |