|
Uzawa Iteration
In numerical mathematics, the Uzawa iteration is an algorithm for solving saddle point problems. It is named after Hirofumi Uzawa and was originally introduced in the context of concave programming. Basic idea We consider a saddle point problem of the form : \begin A & B\\ B^* & \end \begin x_1\\ x_2 \end = \begin b_1\\ b_2 \end, where A is a symmetric positive-definite matrix. Multiplying the first row by B^* A^ and subtracting from the second row yields the upper-triangular system : \begin A & B\\ & -S \end \begin x_1\\ x_2 \end = \begin b_1\\ b_2 - B^* A^ b_1 \end, where S := B^* A^ B denotes the Schur complement. Since S is symmetric positive-definite, we can apply standard iterative methods like the gradient descent method or the conjugate gradient method to solve : S x_2 = B^* A^ b_1 - b_2 in order to compute x_2. The vector x_1 can be reconstructed by solving : A x_1 = b_1 - B x_2. \, It is possible to update x_1 alongside x_2 during the itera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Mathematics
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saddle Point
In mathematics, a saddle point or minimax point is a Point (geometry), point on the surface (mathematics), surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a Critical point (mathematics), critical point), but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction (between peaks) and a relative maxima and minima, maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function f(x,y) = x^2 + y^3 has a critical point at (0, 0) that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the y-direction. The name derives from the fact that the prototypical example in two dimensions is a surface (mathematics), surface that ''curves up'' in one direction, and ''curves down'' in a different dir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hirofumi Uzawa
was a Japanese economist. Biography Uzawa was born on July 21, 1928, in Yonago, Tottori to a farming family. He attended the Tokyo First Middle School (currently the Hibiya High School) and the First Higher School, Japan (now the College of Arts and Sciences, University of Tokyo). He graduated from the Mathematics Department of the University of Tokyo in 1951; he was a special research student from 1951 to 1953. At that time, he discovered the true nature of economics in the words of John Ruskin, “There is no wealth, but life.” which was quoted in the foreword to by Hajime Kawakami, and decided to study economics. His paper on decentralized economic planning caught the eye of Kenneth Arrow at Stanford University. He went to study economics at Stanford University in 1956 with Fulbright fellowship, and became a research assistant, then assistant professor in 1956, then assistant professor at the University of California, Berkeley in 1960, and then associate professor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number \mathbf^* M \mathbf is positive for every nonzero complex column vector \mathbf, where \mathbf^* denotes the conjugate transpose of \mathbf. Positive semi-definite matrices are defined similarly, except that the scalars \mathbf^\mathsf M \mathbf and \mathbf^* M \mathbf are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called ''indefinite''. Some authors use more general definitions of definiteness, permitting the matrices to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schur Complement
The Schur complement is a key tool in the fields of linear algebra, the theory of matrices, numerical analysis, and statistics. It is defined for a block matrix. Suppose ''p'', ''q'' are nonnegative integers such that ''p + q > 0'', and suppose ''A'', ''B'', ''C'', ''D'' are respectively ''p'' × ''p'', ''p'' × ''q'', ''q'' × ''p'', and ''q'' × ''q'' matrices of complex numbers. Let M = \begin A & B \\ C & D \end so that ''M'' is a (''p'' + ''q'') × (''p'' + ''q'') matrix. If ''D'' is invertible, then the Schur complement of the block ''D'' of the matrix ''M'' is the ''p'' × ''p'' matrix defined by M/D := A - BD^C. If ''A'' is invertible, the Schur complement of the block ''A'' of the matrix ''M'' is the ''q'' × ''q'' matrix defined by M/A := D - CA^B. In the case that ''A'' or ''D'' is singular, substituting a generalized inverse for the inverses on ''M/A'' and ''M/D'' yields the generalized Schur complement. The Schur complement is named after Issai Schur who used it to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient Descent
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for minimizing a differentiable multivariate function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a trajectory that maximizes that function; the procedure is then known as ''gradient ascent''. It is particularly useful in machine learning for minimizing the cost or loss function. Gradient descent should not be confused with local search algorithms, although both are iterative methods for optimization. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Gradient Method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-semidefinite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems. The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it. The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems. Description of the problem addres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
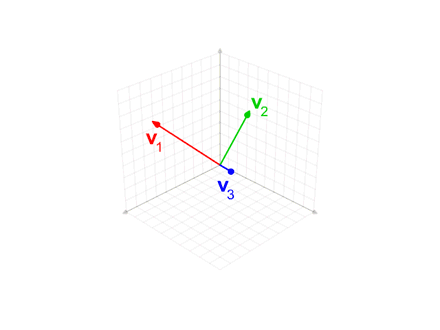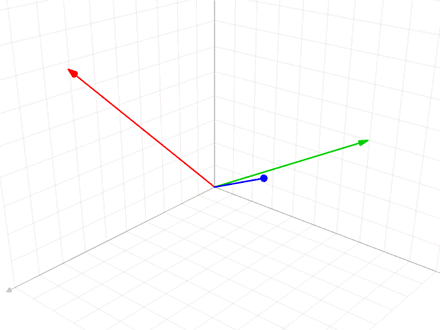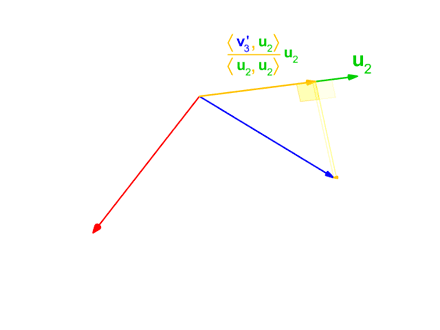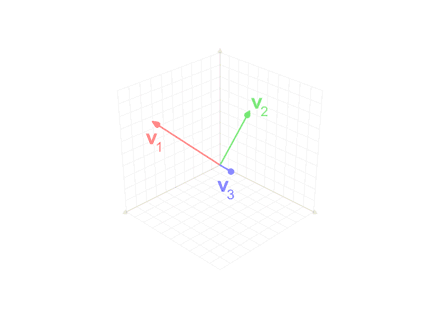
Gram–Schmidt Process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process or Gram-Schmidt algorithm is a way of finding a set of two or more vectors that are perpendicular to each other. By technical definition, it is a method of constructing an orthonormal basis from a set of vector (geometry), vectors in an inner product space, most commonly the Euclidean space \mathbb^n equipped with the standard inner product. The Gram–Schmidt process takes a finite set, finite, linearly independent set of vectors S = \ for and generates an orthogonal set S' = \ that spans the same k-dimensional subspace of \mathbb^n as S. The method is named after Jørgen Pedersen Gram and Erhard Schmidt, but Pierre-Simon Laplace had been familiar with it before Gram and Schmidt. In the theory of Lie group decompositions, it is generalized by the Iwasawa decomposition. The application of the Gram–Schmidt process to the column vectors of a full column rank (linear algebra), rank mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Krylov Subspace
In linear algebra, the order-''r'' Krylov subspace generated by an ''n''-by-''n'' matrix ''A'' and a vector ''b'' of dimension ''n'' is the linear subspace spanned by the images of ''b'' under the first ''r'' powers of ''A'' (starting from A^0=I), that is, :\mathcal_r(A,b) = \operatorname \, \. Background The concept is named after Russian applied mathematician and naval engineer Alexei Krylov, who published a paper about the concept in 1931. Properties * \mathcal_r(A,b), A\,\mathcal_r(A,b)\subset \mathcal_(A,b). * Let r_0 = \operatorname \operatorname \, \. Then \ are linearly independent unless r>r_0, \mathcal_r(A,b) \subset \mathcal_(A,b) for all r, and \operatorname \mathcal_(A,b) = r_0. So r_0 is the maximal dimension of the Krylov subspaces \mathcal_r(A,b). * The maximal dimension satisfies r_0\leq 1 + \operatorname A and r_0 \leq n. * Consider \dim \operatorname \, \ = \deg\,p(A), where p(A) is the minimal polynomial of A. We have r_0\leq \deg\,p(A). Moreover, for an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SIAM Journal On Numerical Analysis
The ''SIAM Journal on Numerical Analysis'' (SINUM; until 1965: ''Journal of the Society for Industrial & Applied Mathematics, Series B: Numerical Analysis'') is a peer-reviewed mathematical journal published by the Society for Industrial and Applied Mathematics that covers research on the analysis of numerical methods. The journal was established in 1964 and appears bimonthly. The editor-in-chief is Angela Kunoth. References External links * Numerical Analysis Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of ... Numerical analysis journals Bimonthly journals Academic journals established in 1964 English-language journals {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |