 |
Urn Problem
In probability and statistics, an urn problem is an idealized mental exercise in which some objects of real interest (such as atoms, people, cars, etc.) are represented as colored balls in an urn or other container. One pretends to remove one or more balls from the urn; the goal is to determine the probability of drawing one color or another, or some other properties. A number of important variations are described below. An urn model is either a set of probabilities that describe events within an urn problem, or it is a probability distribution, or a family of such distributions, of random variables associated with urn problems. History In ''Ars Conjectandi'' (1713), Jacob Bernoulli considered the problem of determining, given a number of pebbles drawn from an urn, the proportions of different colored pebbles within the urn. This problem was known as the ''inverse probability'' problem, and was a topic of research in the eighteenth century, attracting the attention of Abraham ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Lottery
A lottery (or lotto) is a form of gambling that involves the drawing of numbers at random for a prize. Some governments outlaw lotteries, while others endorse it to the extent of organizing a national or state lottery. It is common to find some degree of regulation of lottery by governments. The most common regulations are prohibition of sale to minors and licensing of ticket vendors. Although lotteries were common in the United States and some other countries during the 19th century, by the beginning of the 20th century, most forms of gambling, including lotteries and sweepstakes, were illegal in the U.S. and most of Europe as well as many other countries. This remained so until well after World War II. In the 1960s, casinos and lotteries began to re-appear throughout the world as a means for governments to raise revenue without raising taxes. Lotteries come in many formats. For example, the prize can be a fixed amount of cash or goods. In this format, there is risk to the org ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Geometric Distribution
In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions: * The probability distribution of the number X of Bernoulli trials needed to get one success, supported on \mathbb = \; * The probability distribution of the number Y=X-1 of failures before the first success, supported on \mathbb_0 = \ . These two different geometric distributions should not be confused with each other. Often, the name ''shifted'' geometric distribution is adopted for the former one (distribution of X); however, to avoid ambiguity, it is considered wise to indicate which is intended, by mentioning the support explicitly. The geometric distribution gives the probability that the first occurrence of success requires k independent trials, each with success probability p. If the probability of success on each trial is p, then the probability that the k-th trial is the first success is :\Pr(X = k) = (1-p)^p for k=1,2,3,4,\dots The above form of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Negative Binomial Distribution
In probability theory and statistics, the negative binomial distribution, also called a Pascal distribution, is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified/constant/fixed number of successes r occur. For example, we can define rolling a 6 on some dice as a success, and rolling any other number as a failure, and ask how many failure rolls will occur before we see the third success (r=3). In such a case, the probability distribution of the number of failures that appear will be a negative binomial distribution. An alternative formulation is to model the number of total trials (instead of the number of failures). In fact, for a specified (non-random) number of successes , the number of failures is random because the number of total trials is random. For example, we could use the negative binomial distribution to model the number of days (random) a certain machin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
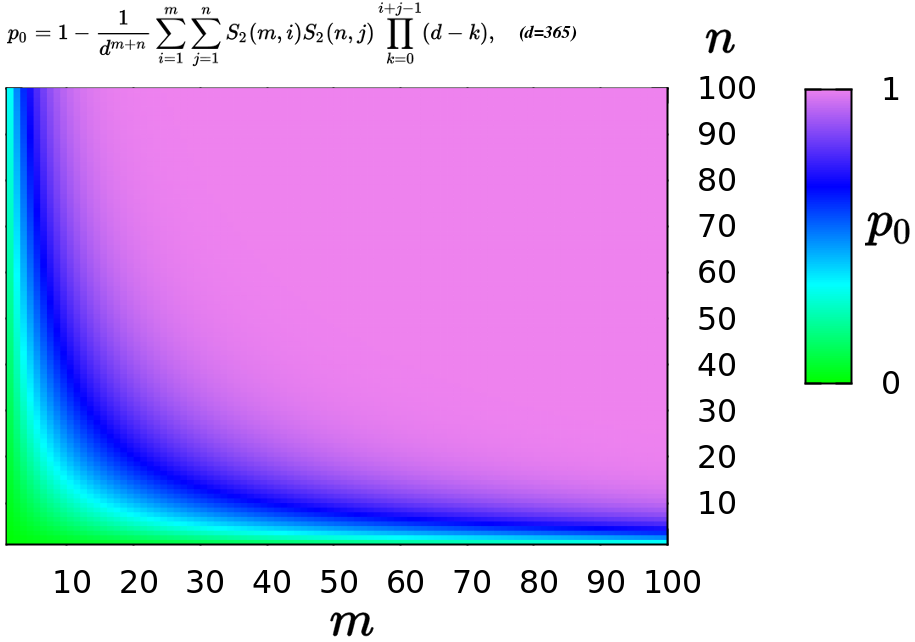 |
Birthday Problem
In probability theory, the birthday problem asks for the probability that, in a set of randomly chosen people, at least two will share the same birthday. The birthday paradox is the counterintuitive fact that only 23 people are needed for that probability to exceed 50%. The birthday paradox is a veridical paradox: it seems wrong at first glance but is, in fact, true. While it may seem surprising that only 23 individuals are required to reach a 50% probability of a shared birthday, this result is made more intuitive by considering that the birthday comparisons will be made between every possible pair of individuals. With 23 individuals, there are = 253 pairs to consider. Real-world applications for the birthday problem include a cryptographic attack called the birthday attack, which uses this probabilistic model to reduce the complexity of finding a Collision attack, collision for a hash function, as well as calculating the approximate risk of a hash collision existi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Coupon Collector's Problem
In probability theory, the coupon collector's problem refers to mathematical analysis of "collect all coupons and win" contests. It asks the following question: if each box of a given product (e.g., breakfast cereals) contains a coupon, and there are ''n'' different types of coupons, what is the probability that more than ''t'' boxes need to be bought to collect all ''n'' coupons? An alternative statement is: given ''n'' coupons, how many coupons do you expect you need to draw with replacement before having drawn each coupon at least once? The mathematical analysis of the problem reveals that the expected number of trials needed grows as \Theta(n\log(n)). For example, when ''n'' = 50 it takes about 225E(50) = 50(1 + 1/2 + 1/3 + ... + 1/50) = 224.9603, the expected number of trials to collect all 50 coupons. The approximation n\log n+\gamma n+1/2 for this expected number gives in this case 50\log 50+50\gamma+1/2 \approx 195.6011+28.8608+0.5\approx 224.9619. trials on ave ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Balls Into Bins Problem
The balls into bins (or balanced allocations) problem is a classic problem in probability theory that has many applications in computer science. The problem involves ''m'' balls and ''n'' boxes (or "bins"). Each time, a single ball is placed into one of the bins. After all balls are in the bins, we look at the number of balls in each bin; we call this number the ''load'' on the bin. The problem can be modelled using a Multinomial distribution, and may involve asking a question such as: What is the expected number of bins with a ball in them? Obviously, it is possible to make the load as small as ''m''/''n'' by putting each ball into the least loaded bin. The interesting case is when the bin is selected at random, or at least partially at random. A powerful balls-into-bins paradigm is the "power of two random choices" where each ball chooses two (or more) random bins and is placed in the lesser-loaded bin. This paradigm has found wide practical applications in shared-memory emulatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Multinomial Distribution
In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts for each side of a ''k''-sided die rolled ''n'' times. For ''n'' statistical independence, independent trials each of which leads to a success for exactly one of ''k'' categories, with each category having a given fixed success probability, the multinomial distribution gives the probability of any particular combination of numbers of successes for the various categories. When ''k'' is 2 and ''n'' is 1, the multinomial distribution is the Bernoulli distribution. When ''k'' is 2 and ''n'' is bigger than 1, it is the binomial distribution. When ''k'' is bigger than 2 and ''n'' is 1, it is the categorical distribution. The term "multinoulli" is sometimes used for the categorical distribution to emphasize this four-way relationship (so ''n'' determines the suffix, and ''k'' the prefix). The Bernoulli distribution models the outcome of a si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Binomial Distribution
In probability theory and statistics, the binomial distribution with parameters and is the discrete probability distribution of the number of successes in a sequence of statistical independence, independent experiment (probability theory), experiments, each asking a yes–no question, and each with its own Boolean-valued function, Boolean-valued outcome (probability), outcome: ''success'' (with probability ) or ''failure'' (with probability ). A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., , the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the binomial test of statistical significance. The binomial distribution is frequently used to model the number of successes in a sample of size drawn with replacement from a population of size . If the sampling is carried out without replacement, the draws ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Sortition
In governance, sortition is the selection of public officer, officials or jurors at random, i.e. by Lottery (probability), lottery, in order to obtain a representative sample. In ancient Athenian democracy, sortition was the traditional and primary method for appointing political officials, and its use was regarded as a principal characteristic of democracy. Sortition is often classified as a method for both direct democracy and deliberative democracy. Today sortition is commonly used to select prospective jurors in common law (legal system), common-law systems. What has changed in recent years is the increased number of citizens' assembly, citizen groups with political advisory power, along with calls for making sortition more consequential than elections, as it was in Athenian democracy, Athens, Republic of Venice, Venice, and Republic of Florence, Florence. History Ancient Athens Athenian democracy developed in the 6th century BC out of what was then called isonomia (equal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Doge Of Venice
The Doge of Venice ( ) – in Italian, was the doge or highest role of authority within the Republic of Venice (697–1797). The word derives from the Latin , meaning 'leader', and Venetian Italian dialect for 'duke', highest official of the republic of Venice for over 1,000 years. In standard Italian, the cognate is '' duce'' ( , ), one of National Fascist Party leader Benito Mussolini's titles. Originally referring to any military leader, it became in the Late Roman Empire the title for a leader of an expeditionary force formed by detachments () from the frontier army (), separate from, but subject to, the governor of a province, authorized to conduct operations beyond provincial boundaries. The Doge of Venice acted as both the head of state and head of the Venetian oligarchy. Doges were elected for life through a complex voting process. History The office and title of doge, in relation to Venetia (region) and Venice (city), emerged from older ducal offices (lat. D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |