|
Universal Code (data Compression)
In data compression, a universal code for integers is a prefix code that maps the positive integers onto binary codewords, with the additional property that whatever the true probability distribution on integers, as long as the distribution is monotonic (i.e., ''p''(''i'') ≥ ''p''(''i'' + 1) for all positive ''i''), the expected lengths of the codewords are within a constant factor of the expected lengths that the optimal code for that probability distribution would have assigned. A universal code is ''asymptotically optimal'' if the ratio between actual and optimal expected lengths is bounded by a function of the information entropy of the code that, in addition to being bounded, approaches 1 as entropy approaches infinity. In general, most prefix codes for integers assign longer codewords to larger integers. Such a code can be used to efficiently communicate a message drawn from a set of possible messages, by simply ordering the set of messages ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Coding
In mathematics and computing, Fibonacci coding is a universal code which encodes positive integers into binary code words. It is one example of representations of integers based on Fibonacci numbers. Each code word ends with "11" and contains no other instances of "11" before the end. The Fibonacci code is closely related to the Zeckendorf representation, a positional numeral system that uses Zeckendorf's theorem and has the property that no number has a representation with consecutive 1s. The Fibonacci code word for a particular integer is exactly the integer's Zeckendorf representation with the order of its digits reversed and an additional "1" appended to the end. Definition For a number N\!, if d(0),d(1),\ldots,d(k-1),d(k)\! represent the digits of the code word representing N\! then we have: : N = \sum_^ d(i) F(i+2),\textd(k-1)=d(k)=1.\! where is the th Fibonacci number, and so is the th distinct Fibonacci number starting with 1,2,3,5,8,13,\ldots. The last bit d(k) i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
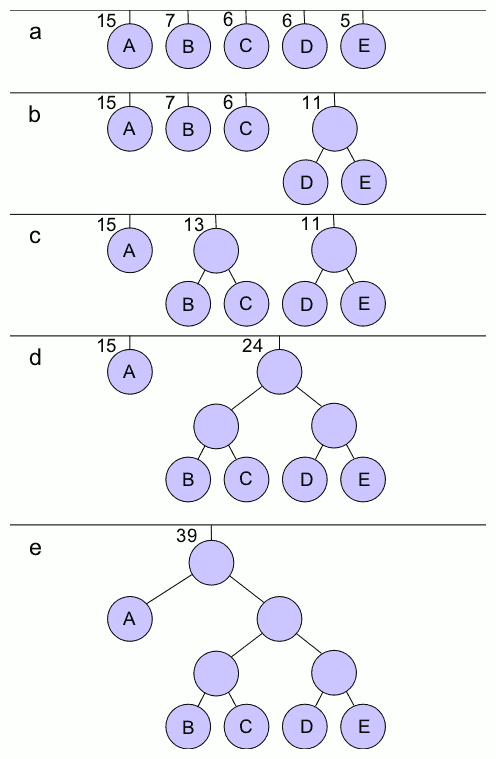
Huffman Coding
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Doctor of Science, Sc.D. student at Massachusetts Institute of Technology, MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes". The output from Huffman's algorithm can be viewed as a variable-length code table for encoding a source symbol (such as a character in a file). The algorithm derives this table from the estimated probability or frequency of occurrence (''weight'') for each possible value of the source symbol. As in other entropy encoding methods, more common symbols are generally represented using fewer bits than less common symbols. Huffman's method can be efficiently implemented, finding a code in time linear time, linear to the number of input weigh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeta Distribution
In probability theory and statistics, the zeta distribution is a discrete probability distribution. If ''X'' is a zeta-distributed random variable with parameter ''s'', then the probability that ''X'' takes the positive integer value ''k'' is given by the probability mass function :f_s(k) = \frac where ''ζ''(''s'') is the Riemann zeta function (which is undefined for ''s'' = 1). The multiplicities of distinct prime factors of ''X'' are independent random variables. The Riemann zeta function being the sum of all terms k^ for positive integer ''k'', it appears thus as the normalization of the Zipf distribution. The terms "Zipf distribution" and "zeta distribution" are often used interchangeably. But while the Zeta distribution is a probability distribution by itself, it is not associated with Zipf's law with the same exponent. Definition The Zeta distribution is defined for positive integers k \geq 1, and its probability mass function is given by : P(x=k) = \frac 1 k^, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauss–Kuzmin Distribution
In mathematics, the Gauss–Kuzmin distribution is a discrete probability distribution that arises as the limit probability distribution of the coefficients in the continued fraction expansion of a random variable uniformly distributed in (0, 1). The distribution is named after Carl Friedrich Gauss, who derived it around 1800, and Rodion Kuzmin, who gave a bound on the rate of convergence in 1929. It is given by the probability mass function : p(k) = - \log_2 \left( 1 - \frac\right)~. Gauss–Kuzmin theorem Let : x = \cfrac be the continued fraction expansion of a random number ''x'' uniformly distributed in (0, 1). Then : \lim_ \mathbb \left\ = - \log_2\left(1 - \frac\right)~. Equivalently, let : x_n = \cfrac~; then : \Delta_n(s) = \mathbb \left\ - \log_2(1+s) tends to zero as ''n'' tends to infinity. Rate of convergence In 1928, Kuzmin gave the bound : , \Delta_n(s), \leq C \exp(-\alpha \sqrt)~. In 1929, Paul Lévy improved it to : , \Delta_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Audio Codec
An audio codec is a device or computer program capable of encoding or decoding a digital data stream (a codec) that encodes or decodes audio. In software, an audio codec is a computer program implementing an algorithm that compresses and decompresses digital audio data according to a given audio file or streaming media audio coding format. The objective of the algorithm is to represent the high-fidelity audio signal with a minimum number of bits while retaining quality. This can effectively reduce the storage space and the bandwidth required for transmission of the stored audio file. Most software codecs are implemented as libraries which interface to one or more multimedia players. Most modern audio compression algorithms are based on modified discrete cosine transform (MDCT) coding and linear predictive coding (LPC). In hardware, audio codec refers to a single device that encodes analog audio as digital signals and decodes digital back into analog. In other words, it contai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
FLAC
FLAC (; Free Lossless Audio Codec) is an audio coding format for lossless compression of digital audio, developed by the Xiph.Org Foundation, and is also the name of the free software project producing the FLAC tools, the reference software package that includes a codec implementation. Digital audio compressed by FLAC's algorithm can typically be reduced to between 50 and 70 percent of its original size and decompresses to an identical copy of the original audio data. FLAC is an open format with royalty-free licensing and a reference implementation which is free software. FLAC supports metadata tagging, album cover art, and fast seeking. History Development was started in 2000 by Josh Coalson. The bitstream format was frozen with the release of version 0.9 of the reference implementation on 31 March 2001. Version 1.0 was released on 20 July 2001. On 29 January 2003, the Xiph.Org Foundation and the FLAC project announced the incorporation of FLAC under the Xiph.org banner. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golomb Coding
Golomb coding is a lossless data compression method using a family of data compression codes invented by Solomon W. Golomb in the 1960s. Alphabets following a geometric distribution will have a Golomb code as an optimal prefix code, making Golomb coding highly suitable for situations in which the occurrence of small values in the input stream is significantly more likely than large values. Rice coding Rice coding (invented by Robert F. Rice) denotes using a subset of the family of Golomb codes to produce a simpler (but possibly suboptimal) prefix code. Rice used this set of codes in an adaptive coding scheme; "Rice coding" can refer either to that adaptive scheme or to using that subset of Golomb codes. Whereas a Golomb code has a tunable parameter that can be any positive integer value, Rice codes are those in which the tunable parameter is a power of two. This makes Rice codes convenient for use on a computer, since multiplication and division by 2 can be implemented ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unary Coding
Unary coding, or the unary numeral system, is an entropy encoding that represents a natural number, ''n'', with ''n'' ones followed by a zero (if the term ''natural number'' is understood as ''non-negative integer'') or with ''n'' − 1 ones followed by a zero (if the term ''natural number'' is understood as ''strictly positive integer''). A unary number's code length would thus be ''n'' + 1 with that first definition, or ''n'' with that second definition. Unary code when vertical behaves like mercury in a thermometer that gets taller or shorter as ''n'' gets bigger or smaller, and so is sometimes called thermometer code. An alternative representation uses ''n'' or ''n'' − 1 zeros followed by a one, effectively swapping the ones and zeros, without loss of generality. For example, the first ten unary codes are: Unary coding is an ''optimally efficient'' encoding for the following discrete probability distribution :\operatorname(n) = 2^\, fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variable-length Quantity
A variable-length quantity (VLQ) is a universal code that uses an arbitrary number of binary octets (eight- bit bytes) to represent an arbitrarily large integer. A VLQ is essentially a base-128 representation of an unsigned integer with the addition of the eighth bit to mark continuation of bytes. VLQ is identical to LEB128 except in endianness. See the example below. Applications and history Base-128 compression is known by many namesVB (Variable Byte), VByte, Varint, VInt, EncInt etc.Jianguo Wang; Chunbin Lin; Yannis Papakonstantinou; Steven Swanson"An Experimental Study of Bitmap Compression vs. Inverted List Compression". 2017. . A variable-length quantity (VLQ) was defined for use in the standard MIDI file formatMIDI File Format: Variable Quantities ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Base 16
Hexadecimal (also known as base-16 or simply hex) is a positional numeral system that represents numbers using a radix (base) of sixteen. Unlike the decimal system representing numbers using ten symbols, hexadecimal uses sixteen distinct symbols, most often the symbols "0"–"9" to represent values 0 to 9 and "A"–"F" to represent values from ten to fifteen. Software developers and system designers widely use hexadecimal numbers because they provide a convenient representation of binary-coded values. Each hexadecimal digit represents four bits (binary digits), also known as a nibble (or nybble). For example, an 8-bit byte is two hexadecimal digits and its value can be written as to in hexadecimal. In mathematics, a subscript is typically used to specify the base. For example, the decimal value would be expressed in hexadecimal as . In programming, several notations denote hexadecimal numbers, usually involving a prefix. The prefix 0x is used in C, which would denote this v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Base 15
There are many different numeral systems, that is, writing systems for expressing numbers. By culture / time period "A ''base'' is a natural number B whose ''powers'' (B multiplied by itself some number of times) are specially designated within a numerical system." The term is not equivalent to radix, as it applies to all numerical notation systems (not just positional ones with a radix) and most systems of spoken numbers. Some systems have two bases, a smaller (subbase) and a larger (base); an example is Roman numerals, which are organized by fives (V=5, L=50, D=500, the subbase) and tens (X=10, C=100, M=1,000, the base). By type of notation Numeral systems are classified here as to whether they use positional notation (also known as place-value notation), and further categorized by radix or base. Standard positional numeral systems The common names are derived Hexadecimal#Etymology, somewhat arbitrarily from a mix of Latin and Greek language, Greek, in some cases incl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |