|
Ungula (primate Anatomy)
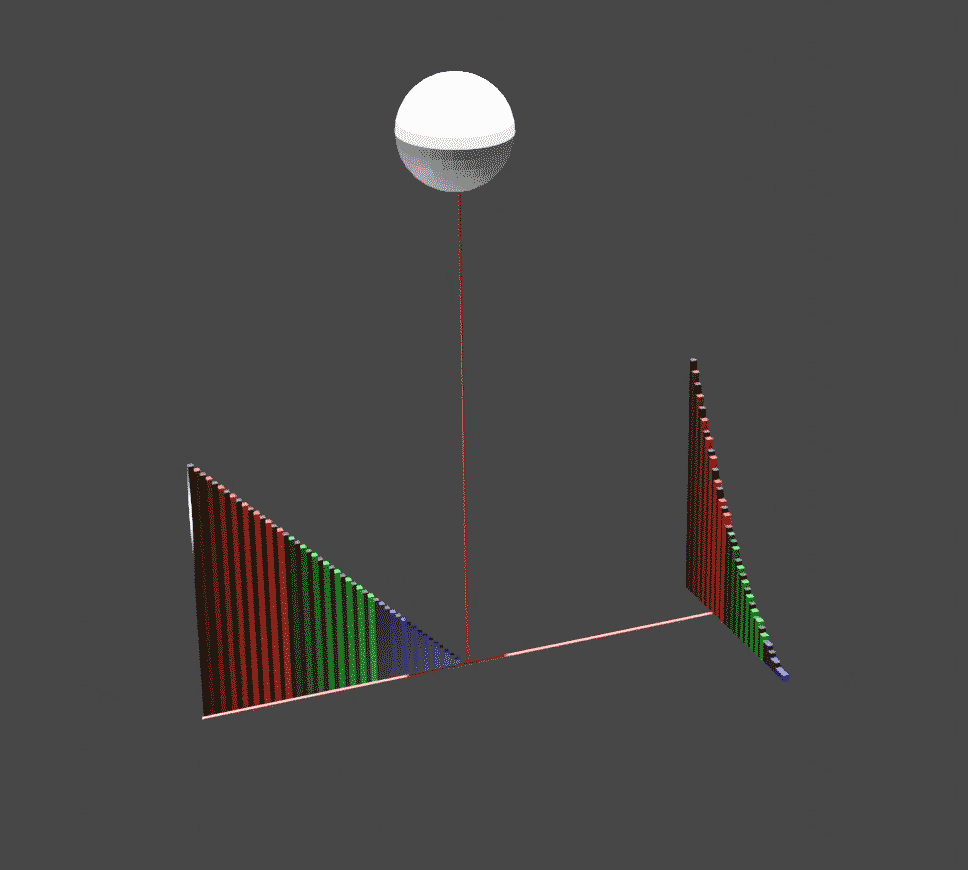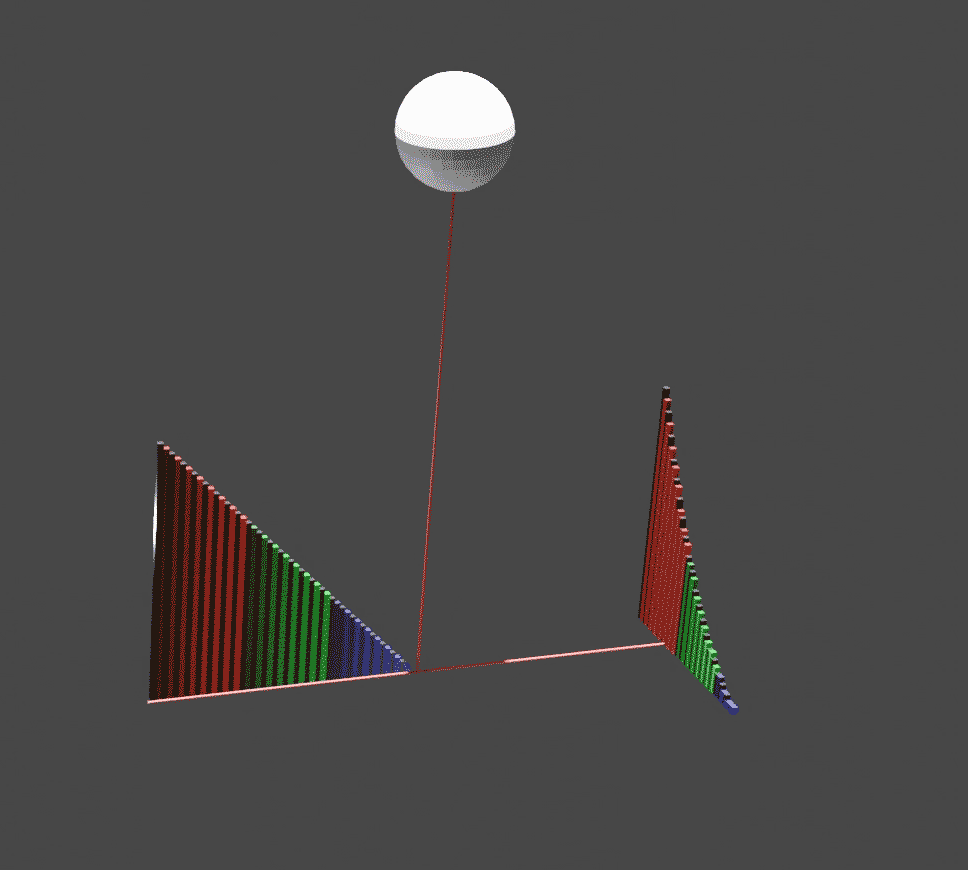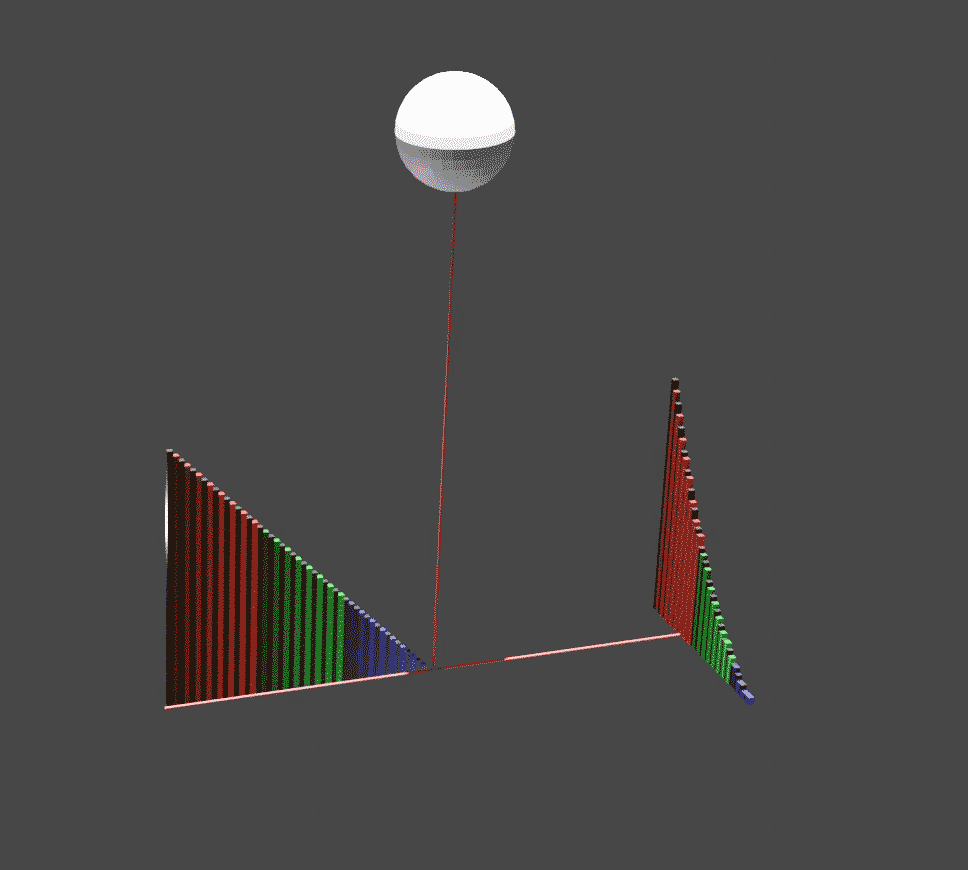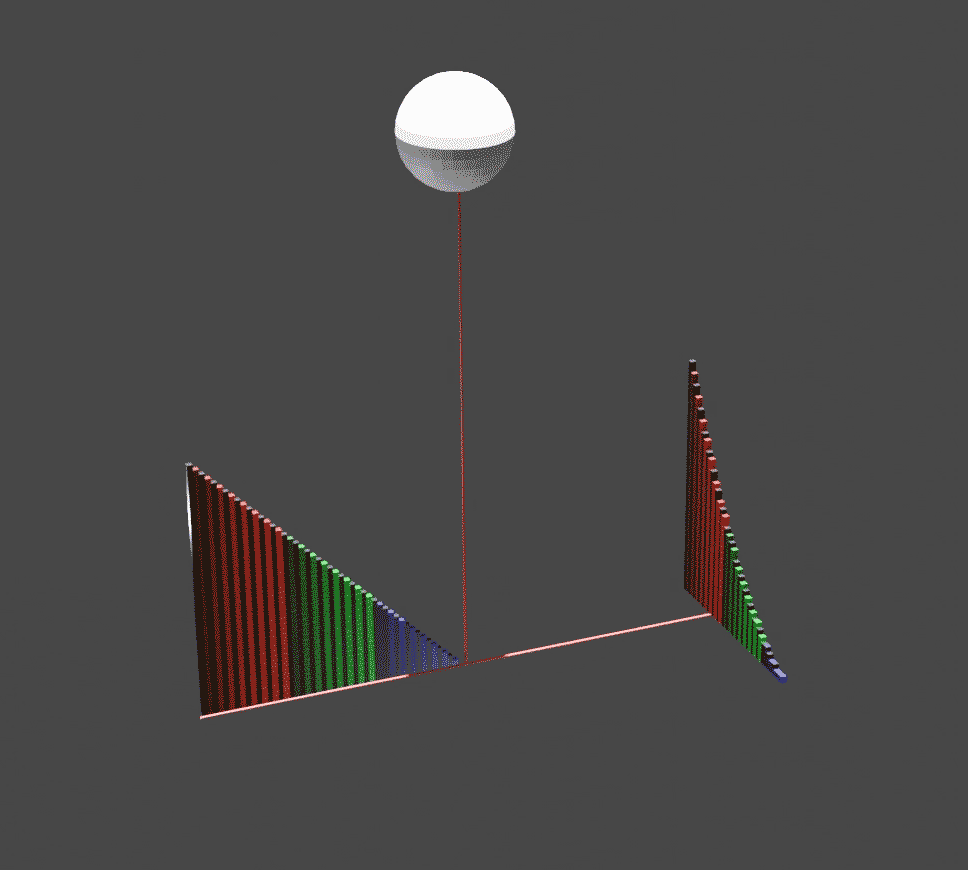
In solid geometry, an ungula is a region of a solid of revolution, cut off by a plane oblique to its base. A common instance is the spherical wedge. The term ''ungula'' refers to the hoof of a horse, an anatomical feature that defines a class of mammals called ungulates. The volume of an ungula of a cylinder was calculated by Grégoire de Saint Vincent. Two cylinders with equal radii and perpendicular axes intersect in four double ungulae.Blaise Pascalbr>Lettre de Dettonville a Carcavidescribes the onglet and double onglet, link from HathiTrust The bicylinder formed by the intersection had been measured by Archimedes in The Method of Mechanical Theorems, but the manuscript was lost until 1906. A historian of calculus described the role of the ungula in integral calculus: :Grégoire himself was primarily concerned to illustrate by reference to the ''ungula'' that volumetric integration could be reduced, through the ''ductus in planum'', to a consideration of geometric relations be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Geometry
Solid geometry or stereometry is the geometry of Three-dimensional space, three-dimensional Euclidean space (3D space). A solid figure is the region (mathematics), region of 3D space bounded by a two-dimensional closed surface; for example, a solid ball (mathematics), ball consists of a sphere and its Interior (topology), interior. Solid geometry deals with the measurements of volumes of various solids, including Pyramid (geometry), pyramids, Prism (geometry), prisms (and other polyhedrons), cubes, Cylinder (geometry), cylinders, cone (geometry), cones (and Frustum, truncated cones). History The Pythagoreanism, Pythagoreans dealt with the regular solids, but the pyramid, prism, cone and cylinder were not studied until the Platonism, Platonists. Eudoxus of Cnidus, Eudoxus established their measurement, proving the pyramid and cone to have one-third the volume of a prism and cylinder on the same base and of the same height. He was probably also the discoverer of a proof that t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Method Of Mechanical Theorems
''The Method of Mechanical Theorems'' (), also referred to as ''The Method'', is one of the major surviving works of the ancient Greece, ancient Greek polymath Archimedes. ''The Method'' takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of method of indivisibles, indivisibles (indivisibles are geometric versions of infinitesimals). The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the Center of mass, center of weights of figures (centroid) and the Lever#Law of the lever, law of the lever, which were demonstrated by Archimedes in ''On the Equilibrium of Planes''. Archimedes did not admit the method of indivisibles as part of rigorous mathematics, and therefore did not publish his method in the formal treatises tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Google Books
Google Books (previously known as Google Book Search, Google Print, and by its code-name Project Ocean) is a service from Google that searches the full text of books and magazines that Google has scanned, converted to text using optical character recognition (OCR), and stored in its digital database.The basic Google book link is found at: https://books.google.com/ . The "advanced" interface allowing more specific searches is found at: https://books.google.com/advanced_book_search Books are provided either by publishers and authors through the Google Books Partner Program, or by Google's library partners through the Library Project. Additionally, Google has partnered with a number of magazine publishers to digitize their archives. The Publisher Program was first known as Google Print when it was introduced at the Frankfurt Book Fair in October 2004. The Google Books Library Project, which scans works in the collections of library partners and adds them to the digital inventory, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steinmetz Solid
In geometry, a Steinmetz solid is the solid body obtained as the intersection of two or three cylinders of equal radius at right angles. Each of the curves of the intersection of two cylinders is an ellipse. The intersection of two cylinders is called a bicylinder. Topologically, it is equivalent to a square hosohedron. The intersection of three cylinders is called a tricylinder. A bisected bicylinder is called a vault, and a cloister vault in architecture has this shape. Steinmetz solids are named after mathematician Charles Proteus Steinmetz, who solved the problem of determining the volume of the intersection. However, the same problem had been solved earlier, by Archimedes in the ancient Greek world, Zu Chongzhi in ancient China, and Piero della Francesca in the early Italian Renaissance. They appear prominently in the sculptures of Frank Smullin. Bicylinder A bicylinder generated by two cylinders with radius has the volume V = \frac r^3, and the surface area ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Wedge
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned ea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conical Ungula
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the ''apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shell Integration
Shell integration (the shell method in integral calculus) is a method for calculating the volume of a solid of revolution, when integrating along an axis ''perpendicular to'' the axis of revolution. This is in contrast to disc integration which integrates along the axis ''parallel'' to the axis of revolution. Definition The shell method goes as follows: Consider a volume in three dimensions obtained by rotating a cross-section in the -plane around the -axis. Suppose the cross-section is defined by the graph of the positive function on the interval . Then the formula for the volume will be: :2 \pi \int_a^b x f(x)\, dx If the function is of the coordinate and the axis of rotation is the -axis then the formula becomes: :2 \pi \int_a^b y f(y)\, dy If the function is rotating around the line then the formula becomes: :\begin \displaystyle 2 \pi \int_a^b (x-h) f(x)\,dx, & \text\ h \le a < b\\ \displaystyle 2 \pi \int_a^b (h-x) f(x)\,dx, & \text\ a < b \le h, \end ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylindrical Ungula
A cylinder () has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base. A cylinder may also be defined as an infinite curvilinear surface in various modern branches of geometry and topology. The shift in the basic meaning—solid versus surface (as in a solid ball versus sphere surface)—has created some ambiguity with terminology. The two concepts may be distinguished by referring to solid cylinders and cylindrical surfaces. In the literature the unadorned term "cylinder" could refer to either of these or to an even more specialized object, the ''right circular cylinder''. Types The definitions and results in this section are taken from the 1913 text ''Plane and Solid Geometry'' by George A. Wentworth and David Eugene Smith . A ' is a surface consisting of all the points on all the lines which are parallel to a given line and which pass through a fixed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elsevier
Elsevier ( ) is a Dutch academic publishing company specializing in scientific, technical, and medical content. Its products include journals such as ''The Lancet'', ''Cell (journal), Cell'', the ScienceDirect collection of electronic journals, ''Trends (journals), Trends'', the ''Current Opinion (Elsevier), Current Opinion'' series, the online citation database Scopus, the SciVal tool for measuring research performance, the ClinicalKey search engine for clinicians, and the ClinicalPath evidence-based cancer care service. Elsevier's products and services include digital tools for Data management platform, data management, instruction, research analytics, and assessment. Elsevier is part of the RELX Group, known until 2015 as Reed Elsevier, a publicly traded company. According to RELX reports, in 2022 Elsevier published more than 600,000 articles annually in over 2,800 journals. As of 2018, its archives contained over 17 million documents and 40,000 Ebook, e-books, with over one b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pergamon Press
Pergamon Press was an Oxford-based publishing house, founded by Paul Rosbaud and Robert Maxwell, that published scientific and medical books and journals. Originally called Butterworth-Springer, it is now an imprint of Elsevier. History The core company, Butterworth-Springer, started in 1948 to bring the "Springer know-how and techniques of aggressive publishing in science"Joe Haines (1988) ''Maxwell'', Houghton Mifflin, p. 137. to Britain. Paul Rosbaud was the man with the knowledge. When Maxwell acquired the company in 1951, Rosbaud held a one-quarter share. They changed the house name to Pergamon Press, using a logo that was a reproduction of a Greek coin from Pergamon. Maxwell and Rosbaud worked together growing the company until May 1956, when, according to Joe Haines, Rosbaud was sacked. When Pergamon Press started it had only six serials and two books. Initially the company headquarters was in Fitzroy Square in West End of London. In 1959, the company moved into He ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margaret Baron
Margaret E. Baron (1915 – 16 August 1996) was a British mathematics educator and historian of mathematics known for her book on the history of calculus. Life Baron was originally from Gateshead, in north-eastern England, and earned a bachelor's degree from Durham University through King's College, Newcastle, which later became Newcastle University. Baron worked for a year as an English teacher in Frankfurt, and in 1938 became a mathematics teacher at the Bede School for Girls, later to become part of Sunderland College. Because she married George Baron, a teacher at the corresponding boys' school, she was dismissed as a teacher in 1940. She took two more teaching posts, at the Royal Grammar School, Newcastle upon Tyne and the High Storrs School in Sheffield, before leaving work to raise her family in Gateshead. Her husband returned from war service in 1946, and they moved to London. Eventually she returned to teaching, at Goldsmiths' College and then, in 1957, as head of m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Calculus
In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an ''antiderivative'', a function whose der ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |