|
Twisting Properties
Twisting properties in general terms are associated with the properties of samples that identify with statistics that are suitable for exchange. Description Starting with a sample \ observed from a random variable ''X'' having a given distribution law with a non-set parameter, a parametric inference problem consists of computing suitable values – call them estimates – of this parameter precisely on the basis of the sample. An estimate is suitable if replacing it with the unknown parameter does not cause major damage in next computations. In algorithmic inference, suitability of an estimate reads in terms of compatibility with the observed sample. In turn, parameter compatibility is a probability measure that we derive from the probability distribution of the random variable to which the parameter refers. In this way we identify a random parameter Θ compatible with an observed sample. Given a sampling mechanism M_X=(g_\theta,Z), the rationale of this operation lies in us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sample (statistics)
In this statistics, quality assurance, and survey methodology, sampling is the selection of a subset or a statistical sample (termed sample for short) of individuals from within a population (statistics), statistical population to estimate characteristics of the whole population. The subset is meant to reflect the whole population, and statisticians attempt to collect samples that are representative of the population. Sampling has lower costs and faster data collection compared to recording data from the entire population (in many cases, collecting the whole population is impossible, like getting sizes of all stars in the universe), and thus, it can provide insights in cases where it is infeasible to measure an entire population. Each observation measures one or more properties (such as weight, location, colour or mass) of independent objects or individuals. In survey sampling, weights can be applied to the data to adjust for the sample design, particularly in stratified samplin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well-behaved Statistic
Although the term well-behaved statistic often seems to be used in the scientific literature in somewhat the same way as is well-behaved in mathematics (that is, to mean "non- pathological") it can also be assigned precise mathematical meaning, and in more than one way. In the former case, the meaning of this term will vary from context to context. In the latter case, the mathematical conditions can be used to derive classes of combinations of distributions with statistics which are ''well-behaved'' in each sense. First Definition: The variance of a well-behaved statistical estimator is finite and one condition on its mean is that it is differentiable in the parameter being estimated. Second Definition: The statistic is monotonic, well-defined, and locally sufficient. Conditions for a Well-Behaved Statistic: First Definition More formally the conditions can be expressed in this way. T is a statistic for \theta that is a function of the sample, _,...,_. For T to be ''well-behaved ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Method Of Moments (statistics)
In statistics, the method of moments is a method of estimation of population parameters. The same principle is used to derive higher moments like skewness and kurtosis. It starts by expressing the population moments (i.e., the expected values of powers of the random variable under consideration) as functions of the parameters of interest. Those expressions are then set equal to the sample moments. The number of such equations is the same as the number of parameters to be estimated. Those equations are then solved for the parameters of interest. The solutions are estimates of those parameters. The method of moments was introduced by Pafnuty Chebyshev in 1887 in the proof of the central limit theorem. The idea of matching empirical moments of a distribution to the population moments dates back at least to Karl Pearson. Method Suppose that the parameter \theta = (\theta_1, \theta_2, \dots, \theta_k) characterizes the distribution f_W(w; \theta) of the random variable W. Supp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fox's H Function
Fox's may refer to: * Fox's Biscuits, a bakery company in the United Kingdom * Fox's Confectionery, a confectioner in the United Kingdom ** Fox's Glacier Mints * Fox's Pizza Den, a pizza restaurant chain See also * {{Disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incomplete Gamma Function
In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals. Their respective names stem from their integral definitions, which are defined similarly to the gamma function but with different or "incomplete" integral limits. The gamma function is defined as an integral from zero to infinity. This contrasts with the lower incomplete gamma function, which is defined as an integral from zero to a variable upper limit. Similarly, the upper incomplete gamma function is defined as an integral from a variable lower limit to infinity. Definition The upper incomplete gamma function is defined as: \Gamma(s,x) = \int_x^ t^\,e^\, dt , whereas the lower incomplete gamma function is defined as: \gamma(s,x) = \int_0^x t^\,e^\, dt . In both cases is a complex parameter, such that the real part of is positive. Properties By integration by parts we find the recurrence relati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
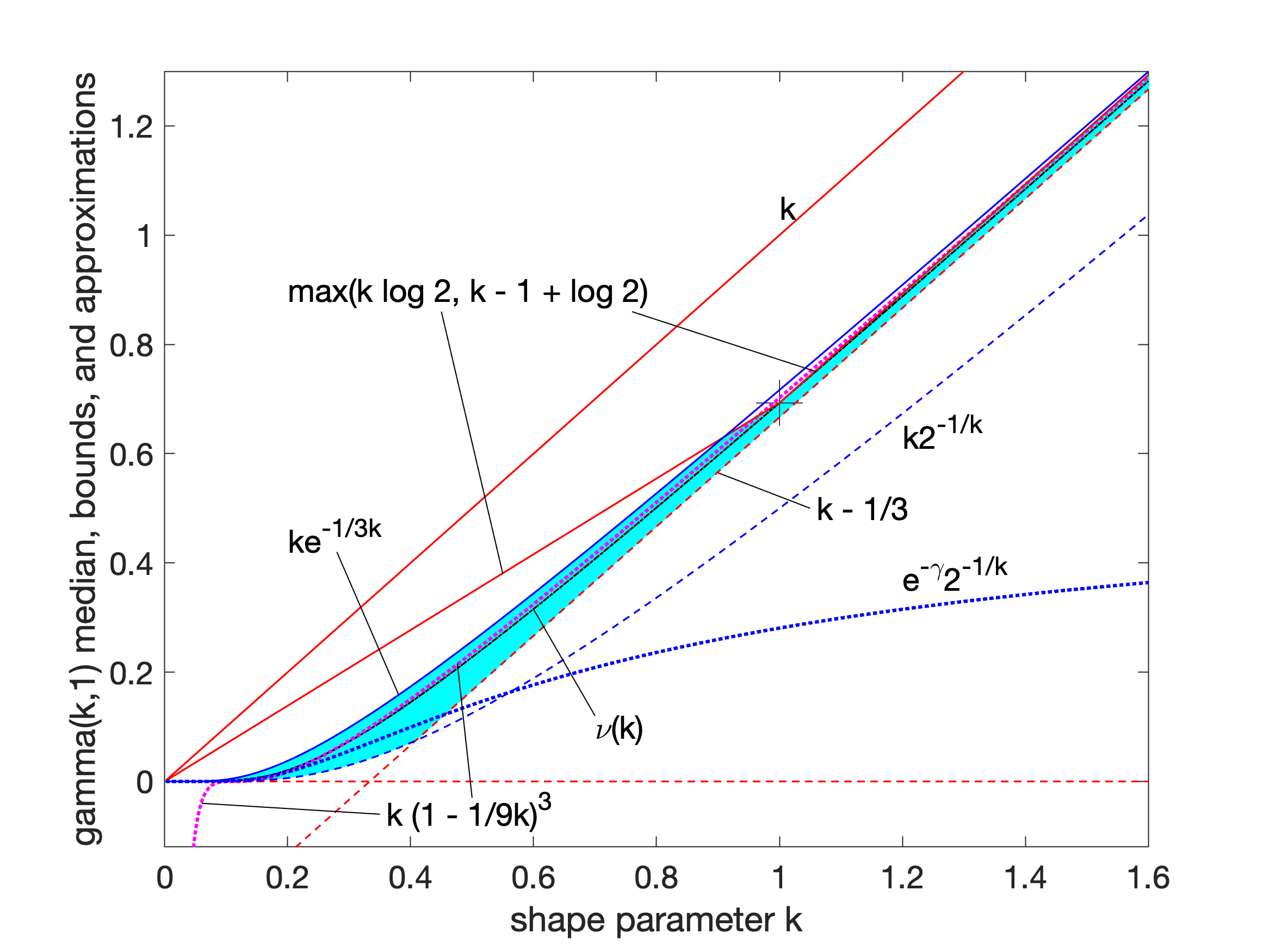
Gamma Distribution
In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: # With a shape parameter and a scale parameter # With a shape parameter \alpha and a rate parameter In each of these forms, both parameters are positive real numbers. The distribution has important applications in various fields, including econometrics, Bayesian statistics, and life testing. In econometrics, the (''α'', ''θ'') parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of an Erlang distribution for integer ''α'' values. Bayesian statisticians prefer the (''α'',''λ'') parameterization, utilizing the gamma distribution as a conjugate prior for several inverse scale parameters, facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fiducial Inference
Fiducial inference is one of a number of different types of statistical inference. These are rules, intended for general application, by which conclusions can be drawn from samples of data. In modern statistical practice, attempts to work with fiducial inference have fallen out of fashion in favour of frequentist inference, Bayesian inference and decision theory. However, fiducial inference is important in the history of statistics since its development led to the parallel development of concepts and tools in theoretical statistics that are widely used. Some current research in statistical methodology is either explicitly linked to fiducial inference or is closely connected to it. Background The general approach of fiducial inference was proposed by Ronald Fisher. Here "fiducial" comes from the Latin for faith. Fiducial inference can be interpreted as an attempt to perform inverse probability without calling on prior probability distributions. Fiducial inference quickly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Master Equation
In physics, chemistry, and related fields, master equations are used to describe the time evolution of a system that can be modeled as being in a probabilistic combination of states at any given time, and the switching between states is determined by a transition rate matrix. The equations are a set of differential equations – over time – of the probabilities that the system occupies each of the different states. The name was proposed in 1940: Introduction A master equation is a phenomenological set of first-order differential equations describing the time evolution of (usually) the probability of a system to occupy each one of a discrete set of states with regard to a continuous time variable ''t''. The most familiar form of a master equation is a matrix form: \frac = \mathbf\vec, where \vec is a column vector, and \mathbf is the matrix of connections. The way connections among states are made determines the dimension of the problem; it is either *a d-dimension ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathematical definition refers to neither randomness nor variability but instead is a mathematical function (mathematics), function in which * the Domain of a function, domain is the set of possible Outcome (probability), outcomes in a sample space (e.g. the set \ which are the possible upper sides of a flipped coin heads H or tails T as the result from tossing a coin); and * the Range of a function, range is a measurable space (e.g. corresponding to the domain above, the range might be the set \ if say heads H mapped to -1 and T mapped to 1). Typically, the range of a random variable is a subset of the Real number, real numbers. Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice, d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well-behaved Statistic
Although the term well-behaved statistic often seems to be used in the scientific literature in somewhat the same way as is well-behaved in mathematics (that is, to mean "non- pathological") it can also be assigned precise mathematical meaning, and in more than one way. In the former case, the meaning of this term will vary from context to context. In the latter case, the mathematical conditions can be used to derive classes of combinations of distributions with statistics which are ''well-behaved'' in each sense. First Definition: The variance of a well-behaved statistical estimator is finite and one condition on its mean is that it is differentiable in the parameter being estimated. Second Definition: The statistic is monotonic, well-defined, and locally sufficient. Conditions for a Well-Behaved Statistic: First Definition More formally the conditions can be expressed in this way. T is a statistic for \theta that is a function of the sample, _,...,_. For T to be ''well-behaved ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |