|
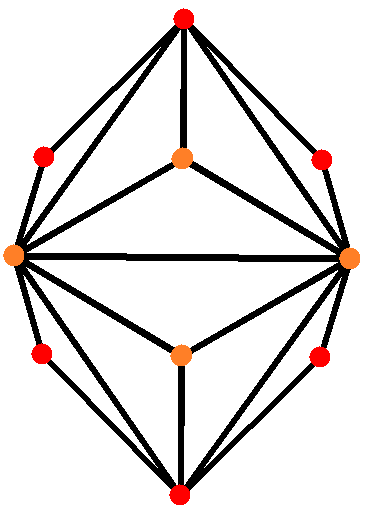
Triakis Octahedron
In geometry, a triakis octahedron (or trigonal trisoctahedron or kisoctahedronConway, Symmetries of things, p. 284) is an Archimedean solid, Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube. It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a ''trisoctahedron'', or, more fully, ''trigonal trisoctahedron''. Both names reflect that it has three triangular faces for every face of an octahedron. The ''tetragonal trisoctahedron'' is another name for the deltoidal icositetrahedron, a different polyhedron with three quadrilateral faces for every face of an octahedron. This convex polyhedron is topologically similar to the concave stellated octahedron. They have the same face connectivity, but the vertices are at different relative distances from the center. If its shorter edges have length of 1, its surface area and volume are: :\begin A &= 3\sqrt \\ V &= \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3-cube T01 B2
A cube or regular hexahedron is a three-dimensional solid object in geometry, which is bounded by six congruent square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with unit side length is the canonical unit of volume in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Triakis Octahedron
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kleetope Of Octahedron
In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope is another polyhedron or polytope formed by replacing each facet of with a pyramid. In some cases, the pyramid is chosen to have regular sides, often producing a non-convex polytope; alternatively, by using sufficiently shallow pyramids, the results may remain convex. Kleetopes are named after Victor Klee,. although the same concept was known under other names long before the work of Klee. Examples In each of these cases, the Kleetope is formed by attaching pyramids onto each face of the original polyhedron. These examples can be seen from the Platonic solids: * The triakis tetrahedron is the Kleetope of a tetrahedron, the triakis octahedron is the Kleetope of an octahedron, and the triakis icosahedron is the Kleetope of an icosahedron. These Kleetopes are formed by adding a triangular pyramid to each face of them. * The tetrakis hexahedron is the Kleetope of the cube, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbifold Notation
In geometry, orbifold notation (or orbifold signature) is a system, invented by the mathematician William Thurston and promoted by John Horton Conway, John Conway, for representing types of symmetry groups in two-dimensional spaces of constant curvature. The advantage of the notation is that it describes these groups in a way which indicates many of the groups' properties: in particular, it follows William Thurston in describing the orbifold obtained by taking the quotient of Euclidean space by the group under consideration. Groups representable in this notation include the point groups in three dimensions, point groups on the sphere (S^2), the frieze groups and wallpaper groups of the Euclidean plane (E^2), and their analogues on the hyperbolic geometry, hyperbolic plane (H^2). Definition of the notation The following types of Euclidean transformation can occur in a group described by orbifold notation: * reflection through a line (or plane) * translation by a vector * rotati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Face-transitive
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its Face (geometry), faces are the same. More specifically, all faces must be not merely Congruence (geometry), congruent but must be ''transitive'', i.e. must lie within the same ''symmetry orbit''. In other words, for any two faces and , there must be a symmetry of the ''entire'' figure by Translation (geometry), translations, Rotation (mathematics), rotations, and/or Reflection (mathematics), reflections that maps onto . For this reason, Convex polytope, convex isohedral polyhedra are the shapes that will make fair dice. Isohedral polyhedra are called isohedra. They can be described by their face configuration. An isohedron has an Parity (mathematics), even number of faces. The Dual polyhedron, dual of an isohedral polyhedron is vertex-transitive, i.e. isogonal. The Catalan solids, the bipyramids, and the trapezo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chronicles Of An Age Of Darkness
''Chronicles of an Age of Darkness'' is a ten-volume series of cross-genre fantasy and science fiction novels created by New Zealand cult author Hugh Cook (science fiction author), Hugh Cook. The series broadly tells of the events leading to the end of a fantasy world's dark age. The ''Chronicles'' are not high fantasy, but could be described as Sword and sorcery or Planetary romance. The novels include elements of science fiction, Comic science fiction, comedy, graphic violence, grotesque and macabre happenings, and political cynicism. They are sometimes described as "Grimdark, gritty" because of their realism. Books *''The Wizards and the Warriors'' (published in the USA as ''Wizard War'') – 1986 () *''The Wordsmiths and the Warguild'' (published in the USA as ''The Questing Hero'' and ''The Hero's Return'') – 1987 () *''The Women and the Warlords'' (published in the USA as ''The Oracle'') – 1987 () *''The Walrus and the Warwolf'' (published in the USA as ''Lords of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hugh Cook (science Fiction Author)
Hugh Walter Gilbert Cook (9 August 1956–8 November 2008) was a cult author, whose works blend fantasy and science fiction. He is best known for his series ''Chronicles of an Age of Darkness''. Biography Cook was born in Billericay in Essex, England in 1956. After spending his early childhood in England, in 1962 he moved to Ocean Island (now known as Banaba) in Kiribati. His experiences of English castles and of life on an equatorial island influenced his writing. In 1964, he moved to New Zealand, where he was educated. He later joined the New Zealand Army as a medic, where he served for ten years, reaching the rank of sergeant. Cook's first novel, ''Plague Summer'', was published in 1980, when he was 24. It concerned drug running in New Zealand during an outbreak of foot and mouth disease. He left the army to write, and published ''The Shift'' in 1986. That comic science fiction novel involved an alien invasion and a machine that altered human history. Under the title ''Aft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3-cube T01
A cube or regular hexahedron is a three-dimensional solid object in geometry, which is bounded by six congruent square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with unit side length is the canonical unit of volume in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |