|
Torricelli's Law
Torricelli's law, also known as Torricelli's theorem, is a theorem in fluid dynamics relating the speed of fluid flowing from a hole to the height of fluid above the hole. The law states that the speed v of efflux of a fluid through a sharp-edged hole in the wall of the tank filled to a height h above the hole is the same as the speed that a body would acquire in falling freely from a height h, v = \sqrt where g is the Gravity of Earth, acceleration due to gravity. This expression comes from equating the kinetic energy gained, \tfrac mv^2, with the potential energy lost, mgh, and solving for v. The law was discovered (though not in this form) by the Italian scientist Evangelista Torricelli, in 1643. It was later shown to be a particular case of Bernoulli's principle. Derivation Under the assumptions of an Incompressible flow, incompressible fluid with negligible viscosity, Bernoulli's principle states that the hydraulic energy is uniform :\frac + \frac + g y_1 = \frac + \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Water Clock
A water clock, or clepsydra (; ; ), is a timepiece by which time is measured by the regulated flow of liquid into (inflow type) or out from (outflow type) a vessel, and where the amount of liquid can then be measured. Water clocks are some of the oldest time-measuring instruments. The simplest form of water clock, with a bowl-shaped outflow, existed in Babylon, Egypt, and Persia around the 16th century BC. Other regions of the world, including India and China, also provide early evidence of water clocks, but the earliest dates are less certain. Water clocks were used in ancient Greece and in ancient Rome, as described by technical writers such as Ctesibius (died 222 BC) and Vitruvius (died after 15 BC). Designs A water clock uses the flow of water to measure time. If viscosity is neglected, the physical principle required to study such clocks is Torricelli's law. Two types of water clock exist: inflow and outflow. In an outflow water clock, a container is filled with wate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oseen Flow
In fluid dynamics, the Oseen equations (or Oseen flow) describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.Batchelor (2000), §4.10, pp. 240–246. Oseen's work is based on the experiments of G.G. Stokes, who had studied the falling of a sphere through a viscous fluid. He developed a correction term, which included inertial factors, for the flow velocity used in Stokes' calculations, to solve the problem known as Stokes' paradox. His approximation leads to an improvement to Stokes' calculations. Equations The Oseen equations are, in case of an object moving with a steady flow velocity U through the fluid—which is at rest far from the object—and in a frame of reference attached to the object: \begin -\rho\mathbf\cdot\nabla\mathbf &= -\nabla p\, +\, \mu \nabla^2 \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Navier–Stokes Equations
The Navier–Stokes equations ( ) are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes). The Navier–Stokes equations mathematically express momentum balance for Newtonian fluids and make use of conservation of mass. They are sometimes accompanied by an equation of state relating pressure, temperature and density. They arise from applying Isaac Newton's second law to fluid motion, together with the assumption that the stress in the fluid is the sum of a diffusing viscous term (proportional to the gradient of velocity) and a pressure term—hence describing ''viscous flow''. The difference between them and the closely related Euler equations is that Navier–Stokes equat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morison Equation
In fluid dynamics the Morison equation is a semi-empirical equation for the inline force on a body in oscillatory flow. It is sometimes called the MOJS equation after all four authors—Morison, O'Brien, Johnson and Schaaf—of the 1950 paper in which the equation was introduced. The Morison equation is used to estimate the wave loads in the design of oil platforms and other offshore structures. Description The Morison equation is the sum of two force components: an inertia force in phase with the local flow acceleration and a drag force proportional to the (signed) square of the instantaneous flow velocity. The inertia force is of the functional form as found in potential flow theory, while the drag force has the form as found for a body placed in a steady flow. In the heuristic approach of Morison, O'Brien, Johnson and Schaaf these two force components, inertia and drag, are simply added to describe the inline force in an oscillatory flow. The transverse force—perpendicular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
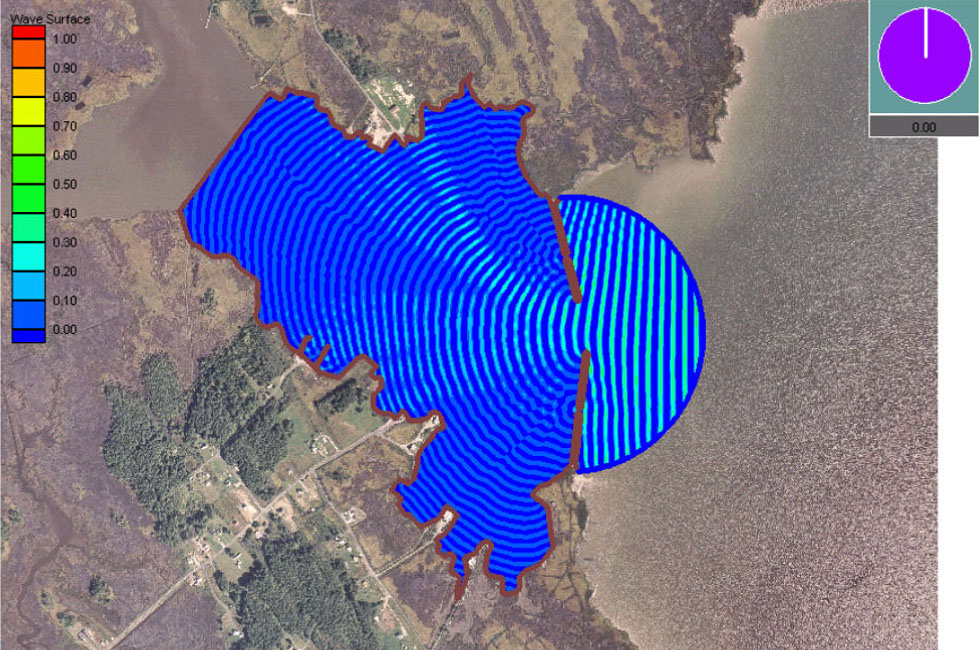
Mild-slope Equation
In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts. The mild-slope equation models the propagation and transformation of water waves, as they travel through waters of varying depth and interact with lateral boundaries such as cliffs, beaches, seawalls and breakwaters. As a result, it describes the variations in wave amplitude, or equivalently wave height. From the wave amplitude, the amplitude of the flow velocity oscillations underneath the water surface can also be computed. These quantities—wave amplitude and flow-velocity amplitude—may subsequently be used to deter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manning Equation
The Manning formula or Manning's equation is an empirical formula estimating the average velocity of a liquid in an open channel flow (flowing in a conduit that does not completely enclose the liquid). However, this equation is also used for calculation of flow variables in case of flow in partially full conduits, as they also possess a free surface like that of open channel flow. All flow in so-called open channels is driven by gravity. It was first presented by the French engineer in 1867, and later re-developed by the Irish engineer Robert Manning in 1890. Thus, the formula is also known in Europe as the Gauckler–Manning formula or Gauckler–Manning–Strickler formula (after Albert Strickler). The Gauckler–Manning formula is used to estimate the average velocity of water flowing in an open channel in locations where it is not practical to construct a weir or flume to measure flow with greater accuracy. Manning's equation is also commonly used as part of a numerica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knudsen Equation
In fluid dynamics, the Knudsen equation is used to describe how gas flows through a tube in free molecular flow. When the mean free path of the molecules in the gas is larger than or equal to the diameter of the tube, the molecules will interact more often with the walls of the tube than with each other. For typical tube dimensions, this occurs only in high or ultrahigh vacuum. The equation was developed by Martin Hans Christian Knudsen (1871–1949), a Danish physicist who taught and conducted research at the Technical University of Denmark The Technical University of Denmark (), often simply referred to as DTU, is a polytechnic university and school of engineering. It was founded in 1829 at the initiative of Hans Christian Ørsted as Denmark's first polytechnic, and it is today ran .... Cylindrical tube For a cylindrical tube, the Knudsen equation is: :q = \frac16 \sqrt \Delta P \frac, where: For nitrogen (or air) at room temperature, the conductivity C (in liters per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kirchhoff Equations
In fluid dynamics, the Kirchhoff equations, named after Gustav Kirchhoff, describe the motion of a rigid body In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible, when a deforming pressure or deforming force is applied on it. The distance between any two given points on a rigid body rema ... in an ideal fluid. \begin & = \times \boldsymbol\omega + \times \mathbf v + \mathbf Q_h + \mathbf Q, \\ 0pt & = \times \boldsymbol\omega + \mathbf F_h + \mathbf F, \\ 0ptT & = \left( \boldsymbol\omega^T \tilde I \boldsymbol\omega + m v^2 \right) \\ 0pt\mathbf Q_h & = -\int p \mathbf x \times\hat\mathbf n \, d\sigma, \\ 0pt\mathbf F_h & = -\int p \hat\mathbf n \, d\sigma \end where \boldsymbol\omega and \mathbf v are the angular and linear velocity vectors at the point \mathbf x, respectively; \tilde I is the moment of inertia tensor, m is the body's mass; \hat\mathbf n is a unit normal vector to the surface o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz's Theorems
In fluid mechanics, Helmholtz's theorems, named after Hermann von Helmholtz, describe the three-dimensional motion of fluid in the vicinity of vortex lines. These theorems apply to inviscid flows and flows where the influence of viscous forces are small and can be ignored. Helmholtz's three theorems are as follows: ;Helmholtz's first theorem: :The strength of a vortex line is constant along its length. ;Helmholtz's second theorem: :A vortex line cannot end in a fluid; it must extend to the boundaries of the fluid or form a closed path. ;Helmholtz's third theorem: :A fluid element that is initially irrotational remains irrotational. Helmholtz's theorems apply to inviscid flows. In observations of vortices in real fluids the strength of the vortices always decays gradually due to the dissipative effect of viscous forces. Alternative expressions of the three theorems are as follows: # The strength of a vortex tube does not vary with time. # Fluid elements lying on a vortex line ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hagen–Poiseuille Equation
In fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Hagen in 1839 and then by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845. The assumptions of the equation are that the fluid is incompressible and Newtonian; the flow is laminar through a pipe of constant circular cross-section that is substantially longer than its diameter; and there is no acceleration of fluid in the pipe. For velocities a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Statics
In physics, a fluid is a liquid, gas, or other material that may continuously move and deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are substances which cannot resist any shear force applied to them. Although the term ''fluid'' generally includes both the liquid and gas phases, its definition varies among branches of science. Definitions of '' solid'' vary as well, and depending on field, some substances can have both fluid and solid properties. Non-Newtonian fluids like Silly Putty appear to behave similar to a solid when a sudden force is applied. Substances with a very high viscosity such as pitch appear to behave like a solid (see pitch drop experiment) as well. In particle physics, the concept is extended to include fluidic matters other than liquids or gases. A fluid in medicine or biology refers to any liquid constituent of the body ( body fluid), whereas "liquid" is not used in this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |