|
Torque Teno Mini Virus 37
In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force (also abbreviated to moment). The symbol for torque is typically \boldsymbol\tau, the lowercase Greek letter ''tau''. When being referred to as moment of force, it is commonly denoted by . Just as a linear force is a push or a pull applied to a body, a torque can be thought of as a twist applied to an object with respect to a chosen point; for example, driving a screw uses torque to force it into an object, which is applied by the screwdriver rotating around its axis to the drives on the head. History The term ''torque'' (from Latin , 'to twist') is said to have been suggested by James Thomson and appeared in print in April, 1884. Usage is attested the same year by Silvanus P. Thompson in the first edition of ''Dynamo-Electric Machinery''. Thompson motivates the term as follows: Today, torque is referred to using different vocabulary depending on g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Force
A force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. The concept of force makes the everyday notion of pushing or pulling mathematically precise. Because the Magnitude (mathematics), magnitude and Direction (geometry, geography), direction of a force are both important, force is a Euclidean vector, vector quantity. The SI unit of force is the newton (unit), newton (N), and force is often represented by the symbol . Force plays an important role in classical mechanics. The concept of force is central to all three of Newton's laws of motion. Types of forces often encountered in classical mechanics include Elasticity (physics), elastic, frictional, Normal force, contact or "normal" forces, and gravity, gravitational. The rotational version of force is torque, which produces angular acceleration, changes in the rotational speed of an object. In an extended body, each part often applies forces on the adjacent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power of the Roman Republic it became the dominant language in the Italian region and subsequently throughout the Roman Empire. Even after the fall of Western Rome, Latin remained the common language of international communication, science, scholarship and academia in Europe until well into the 18th century, when other regional vernaculars (including its own descendants, the Romance languages) supplanted it in common academic and political usage, and it eventually became a dead language in the modern linguistic definition. Latin is a highly inflected language, with three distinct genders (masculine, feminine, and neuter), six or seven noun cases (nominative, accusative, genitive, dative, ablative, and vocative), five declensions, four ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudovector
In physics and mathematics, a pseudovector (or axial vector) is a quantity that is defined as a function of some vectors or other geometric shapes, that resembles a vector, and behaves like a vector in many situations, but is changed into its opposite if the orientation of the space is changed, or an improper rigid transformation such as a reflection is applied to the whole figure. Geometrically, the direction of a reflected pseudovector is opposite to its mirror image, but with equal magnitude. In contrast, the reflection of a ''true'' (or polar) vector is exactly the same as its mirror image. In three dimensions, the curl of a polar vector field at a point and the cross product of two polar vectors are pseudovectors. One example of a pseudovector is the normal to an oriented plane. An oriented plane can be defined by two non-parallel vectors, a and b, [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Of Action
In physics, the line of action (also called line of application) of a force ''(F)'' is a geometric representation of how the force is applied. It is the line through the point at which the force is applied in the same direction as the vector .Mungan, Carl E. "Acceleration of a pulled spool." The Physics Teacher 39.8 (2001): 481-485. https://www.usna.edu/Users/physics/mungan/_files/documents/Publications/TPT.pdf The concept is essential, for instance, for understanding the net effect of multiple forces applied to a body. For example, if two forces of equal magnitude act upon a rigid body along the same line of action but in opposite directions, they cancel and have no net effect. But if, instead, their lines of action are not identical, but merely parallel, then their effect is to create a moment on the body, which tends to rotate it. Calculation of torque For the simple geometry associated with the figure, there are three equivalent equations for the magnitude of the torque ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lever Arm
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of the body. The concept originated with the studies by Archimedes of the usage of levers, which is reflected in his famous quote: "''Give me a lever and a place to stand and I will move the Earth''". Just as a linear force is a push or a pull, a torque can be thought of as a twist to an object around a specific axis. Torque is defined as the product of the magnitude of the perpendicular component of the force and the distance of the line of action of a force from the point around which it is being determined. The law of conservation of energy can also be used to understand torque. The symbol for torque is typically \boldsymbol\tau, the lowercase Greek letter ''tau''. When being referred to as moment of force, it is commonly denoted by . In th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
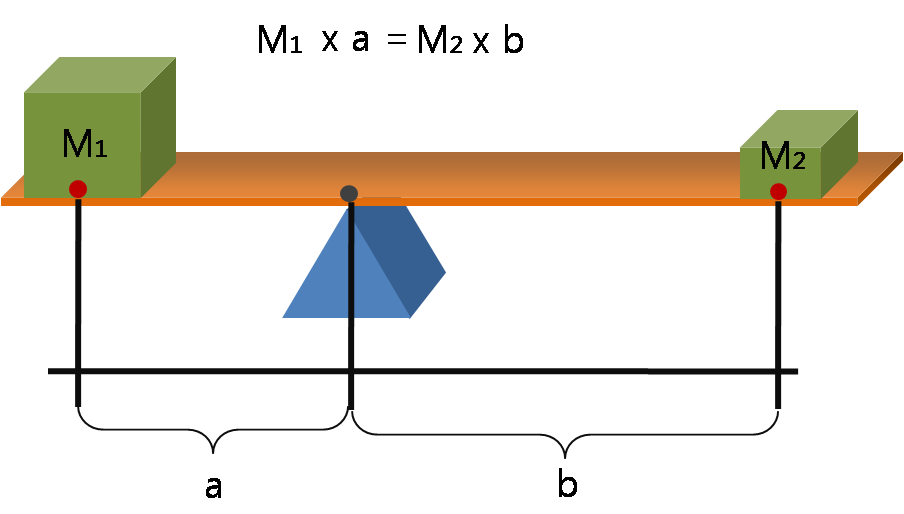
Lever
A lever is a simple machine consisting of a beam or rigid rod pivoted at a fixed hinge, or '' fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, load and effort, the lever is divided into three types. Also, leverage is mechanical advantage gained in a system. It is one of the six simple machines identified by Renaissance scientists. A lever amplifies an input force to provide a greater output force, which is said to provide leverage. The ratio of the output force to the input force is the mechanical advantage of the lever. As such, the lever is a mechanical advantage device, trading off force against movement. Etymology The word "lever" entered English around 1300 from Old French, in which the word was ''levier''. This sprang from the stem of the verb ''lever'', meaning "to raise". The verb, in turn, goes back to the Latin ''levare'', itself from the adjective ''levis'', meaning "light" (as in "not heavy") ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Siméon Denis Poisson
Baron Siméon Denis Poisson FRS FRSE (; 21 June 1781 – 25 April 1840) was a French mathematician and physicist who worked on statistics, complex analysis, partial differential equations, the calculus of variations, analytical mechanics, electricity and magnetism, thermodynamics, elasticity, and fluid mechanics. Moreover, he predicted the Poisson spot in his attempt to disprove the wave theory of Augustin-Jean Fresnel, which was later confirmed. Biography Poisson was born in Pithiviers, Loiret district in France, the son of Siméon Poisson, an officer in the French army. In 1798, he entered the École Polytechnique in Paris as first in his year, and immediately began to attract the notice of the professors of the school, who left him free to make his own decisions as to what he would study. In his final year of study, less than two years after his entry, he published two memoirs, one on Étienne Bézout's method of elimination, the other on the number of integrals of a finit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Engineering
Mechanical engineering is the study of physical machines that may involve force and movement. It is an engineering branch that combines engineering physics and mathematics principles with materials science, to design, analyze, manufacture, and maintain mechanical systems. It is one of the oldest and broadest of the engineering branches. Mechanical engineering requires an understanding of core areas including mechanics, dynamics, thermodynamics, materials science, structural analysis, and electricity. In addition to these core principles, mechanical engineers use tools such as computer-aided design (CAD), computer-aided manufacturing (CAM), and product lifecycle management to design and analyze manufacturing plants, industrial equipment and machinery, heating and cooling systems, transport systems, aircraft, watercraft, robotics, medical devices, weapons, and others. Mechanical engineering emerged as a field during the Industrial Revolution in Europe in the 18 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment (physics)
In physics, a moment is a mathematical expression involving the product of a distance and physical quantity. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. In this way, the moment accounts for the quantity's location or arrangement. For example, the moment of force, often called torque, is the product of a force on an object and the distance from the reference point to the object. In principle, any physical quantity can be multiplied by a distance to produce a moment. Commonly used quantities include forces, masses, and electric charge distributions. Elaboration In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity (such as force or electrical charge) at that point: : \mu_n = r^n\,Q, where Q is the physical quantity such as a force applied at a point, or a point charge, or a point mass, etc. If the quantity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Couple (mechanics)
In mechanics, a couple is a system of forces with a resultant (a.k.a. net or sum) moment of force but no resultant force.''Dynamics, Theory and Applications'' by T.R. Kane and D.A. Levinson, 1985, pp. 90-99Free download/ref> A better term is force couple or pure moment. Its effect is to impart angular momentum but no linear momentum. In rigid body dynamics, force couples are ''free vectors'', meaning their effects on a body are independent of the point of application. The resultant moment of a couple is a ''special case'' of moment. A couple has the property that it is independent of reference point. Simple couple ;Definition A couple is a pair of forces, equal in magnitude, oppositely directed, and displaced by perpendicular distance or moment. The simplest kind of couple consists of two equal and opposite forces whose lines of action do not coincide. This is called a "simple couple".''Dynamics, Theory and Applications'' by T.R. Kane and D.A. Levinson, 1985, pp. 90-99Free ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsion (mechanics)
In the field of solid mechanics, torsion is the twisting of an object due to an applied torque. Torsion is expressed in either the pascal (Pa), an SI unit for newtons per square metre, or in pounds per square inch (psi) while torque is expressed in newton metres (N·m) or foot-pound force (ft·lbf). In sections perpendicular to the torque axis, the resultant shear stress in this section is perpendicular to the radius. In non-circular cross-sections, twisting is accompanied by a distortion called warping, in which transverse sections do not remain plane. For shafts of uniform cross-section unrestrained against warping, the torsion is: : T = \frac \tau= \frac G \varphi where: * ''T'' is the applied torque or moment of torsion in Nm. * \tau (tau) is the maximum shear stress at the outer surface * ''J''T is the torsion constant for the section. For circular rods, and tubes with constant wall thickness, it is equal to the polar moment of inertia of the section, but for other s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |