|
Three-level Lasers
In physics, specifically statistical mechanics, a population inversion occurs when a system (such as a group of atoms or molecules) exists in a state in which more members of the system are in higher, excited states than in lower, unexcited energy states. It is called an "inversion" because in many familiar and commonly encountered physical systems in thermal equilibrium, this is not possible. This concept is of fundamental importance in laser science because the production of a population inversion is a necessary step in the workings of a standard laser. Boltzmann distributions and thermal equilibrium To understand the concept of a population inversion, it is necessary to understand some thermodynamics and the way that light interacts with matter. To do so, it is useful to consider a very simple assembly of atoms forming a laser medium. Assume there is a group of ''N'' atoms, each of which is capable of being in one of two energy states: either # The ''ground state'', with ener ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
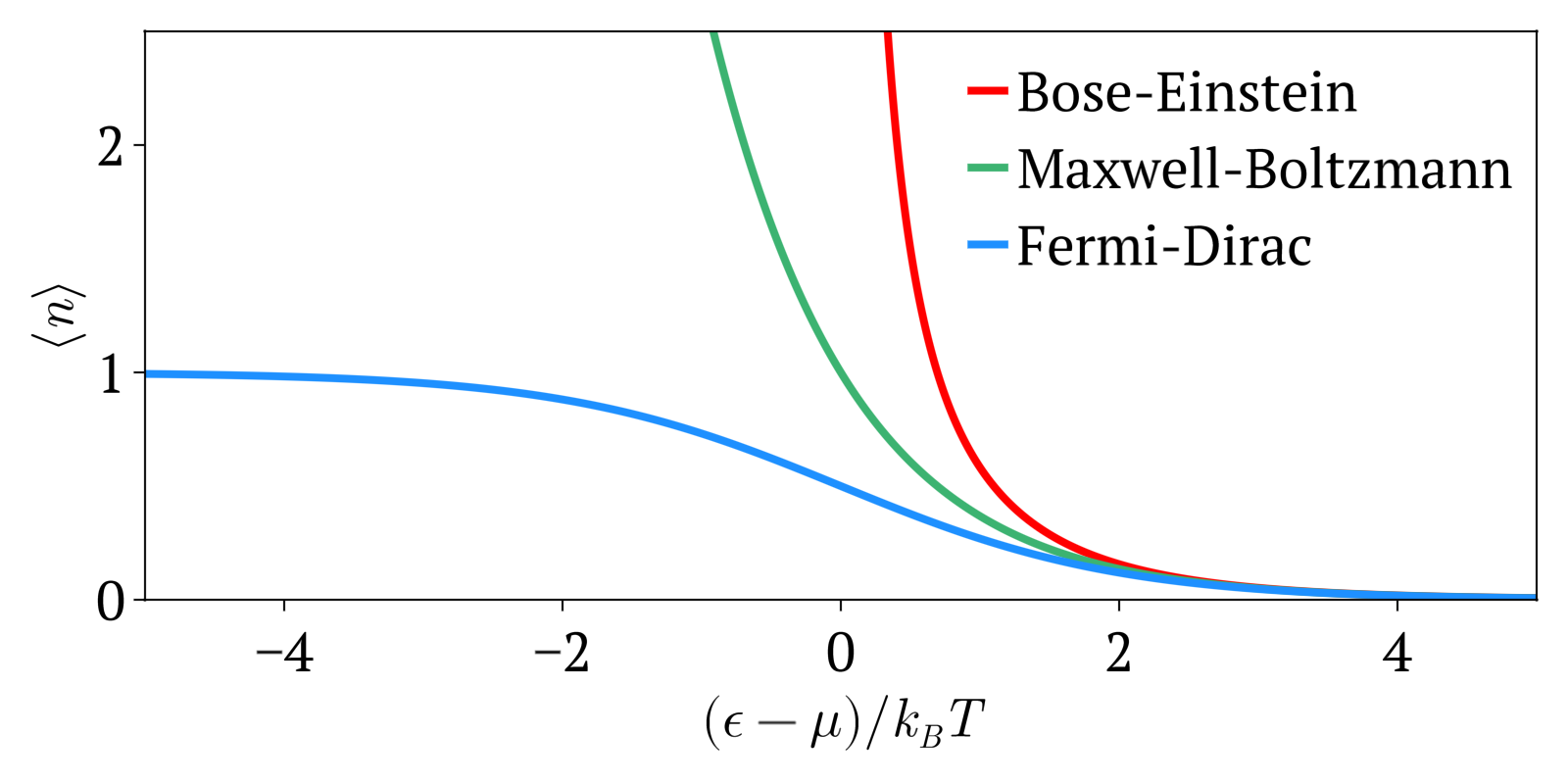 |
Maxwell–Boltzmann Statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density is low enough to render quantum effects negligible. The expected number of particles with energy \varepsilon_i for Maxwell–Boltzmann statistics is : \langle N_i \rangle = \frac = \frac\,g_i e^, where: * \varepsilon_i is the energy of the ''i''th energy level, * \langle N_i \rangle is the average number of particles in the set of states with energy \varepsilon_i, * g_i is the degeneracy of energy level ''i'', that is, the number of states with energy \varepsilon_i which may nevertheless be distinguished from each other by some other means,For example, two simple point particles may have the same energy, but different momentum vectors. They may be distinguished from each other on this basis, and the degeneracy will be the number of po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Stimulated Emission
Stimulated emission is the process by which an incoming photon of a specific frequency can interact with an excited atomic electron (or other excited molecular state), causing it to drop to a lower energy level. The liberated energy transfers to the electromagnetic field, creating a new photon with a frequency, polarization, and direction of travel that are all identical to the photons of the incident wave. This is in contrast to spontaneous emission, which occurs at a characteristic rate for each of the atoms/oscillators in the upper energy state regardless of the external electromagnetic field. According to the American Physical Society, the first person to correctly predict the phenomenon of stimulated emission was Albert Einstein in a series of papers starting in 1916, culminating in what is now called the Einstein B Coefficient. Einstein's work became the theoretical foundation of the maser and the laser. The process is identical in form to atomic absorption in which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Mean Lifetime
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where is the quantity and ( lambda) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant: :\frac = -\lambda N(t). The solution to this equation (see derivation below) is: :N(t) = N_0 e^, where is the quantity at time , is the initial quantity, that is, the quantity at time . Measuring rates of decay Mean lifetime If the decaying quantity, ''N''(''t''), is the number of discrete elements in a certain set, it is possible to compute the average length of time that an element remains in the set. This is called the mean lifetime (or simply the lifetime), where the exponential time constant, \tau, relates to the decay rate constant, λ, in the following way: :\tau = \frac. The mean lifetime can be looke ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Coherence (physics)
Coherence expresses the potential for two waves to Wave interference, interfere. Two Monochromatic radiation, monochromatic beams from a single source always interfere. Wave sources are not strictly monochromatic: they may be ''partly coherent''. When interfering, two waves add together to create a wave of greater amplitude than either one (constructive Wave interference, interference) or subtract from each other to create a wave of minima which may be zero (destructive interference), depending on their relative phase (waves), phase. Constructive or destructive interference are limit cases, and two waves always interfere, even if the result of the addition is complicated or not remarkable. Two waves with constant relative phase will be coherent. The amount of coherence can readily be measured by the interference visibility, which looks at the size of the interference fringes relative to the input waves (as the phase offset is varied); a precise mathematical definition of the de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Phase (waves)
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Stochastic
Stochastic (; ) is the property of being well-described by a random probability distribution. ''Stochasticity'' and ''randomness'' are technically distinct concepts: the former refers to a modeling approach, while the latter describes phenomena; in everyday conversation, however, these terms are often used interchangeably. In probability theory, the formal concept of a '' stochastic process'' is also referred to as a ''random process''. Stochasticity is used in many different fields, including image processing, signal processing, computer science, information theory, telecommunications, chemistry, ecology, neuroscience, physics, and cryptography. It is also used in finance (e.g., stochastic oscillator), due to seemingly random changes in the different markets within the financial sector and in medicine, linguistics, music, media, colour theory, botany, manufacturing and geomorphology. Etymology The word ''stochastic'' in English was originally used as an adjective with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Proportionality (mathematics)
In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio. The ratio is called ''coefficient of proportionality'' (or ''proportionality constant'') and its reciprocal is known as ''constant of normalization'' (or ''normalizing constant''). Two sequences are inversely proportional if corresponding elements have a constant product. Two functions f(x) and g(x) are ''proportional'' if their ratio \frac is a constant function. If several pairs of variables share the same direct proportionality constant, the equation expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio). Proportionality is closely related to ''linearity''. Direct proportionality Given an independent variable ''x'' and a dependent variable ''y'', ''y'' is directly proportional to ''x'' if there is a positive constant ''k'' such that: : y = kx The relation is oft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can move no faster than the speed of light measured in vacuum. The photon belongs to the class of boson particles. As with other elementary particles, photons are best explained by quantum mechanics and exhibit wave–particle duality, their behavior featuring properties of both waves and particles. The modern photon concept originated during the first two decades of the 20th century with the work of Albert Einstein, who built upon the research of Max Planck. While Planck was trying to explain how matter and electromagnetic radiation could be in thermal equilibrium with one another, he proposed that the energy stored within a material object should be regarded as composed of an integer number of discrete, equal-sized parts. To explain the pho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Kelvin
The kelvin (symbol: K) is the base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute temperature scale that starts at the lowest possible temperature (absolute zero), taken to be 0 K. By definition, the Celsius scale (symbol °C) and the Kelvin scale have the exact same magnitude; that is, a rise of 1 K is equal to a rise of 1 °C and vice versa, and any temperature in degrees Celsius can be converted to kelvin by adding 273.15. The 19th century British scientist Lord Kelvin first developed and proposed the scale. It was often called the "absolute Celsius" scale in the early 20th century. The kelvin was formally added to the International System of Units in 1954, defining 273.16 K to be the triple point of water. The Celsius, Fahrenheit, and Rankine scales were redefined in terms of the Kelvin scale using this definition. The 2019 revision of the SI now defines the kelvin in terms of energy by setting the Bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Room Temperature
Room temperature, colloquially, denotes the range of air temperatures most people find comfortable indoors while dressed in typical clothing. Comfortable temperatures can be extended beyond this range depending on humidity, air circulation, and other factors. In certain fields, like science and engineering, and within a particular context, room temperature can mean different agreed-upon ranges. In contrast, ambient temperature is the actual temperature, as measured by a thermometer, of the air (or other medium and surroundings) in any particular place. The ambient temperature (e.g. an unheated room in winter) may be very different from an ideal ''room temperature''. Food and beverages may be served at "room temperature", meaning neither heated nor cooled. Comfort temperatures Comfort temperature is interchangeable with neutral temperature in the scientific literature, which can be calculated through regression analysis between thermal sensation votes and indoor temperature. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Degenerate Energy Levels
In quantum mechanics, an energy level is degenerate if it corresponds to two or more different measurable states of a quantum system. Conversely, two or more different states of a quantum mechanical system are said to be degenerate if they give the same value of energy upon measurement. The number of different states corresponding to a particular energy level is known as the ''degree of degeneracy'' (or simply the ''degeneracy'') of the level. It is represented mathematically by the Hamiltonian for the system having more than one linearly independent eigenstate with the same energy eigenvalue. When this is the case, energy alone is not enough to characterize what state the system is in, and other quantum numbers are needed to characterize the exact state when distinction is desired. In classical mechanics, this can be understood in terms of different possible trajectories corresponding to the same energy. Degeneracy plays a fundamental role in quantum statistical mechanics. For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |