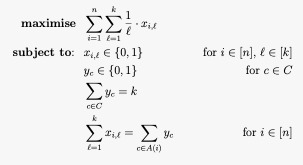|
Thiele's Voting Rules
Thiele's voting rules are rules for multiwinner voting. They allow voters to vote for individual candidates rather than parties, but still guarantee proportional representation. They were published by Thorvald Thiele in Danish in 1895, and translated to English by Svante Janson in 2016. They were used in Swedish parliamentary elections to distribute seats within parties, and are still used in city council elections. Background In multiwinner approval voting, each voter can vote for one or more candidates, and the goal is to select a fixed number ''k'' of winners (where ''k'' may be, for example, the number of parliament members). The question is how to determine the set of winners? * The simplest method is ''multiple non-transferable vote'', in which the ''k'' candidates with the largest number of approvals are elected. But this method tends to select ''k'' candidates of the largest party, leaving the smaller parties with no representation at all. * In the 19th century, ther ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiwinner Voting
Multiwinner or committee voting refers to electoral systems that elect several candidates at once. Such methods can be used to elect parliaments or committees. Goals There are many scenarios in which multiwinner voting is useful. They can be broadly classified into three classes, based on the main objective in electing the committee: # Excellence. Here, voters judge the quality of each candidate individually. The goal is to find the "objectively" best candidates. An example application is shortlisting: selecting, from a list of candidate employees, a small set of finalists, who will proceed to the final stage of evaluation (e.g. using an interview). Here, each candidate is evaluated independently of the others. If two candidates are similar, then probably both will be elected or both will be rejected. # Diversity. Here, the elected candidates should be as ''different'' as possible. For example, suppose the contest is about choosing locations for two fire stations or other fac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportional Approval Voting
Proportional approval voting (PAV) is a proportional electoral system for multiwinner elections. It is a multiwinner approval method that extends the D'Hondt method of apportionment commonly used to calculate apportionments for party-list proportional representation. However, PAV allows voters to support only the candidates they approve of, rather than being forced to approve or reject all candidates on a given party list. In PAV, voters cast approval ballots marking all candidates they approve of; each voter's ballot is then treated as if all candidates on the ballot were on their own "party list." Seats are then apportioned between candidates in a way that ensures all coalitions are represented proportionally. History PAV is a special case of Thiele's voting rule, proposed by Thorvald N. Thiele. It was used in combination with ranked voting in the Swedish elections from 1909 to 1921 for distributing seats within parties and in local elections. PAV was rediscovered by For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phragmen's Voting Rules
Phragmén's voting rules are rules for multiwinner voting. They allow voters to vote for individual candidates rather than parties, but still guarantee proportional representation. They were published by Lars Edvard Phragmén in French and Swedish between 1893 and 1899, and translated to English by Svante Janson in 2016. Background In multiwinner approval voting, each voter can vote for one or more candidates, and the goal is to select a fixed number ''k'' of winners (where ''k'' may be, for example, the number of parliament members). The question is how to determine the set of winners? * The simplest method is ''multiple non-transferable vote'', in which the ''k'' candidates with the largest number of approvals are elected. But this method tends to select ''k'' candidates of the largest party, leaving the smaller parties with no representation at all. * In the 19th century, there was much discussion regarding election systems that could guarantee proportional representatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
House Monotonicity
House monotonicity (also called house-size monotonicity) is a property of apportionment methods. These are methods for allocating seats in a parliament among federal states (or among political parties). The property says that, if the number of seats in the "house" (the parliament) increases, and the method is re-activated, then no state (or party) should have fewer seats than it previously had. A method that fails to satisfy house-monotonicity is said to have the Alabama paradox. In the context of committee elections, house monotonicity is often called committee monotonicity. It says that, if the size of the committee increases, then all the candidate that were previously elected, are still elected. House monotonicity is the special case of ''resource monotonicity'' for the setting in which the resource consists of identical discrete items (the seats). Methods violating house-monotonicity An example of a method violating house-monotonicity is the largest remainder method (= H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ranked Ballot
A ranking is a relationship between a set of items, often recorded in a list, such that, for any two items, the first is either "ranked higher than", "ranked lower than", or "ranked equal to" the second. In mathematics, this is known as a weak order or total preorder of objects. It is not necessarily a total order of objects because two different objects can have the same ranking. The rankings themselves are totally ordered. For example, materials are totally preordered by hardness, while degrees of hardness are totally ordered. If two items are the same in rank it is considered a tie. By reducing detailed measures to a sequence of ordinal numbers, rankings make it possible to evaluate complex information according to certain criteria. Thus, for example, an Internet search engine may rank the pages it finds according to an estimation of their relevance, making it possible for the user quickly to select the pages they are likely to want to see. Analysis of data obtained by ranki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
LiquidFeedback
LiquidFeedback is free software for political opinion formation and decision making. The software incorporates insights from social choice theory in order to aggregate opinions more effectively. Description LiquidFeedback helps groups (such as societies or organizations, political or not) make decisions in an inclusive way, without the limitations of traditional governance methods. It also differs from a general Internet forum by providing a proposition development process that integrates deliberation and voting. LiquidFeedback was originally designed for political parties and other organizations, but has evolved to be used in civic contexts as well. It aims to create an accurate representation of the opinions of the members of the group, without them being distorted by social hierarchies and knowledge differences. Each individual is encouraged to promote his or her own initiatives within the scope set by the operators. This scope may be the democratic self-organization of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequential PAV
Sequential proportional approval voting (SPAV) or reweighted approval voting (RAV) is an electoral system that extends the concept of approval voting to a multiple winner election. It is a simplified version of proportional approval voting. It is a special case of Thiele's voting rules, proposed by Danish statistician Thorvald N. Thiele in the early 1900s. It was used in Sweden from 1909 to 1921, when it was replaced by a "party-list" style system, and is still used for some local elections. Description Sequential proportional approval voting uses approval voting ballots to elect multiple winners on a round-by-round basis. With approval voting ballots, each voter may support any number of candidates on their ballot as they see fit. For tabulation, each ballot is weighted according to a formula, the candidate with the most support is elected, and the process is repeated until there are no more seats to fill. The aforementioned formula is as follows: W=\frac where E is the numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approval Voting
Approval voting is a single-winner rated voting system where voters can approve of all the candidates as they like instead of Plurality voting, choosing one. The method is designed to eliminate vote-splitting while keeping election administration simple and Summability criterion, easy-to-count (requiring only a single score for each candidate). Approval voting has been used in both organizational and political elections to improve representativeness and voter satisfaction. Critics of approval voting have argued the simple ballot format is a disadvantage, as it forces a Dichotomous preferences, binary choice for each candidate (instead of the expressive grades of other rated voting rules). Effect on elections Research by Social choice theory, social choice theorists Steven Brams and Dudley R. Herschbach found that approval voting would increase voter participation, prevent minor-party candidates from being spoiler effect, spoilers, and reduce negative campaigning. Brams' researc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weighted Voting
Weighted voting are voting rules that grant some voters a greater influence than others (which contrasts with rules that assign every voter an equal vote). Examples include publicly-traded companies (which typically grant stockholders one vote for each share they own), as well as the European Council, where the number of votes of each member state is roughly proportional to the square root of the population. Historical examples Ancient Rome The Roman assemblies provided for weighted voting after the person's tribal affiliation and social class (i.e. wealth). Rather than counting one vote per citizen, the assemblies convened in blocs (tribes or centuries), with the plurality of voters in each bloc deciding the vote of the bloc as an entity (which candidate to support or whether to favor or reject a law, for instance). Men of certain tribes and a higher social standing convened in smaller blocs, thus giving their individual vote the effect of many poor citizens' votes. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greedy Algorithm
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time. For example, a greedy strategy for the travelling salesman problem (which is of high computational complexity) is the following heuristic: "At each step of the journey, visit the nearest unvisited city." This heuristic does not intend to find the best solution, but it terminates in a reasonable number of steps; finding an optimal solution to such a complex problem typically requires unreasonably many steps. In mathematical optimization, greedy algorithms optimally solve combinatorial problems having the properties of matroids and give constant-factor approximations to optimization problems with the submodular structure. Specifics Greedy algori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-hard
In computational complexity theory, a computational problem ''H'' is called NP-hard if, for every problem ''L'' which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from ''L'' to ''H''. That is, assuming a solution for ''H'' takes 1 unit time, ''H''s solution can be used to solve ''L'' in polynomial time. As a consequence, finding a polynomial time algorithm to solve a single NP-hard problem would give polynomial time algorithms for all the problems in the complexity class NP. As it is suspected, but unproven, that P≠NP, it is unlikely that any polynomial-time algorithms for NP-hard problems exist. A simple example of an NP-hard problem is the subset sum problem. Informally, if ''H'' is NP-hard, then it is at least as difficult to solve as the problems in NP. However, the opposite direction is not true: some problems are undecidable, and therefore even more difficult to solve than all problems in NP, but they are probably not NP- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |