|
Thermal Conductivity Measurement
There are a number of possible ways to measure thermal conductivity, each of them suitable for a limited range of materials, depending on the thermal properties and the medium temperature. Three classes of methods exist to measure the thermal conductivity of a sample: steady-state, time-domain, and frequency-domain methods. Steady-state methods In general, steady-state techniques perform a measurement when the temperature of the material measured does not change with time. This makes the signal analysis straightforward (steady state implies constant signals). The disadvantage is that a well-engineered experimental setup is usually needed. Steady-state methods, in general, work by applying a known heat flux, \dot Q (W/m^2), to a sample with a surface area, A(m^2) , and thickness, x (m); once the sample's steady-state temperature is reached, the difference in temperature, \Delta T, across the thickness of the sample is measured. After assuming one-dimensional heat flow and an isotrop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Conductivity
The thermal conductivity of a material is a measure of its ability to heat conduction, conduct heat. It is commonly denoted by k, \lambda, or \kappa and is measured in W·m−1·K−1. Heat transfer occurs at a lower rate in materials of low thermal conductivity than in materials of high thermal conductivity. For instance, metals typically have high thermal conductivity and are very efficient at conducting heat, while the opposite is true for insulating materials such as mineral wool or Styrofoam. Metals have this high thermal conductivity due to free electrons facilitating heat transfer. Correspondingly, materials of high thermal conductivity are widely used in heat sink applications, and materials of low thermal conductivity are used as thermal insulation. The reciprocal of thermal conductivity is called thermal resistivity. The defining equation for thermal conductivity is \mathbf = - k \nabla T, where \mathbf is the heat flux, k is the thermal conductivity, and \nabla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kelvin
The kelvin (symbol: K) is the base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute temperature scale that starts at the lowest possible temperature (absolute zero), taken to be 0 K. By definition, the Celsius scale (symbol °C) and the Kelvin scale have the exact same magnitude; that is, a rise of 1 K is equal to a rise of 1 °C and vice versa, and any temperature in degrees Celsius can be converted to kelvin by adding 273.15. The 19th century British scientist Lord Kelvin first developed and proposed the scale. It was often called the "absolute Celsius" scale in the early 20th century. The kelvin was formally added to the International System of Units in 1954, defining 273.16 K to be the triple point of water. The Celsius, Fahrenheit, and Rankine scales were redefined in terms of the Kelvin scale using this definition. The 2019 revision of the SI now defines the kelvin in terms of energy by setting the Bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resistance Temperature Detector
Resistance thermometers, also called resistance temperature detectors (RTDs), are sensors used to measure temperature. Many RTD elements consist of a length of fine wire wrapped around a heat-resistant ceramic or glass core but other constructions are also used. The RTD wire is a pure material, typically platinum (Pt), nickel (Ni), or copper (Cu). The material has an accurate resistance/temperature relationship which is used to provide an indication of temperature. As RTD elements are fragile, they are often housed in protective probes. RTDs, which have higher accuracy and repeatability, are slowly replacing thermocouples in industrial applications below 600 °Celsius, C. Resistance/temperature relationship of metals Common RTD sensing elements for biomedical application constructed of platinum (Pt), nickel (Ni), or copper (Cu) have a repeatability, repeatable, resistance versus temperature relationship (''R'' vs ''T'') and operating temperature range. The ''R'' vs ''T'' re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3ω-method
The 3ω-method (3 omega method) or 3ω-technique, is a measurement method for determining the thermal conductivities of bulk material (i.e. solid or liquid) and thin layers. The process involves a metal heater applied to the sample that is heated periodically. The temperature oscillations thus produced are then measured. The thermal conductivity and thermal diffusivity of the sample can be determined from their frequency dependence. The process was first published by David Cahill and Robert Otto Pohl in 1987 in a paper titled "Thermal Conductivity of Amorphous Solids above the Plateau" in ''Physical Review''. Theory The 3ω-method can be accomplished by depositing a thin metal structure (generally a wire or a film) onto the sample to function as a resistive heater and a resistance temperature detector (RTD). The heater is driven with AC current at frequency ω, which induces periodic joule heating at frequency 2ω (since P = I^R) due to the oscillation of the AC signal during a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be used: \rho = \frac, where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate this quantity is more specifically called specific weight. For a pure substance, the density is equal to its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium is the densest known element at standard conditions for temperature and pressure. To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative den ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kilogram
The kilogram (also spelled kilogramme) is the base unit of mass in the International System of Units (SI), equal to one thousand grams. It has the unit symbol kg. The word "kilogram" is formed from the combination of the metric prefix kilo- (meaning one thousand) and gram; it is colloquially shortened to "kilo" (plural "kilos"). The kilogram is an SI base unit, defined ultimately in terms of three defining constants of the SI, namely a specific transition frequency of the caesium-133 atom, the speed of light, and the Planck constant. A properly equipped metrology laboratory can calibrate a mass measurement instrument such as a Kibble balance as a primary standard for the kilogram mass. The kilogram was originally defined in 1795 during the French Revolution as the mass of one litre of water (originally at 0 °C, later changed to the temperature of its maximum density, approximately 4 °C). The current definition of a kilogram agrees with this original defini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joule
The joule ( , or ; symbol: J) is the unit of energy in the International System of Units (SI). In terms of SI base units, one joule corresponds to one kilogram- metre squared per second squared One joule is equal to the amount of work done when a force of one newton displaces a body through a distance of one metre in the direction of that force. It is also the energy dissipated as heat when an electric current of one ampere passes through a resistance of one ohm for one second. It is named after the English physicist James Prescott Joule (1818–1889). Definition According to the International Bureau of Weights and Measures the joule is defined as "the work done when the point of application of 1 MKS unit of force ewtonmoves a distance of 1 metre in the direction of the force." In terms of SI base units and in terms of SI derived units with special names, the joule is defined as One joule is also equivalent to any of the following: * The work required to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
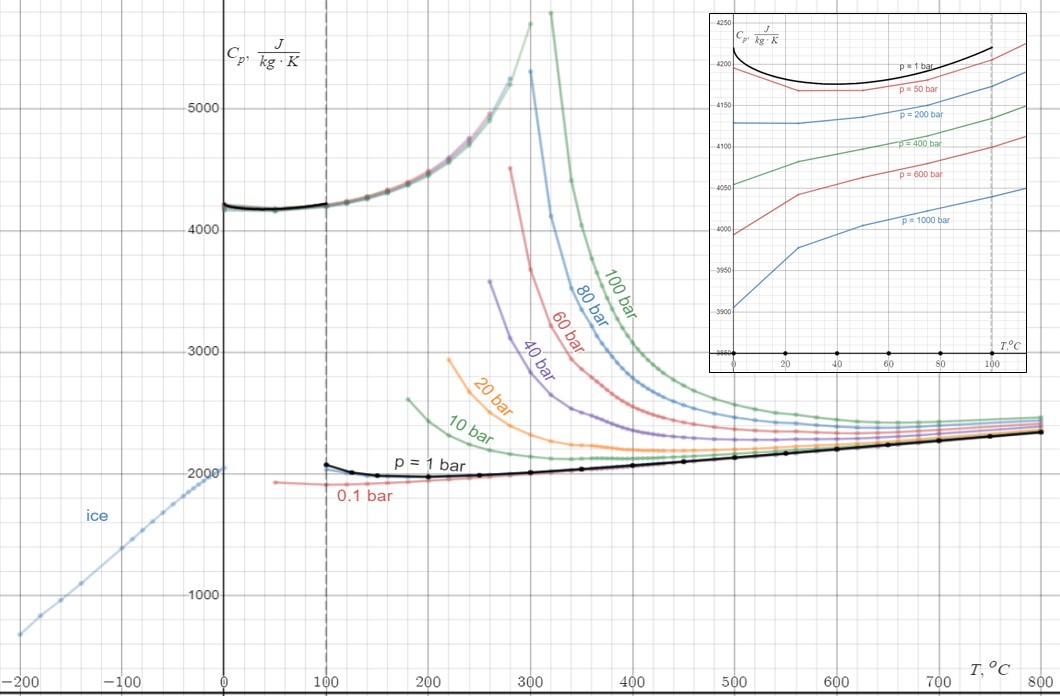
Heat Capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K). Heat capacity is an extensive property. The corresponding intensive property is the specific heat capacity, found by dividing the heat capacity of an object by its mass. Dividing the heat capacity by the amount of substance in moles yields its molar heat capacity. The volumetric heat capacity measures the heat capacity per volume. In architecture and civil engineering, the heat capacity of a building is often referred to as its '' thermal mass''. Definition Basic definition The heat capacity of an object, denoted by C, is the limit C = \lim_\frac, where \Delta Q is the amount of heat that must be added to the object (of mass ''M'') in order to raise its temperature by \Delta T. The value of this parameter usually varies considerably depending o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laser Flash Method
The laser flash analysis or laser flash method is used to measure thermal diffusivity of a variety of different materials. An energy pulse heats one side of a plane-parallel sample and the resulting time dependent temperature rise on the backside due to the energy input is detected. The higher the thermal diffusivity of the sample, the faster the energy reaches the backside. A laser flash apparatus (LFA) to measure thermal diffusivity over a broad temperature range, is shown on the right hand side. In a one-dimensional, adiabatic, adiabatic case the thermal diffusivity a is calculated from this temperature rise as follows: : a = 0.1388 \cdot \frac Where * a is the thermal diffusivity in cm2/s * d is the thickness of the sample in cm * t_ is the time to the half maximum in s As the coefficient 0.1388 is dimensionless, the formula works also for a and d in their corresponding SI units. Measurement principle The laser flash method was developed by Parker et al. in 1961. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geothermal Heat Pump
A ground source heat pump (also geothermal heat pump) is a heating/cooling system for buildings that use a type of heat pump to transfer heat to or from the ground, taking advantage of the relative constancy of temperatures of the earth through the seasons. Ground-source heat pumps (GSHPs)or geothermal heat pumps (GHP), as they are commonly termed in North Americaare among the most energy-efficient technologies for providing HVAC and water heating, using less energy than can be achieved by use of resistive electric heaters. Efficiency is given as a coefficient of performance (CoP) which is typically in the range 3-6, meaning that the devices provide 3-6 units of heat for each unit of electricity used. Setup costs are higher than for other heating systems, due to the requirement of installing ground loops over large areas or of drilling bore holes, hence ground source is often installed when new blocks of flats are built. Air-source heat pumps have lower set-up costs but have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if the base is implicit, simply . Parentheses are sometimes added for clarity, giving , , or . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity. The natural logarithm of is the exponentiation, power to which would have to be raised to equal . For example, is , because . The natural logarithm of itself, , is , because , while the natural logarithm of is , since . The natural logarithm can be defined for any positive real number as the Integral, area under the curve from to (with the area being negative when ). The simplicity of this definition, which is matched in many other formulas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler–Mascheroni Constant
Euler's constant (sometimes called the Euler–Mascheroni constant) is a mathematical constant, usually denoted by the lowercase Greek letter gamma (), defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by : \begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,\mathrm dx. \end Here, represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43), where he described it as "worthy of serious consideration". Euler initially calculated the constant's value to 6 decimal places. In 1781, he calculated it to 16 decimal places. Euler used the notations and for the constant. The Italian mathematician Lorenzo Mascheroni attempted to calculate the constant to 32 dec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |