|
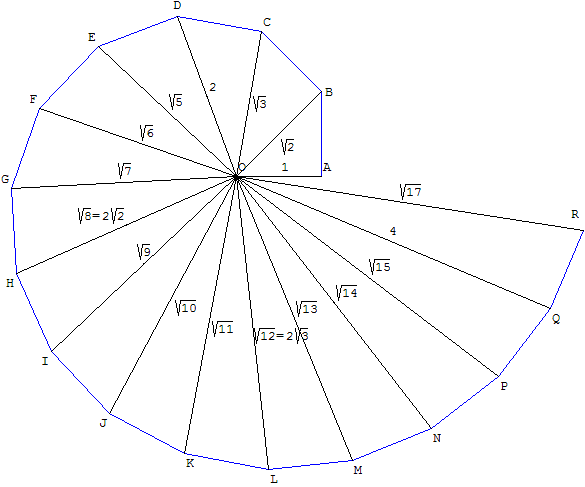
Theodorus Of Cyrene
Theodorus of Cyrene (; 450 BC) was an ancient Greek mathematician. The only first-hand accounts of him that survive are in three of Plato's dialogues: the '' Theaetetus'', the ''Sophist'', and the ''Statesman''. In the first dialogue, he posits a mathematical construction now known as the Spiral of Theodorus. Life Little is known as Theodorus' biography beyond what can be inferred from Plato's dialogues. He was born in the northern African colony of Cyrene, and apparently taught both there and in Athens. He complains of old age in the ''Theaetetus'', the dramatic date of 399 BC of which suggests his period of flourishing to have occurred in the mid-5th century. The text also associates him with the sophist Protagoras, with whom he claims to have studied before turning to geometry. A dubious tradition repeated among ancient biographers like Diogenes Laërtius held that Plato later studied with him in Cyrene, Libya. This eminent mathematician Theodorus was, along with Alcibiades ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyrene, Libya
Cyrene, also sometimes anglicization of names, anglicized as Kyrene, was an ancient Greeks, ancient Greek Greek colonization, colony and ancient Romans, Roman Cities of the Roman Empire, city near present-day Shahhat in northeastern Libya in North Africa. It was part of the Pentapolis (North Africa), Pentapolis, an important group of five cities in the region, and gave the area its classical and early modern name Cyrenaica. Cyrene lies on a ridge of the Jebel Akhdar (Libya), Jebel Akhdar uplands. The archaeological remains cover several hectares and include several monumental temples, stoas, theatres, bathhouses, churches, and palatial residences. The city is surrounded by the Necropolis of Cyrene. Since 1982, it has been a UNESCO World Heritage Site. The city's port was Apollonia, Cyrenaica, Apollonia (Marsa Sousa), located about to the north. The city was attributed to Apollo and the legendary etymology, etymon Cyrene (mythology), Cyrene by the Greeks themselves but it was p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Arithmetic
In mathematics, modular arithmetic is a system of arithmetic operations for integers, other than the usual ones from elementary arithmetic, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book '' Disquisitiones Arithmeticae'', published in 1801. A familiar example of modular arithmetic is the hour hand on a 12-hour clock. If the hour hand points to 7 now, then 8 hours later it will point to 3. Ordinary addition would result in , but 15 reads as 3 on the clock face. This is because the hour hand makes one rotation every 12 hours and the hour number starts over when the hour hand passes 12. We say that 15 is ''congruent'' to 3 modulo 12, written 15 ≡ 3 (mod 12), so that 7 + 8 ≡ 3 (mod 12). Similarly, if one starts at 12 and waits 8 hours, the hour hand will be at 8. If one instead waited twice as long, 16 hours, the hour hand would be on 4. This ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nth Root
In mathematics, an th root of a number is a number which, when raised to the power of , yields : r^n = \underbrace_ = x. The positive integer is called the ''index'' or ''degree'', and the number of which the root is taken is the ''radicand.'' A root of degree 2 is called a ''square root'' and a root of degree 3, a '' cube root''. Roots of higher degree are referred by using ordinal numbers, as in ''fourth root'', ''twentieth root'', etc. The computation of an th root is a root extraction. For example, is a square root of , since , and is also a square root of , since . The th root of is written as \sqrt /math> using the radical symbol \sqrt. The square root is usually written as , with the degree omitted. Taking the th root of a number, for fixed , is the inverse of raising a number to the th power, and can be written as a fractional exponent: \sqrt = x^. For a positive real number , \sqrt denotes the positive square root of and \sqrt /math> denotes the pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scholia
Scholia (: scholium or scholion, from , "comment", "interpretation") are grammatical, critical, or explanatory comments – original or copied from prior commentaries – which are inserted in the margin of the manuscript of ancient authors, as glosses. One who writes scholia is a scholiast. The earliest attested use of the word dates to the 1st century BC. History Ancient scholia are important sources of information about many aspects of the ancient world, especially ancient literary history. The earliest scholia, usually anonymous, date to the 5th or 4th century BC (such as the ''scholia minora'' to the ''Iliad''). The practice of compiling scholia continued to late Byzantine times, outstanding examples being Archbishop Eustathius' massive commentaries to Homer in the 12th century and the ''scholia recentiora'' of Thomas Magister, Demetrius Triclinius and Manuel Moschopoulos in the 14th. Scholia were altered by successive copyists and owners of the manusc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Escargot Pythagore
Snails are eaten by humans in many areas such as Africa, Southeast Asia and Mediterranean Europe, while in other cultures, snails are seen as a taboo food. In English, edible land snails are commonly called escargot, from the French word for 'snail'. Snails as a food date back to ancient times, with numerous cultures worldwide having traditions and practices that attest to their consumption. In the modern era snails are farmed, an industry known as heliciculture. The snails are collected after the rains and are put to "purge" (fasting). In the past, the consumption of snails had a marked seasonality, from April to June. Now, snail-breeding techniques make them available all year. Heliciculture occurs mainly in Spain, France, and Italy, which are also the countries with the greatest culinary tradition of the snail. Although throughout history the snail has had little value in the kitchen because it is considered "poverty food", in recent times it can be classified as a delicacy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpolation
In the mathematics, mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one often has a number of data points, obtained by sampling (statistics), sampling or experimentation, which represent the values of a function for a limited number of values of the Dependent and independent variables, independent variable. It is often required to interpolate; that is, estimate the value of that function for an intermediate value of the independent variable. A closely related problem is the function approximation, approximation of a complicated function by a simple function. Suppose the formula for some given function is known, but too complicated to evaluate efficiently. A few data points from the original function can be interpolated to produce a simpler function which is still fairly close to the original. The resulting gai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philip J
Philip, also Phillip, is a male name derived from the Greek (''Philippos'', lit. "horse-loving" or "fond of horses"), from a compound of (''philos'', "dear", "loved", "loving") and (''hippos'', "horse"). Prominent Philips who popularized the name include kings of Macedonia and one of the apostles of early Christianity. ''Philip'' has many alternative spellings. One derivation often used as a surname is Phillips. The original Greek spelling includes two Ps as seen in Philippides and Philippos, which is possible due to the Greek endings following the two Ps. To end a word with such a double consonant—in Greek or in English—would, however, be incorrect. It has many diminutive (or even hypocoristic) forms including Phil, Philly, Phillie, Lip, and Pip. There are also feminine forms such as Philippine and Philippa. Philip in other languages * Afrikaans: Filip * Albanian: Filip * Amharic: ፊሊጶስ (Filip'os) * Arabic: فيلبس (Fīlibus), فيليبوس ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypotenuse
In geometry, a hypotenuse is the side of a right triangle opposite to the right angle. It is the longest side of any such triangle; the two other shorter sides of such a triangle are called '' catheti'' or ''legs''. Every rectangle can be divided into a pair of right triangles by cutting it along either diagonal; the diagonals are the hypotenuses of these triangles. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two legs. Mathematically, this can be written as a^2 + b^2 = c^2, where ''a'' is the length of one leg, ''b'' is the length of another leg, and ''c'' is the length of the hypotenuse. For example, if one of the legs of a right angle has a length of 3 and the other has a length of 4, then their squares add up to 25 = 9 + 16 = 3 × 3 + 4 × 4. Since 25 is the square of the hypotenuse, the length of the hypotenuse is the square r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees). The side opposite to the right angle is called the '' hypotenuse'' (side c in the figure). The sides adjacent to the right angle are called ''legs'' (or ''catheti'', singular: '' cathetus''). Side a may be identified as the side ''adjacent'' to angle B and ''opposite'' (or ''opposed to'') angle A, while side b is the side adjacent to angle A and opposite angle B. Every right triangle is half of a rectangle which has been divided along its diagonal. When the rectangle is a square, its right-triangular half is isosceles, with two congruent sides and two congruent angles. When the rectangle is not a square, its right-triangular half is scalene. Every triangle whose base is the diameter of a circle and whose apex lies on the circle is a right triangle, with the right angle at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Consequence
Logical consequence (also entailment or logical implication) is a fundamental concept in logic which describes the relationship between statement (logic), statements that hold true when one statement logically ''follows from'' one or more statements. A Validity (logic), valid logical argument is one in which the Consequent, conclusion is entailed by the premises, because the conclusion is the consequence of the premises. The philosophical analysis of logical consequence involves the questions: In what sense does a conclusion follow from its premises? and What does it mean for a conclusion to be a consequence of premises?Beall, JC and Restall, Greg, Logical Consequence' The Stanford Encyclopedia of Philosophy (Fall 2009 Edition), Edward N. Zalta (ed.). All of philosophical logic is meant to provide accounts of the nature of logical consequence and the nature of logical truth. Logical consequence is logical truth, necessary and Formalism (philosophy of mathematics), formal, by wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Continued Fraction
In mathematics, an infinite periodic continued fraction is a simple continued fraction that can be placed in the form : x = a_0 + \cfrac where the initial block [a_0; a_1, \dots, a_k] of ''k''+1 partial denominators is followed by a block [a_, a_, \dots, a_] of ''m'' partial denominators that repeats ''ad infinitum''. For example, \sqrt2 can be expanded to the periodic continued fraction [1; 2, 2, 2, ...]. This article considers only the case of periodic regular continued fractions. In other words, the remainder of this article assumes that all the partial denominators ''a''''i'' (''i'' ≥ 1) are positive integers. The general case, where the partial denominators ''a''''i'' are arbitrary real or complex numbers, is treated in the article convergence problem. Purely periodic and periodic fractions Since all the partial numerators in a regular continued fraction are equal to unity we can adopt a shorthand notation in which the continued fraction shown above is writte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Continued Fraction
A simple or regular continued fraction is a continued fraction with numerators all equal one, and denominators built from a sequence \ of integer numbers. The sequence can be finite or infinite, resulting in a finite (or terminated) continued fraction like :a_0 + \cfrac or an infinite continued fraction like :a_0 + \cfrac Typically, such a continued fraction is obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In the ''finite'' case, the iteration/recursion is stopped after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an ''infinite'' continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers a_i are called the coefficients or terms of the continued fraction. Simple co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |