|
The Symmetries Of Things
''The Symmetries of Things'' is a book on mathematical symmetry and the symmetries of geometric objects, aimed at audiences of multiple levels. It was written over the course of many years by John Horton Conway, Heidi Burgiel, and Chaim Goodman-Strauss, and published in 2008 by A K Peters. Its critical reception was mixed, with some reviewers praising it for its accessible and thorough approach to its material and for its many inspiring illustrations, and others complaining about its inconsistent level of difficulty, overuse of neologisms, failure to adequately cite prior work, and technical errors. Topics ''The Symmetries of Things'' has three major sections, subdivided into 26 chapters. The first of the sections discusses the symmetries of geometric objects. It includes both the symmetries of finite objects in two and three dimensions, and two-dimensional infinite structures such as frieze patterns and tessellations, and develops a new notation for these symmetries based on wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry (geometry)
In geometry, an object has symmetry if there is an operation or transformation (such as translation, scaling, rotation or reflection) that maps the figure/object onto itself (i.e., the object has an invariance under the transform). Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be ''symmetric under rotation'' or to have ''rotational symmetry''. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry. The types of symmetries that are possible for a geometric object depend on the set of geometric transforms available, and on what object properties should remain unchanged after a transformation. Because the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
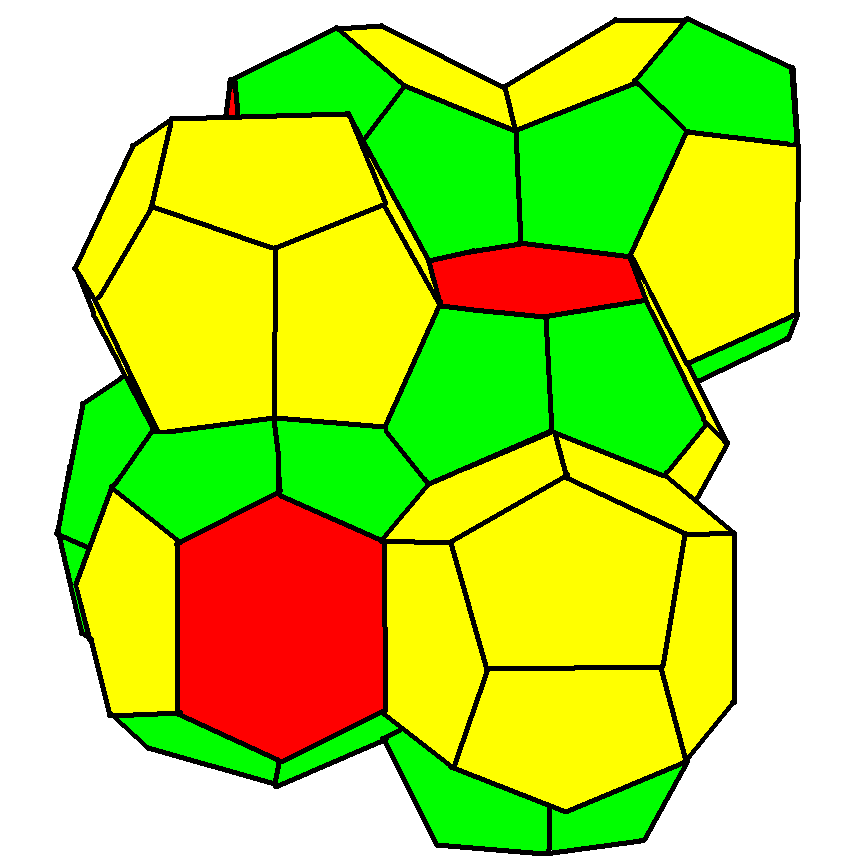
Weaire–Phelan Structure
In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure. History and the Kelvin problem In two dimensions, the subdivision of the plane into cells of equal area with minimum average perimeter is given by the hexagonal tiling, but although the first record of this honeycomb conjecture goes back to the ancient Roman scholar Marcus Terentius Varro, it was not proven until the work of Thomas C. Hales in 1999. In 1887, Lord Kelvin asked the corresponding question for three-dimensional space: how can space be partitioned into cells of equal volume with the least area of surface between them? Or, in short, what was the most efficient soap bubble foam? Thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
11-cell
In mathematics, the 11-cell (or hendecachoron) is a self-dual abstract regular 4-polytope ( four-dimensional polytope). Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. It has Schläfli symbol , with 3 hemi-icosahedra (Schläfli type ) around each edge. It has symmetry order 660, computed as the product of the number of cells (11) and the symmetry of each cell (60). The symmetry structure is the abstract group projective special linear group L2(11). It was discovered in 1977 by Branko Grünbaum, who constructed it by pasting hemi-icosahedra together, three at each edge, until the shape closed up. It was independently discovered by H. S. M. Coxeter in 1984, who studied its structure and symmetry in greater depth. Related polytopes Orthographic projection of 10-simplex with 11 vertices, 55 edges. The abstract ''11-cell'' contains the same number of vertices and edges as the 10-dimensional 10-simplex, and contains 1/3 of its 165 faces. Thus it can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Polytope
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines. A geometric polytope is said to be a ''realization'' of an abstract polytope in some real N-dimensional space, typically Euclidean. This abstract definition allows more general combinatorial structures than traditional definitions of a polytope, thus allowing new objects that have no counterpart in traditional theory. Introductory concepts Traditional versus abstract polytopes In Euclidean geometry, two shapes that are not similar can nonetheless share a common structure. For example a square and a trapezoid both comprise an alternating chain of four vertices and four sides, which makes them quadrilaterals. They are said to be isomorphic or “structure preserving”. This common structure may be represented in an underlying abstract polytope, a purely alg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jaron Lanier
Jaron Zepel Lanier (, born May 3, 1960) is an American computer scientist, visual artist, computer philosophy writer, technologist, futurist, and composer of contemporary classical music. Considered a founder of the field of virtual reality, Lanier and Thomas G. Zimmerman left Atari in 1985 to found VPL Research, Inc., the first company to sell VR goggles and wired gloves. In the late 1990s, Lanier worked on applications for Internet2, and in the 2000s, he was a visiting scholar at Silicon Graphics and various universities. In 2006 he began to work at Microsoft, and from 2009 has worked at Microsoft Research as an Interdisciplinary Scientist. Lanier has composed contemporary classical music and is a collector of rare instruments (of which he owns one to two thousand); his acoustic album, ''Instruments of Change'' (1994) features Asian wind and string instruments such as the khene mouth organ, the suling flute, and the sitar-like esraj. Lanier teamed with Mario Grigor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. One-dimensional manifolds include lines and circles, but not lemniscates. Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions. The concept has applications in computer-graphics given the need to associate pictures with coordinates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grigori Perelman
Grigori Yakovlevich Perelman ( rus, links=no, Григорий Яковлевич Перельман, p=ɡrʲɪˈɡorʲɪj ˈjakəvlʲɪvʲɪtɕ pʲɪrʲɪlʲˈman, a=Ru-Grigori Yakovlevich Perelman.oga; born 13 June 1966) is a Russian mathematician who is known for his contributions to the fields of geometric analysis, Riemannian geometry, and geometric topology. He is widely regarded as one of the greatest living mathematicians. In the 1990s, partly in collaboration with Yuri Burago, Mikhael Gromov, and Anton Petrunin, he made contributions to the study of Alexandrov spaces. In 1994, he proved the soul conjecture in Riemannian geometry, which had been an open problem for the previous 20 years. In 2002 and 2003, he developed new techniques in the analysis of Ricci flow, and proved the Poincaré conjecture and Thurston's geometrization conjecture, the former of which had been a famous open problem in mathematics for the past century. The full details of Perelman's work ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometrization Conjecture
In mathematics, Thurston's geometrization conjecture states that each of certain three-dimensional topological spaces has a unique geometric structure that can be associated with it. It is an analogue of the uniformization theorem for two-dimensional surfaces, which states that every simply connected Riemann surface can be given one of three geometries ( Euclidean, spherical, or hyperbolic). In three dimensions, it is not always possible to assign a single geometry to a whole topological space. Instead, the geometrization conjecture states that every closed 3-manifold can be decomposed in a canonical way into pieces that each have one of eight types of geometric structure. The conjecture was proposed by , and implies several other conjectures, such as the Poincaré conjecture and Thurston's elliptization conjecture. Thurston's hyperbolization theorem implies that Haken manifolds satisfy the geometrization conjecture. Thurston announced a proof in the 1980s and since then sev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Thurston
William Paul Thurston (October 30, 1946August 21, 2012) was an American mathematician. He was a pioneer in the field of low-dimensional topology and was awarded the Fields Medal in 1982 for his contributions to the study of 3-manifolds. Thurston was a professor of mathematics at Princeton University, University of California, Davis, and Cornell University. He was also a director of the Mathematical Sciences Research Institute. Early life and education William Thurston was born in Washington, D.C. to Margaret Thurston (), a seamstress, and Paul Thurston, an aeronautical engineer. William Thurston suffered from congenital strabismus as a child, causing issues with depth perception. His mother worked with him as a toddler to reconstruct three-dimensional images from two-dimensional ones. He received his bachelor's degree from New College in 1967 as part of its inaugural class. For his undergraduate thesis, he developed an intuitionist foundation for topology. Following this, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard K
Richard is a male given name. It originates, via Old French, from Old Frankish and is a compound of the words descending from Proto-Germanic ''*rīk-'' 'ruler, leader, king' and ''*hardu-'' 'strong, brave, hardy', and it therefore means 'strong in rule'. Nicknames include " Richie", "Dick", " Dickon", " Dickie", "Rich", " Rick", " Rico", " Ricky", and more. Richard is a common English, German and French male name. It's also used in many more languages, particularly Germanic, such as Norwegian, Danish, Swedish, Icelandic, and Dutch, as well as other languages including Irish, Scottish, Welsh and Finnish. Richard is cognate with variants of the name in other European languages, such as the Swedish "Rickard", the Catalan "Ricard" and the Italian "Riccardo", among others (see comprehensive variant list below). People named Richard Multiple people with the same name * Richard Andersen (other) * Richard Anderson (other) * Richard Cartwright (disambiguati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons. There are 47 non-prismatic convex uniform 4-polytopes. There are two infinite sets of convex prismatic forms, along with 17 cases arising as prisms of the convex uniform polyhedra. There are also an unknown number of non-convex star forms. History of discovery * Convex Regular polytopes: ** 1852: Ludwig Schläfli proved in his manuscript ''Theorie der vielfachen Kontinuität'' that there are exactly 6 regular polytopes in 4 dimensions and only 3 in 5 or more dimensions. * Regular star 4-polytopes (star polyhedron cells and/or vertex figures) ** 1852: Ludwig Schläfli also found 4 of the 10 regular star 4-polytopes, discounting 6 with cells or vertex figures and . ** 1883: Edmund Hess completed the list of 10 of the nonconvex regular 4-polytopes, in his book (in German) ''Einleitung in die Leh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hearing The Shape Of A Drum
To hear the shape of a drum is to infer information about the shape of the drumhead from the sound it makes, i.e., from the list of overtones, via the use of mathematical theory. "Can One Hear the Shape of a Drum?" is the title of a 1966 article by Mark Kac in the ''American Mathematical Monthly'' which made the question famous, though this particular phrasing originates with Lipman Bers. Similar questions can be traced back all the way to physicist Arthur Schuster in 1882. For his paper, Kac was given the Lester R. Ford Award in 1967 and the Chauvenet Prize in 1968. The frequencies at which a drumhead can vibrate depend on its shape. The Helmholtz equation calculates the frequencies if the shape is known. These frequencies are the eigenvalues of the Laplacian in the space. A central question is whether the shape can be predicted if the frequencies are known; for example, whether a Reuleaux triangle can be recognized in this way. Kac admitted that he did not know whet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |