|
The Book Of Why
''The Book of Why: The New Science of Cause and Effect'' is a 2018 nonfiction book by computer scientist Judea Pearl and writer Dana Mackenzie. The book explores the subject of causality and causal inference from statistical and philosophical points of view for a general audience. Summary The book consists of ten chapters and an introduction. Introduction: Mind over Data The introduction describes the inadequacy of early 20th century statistical methods at making statements about causal relationships between variables. The authors then describe what they term 'The Causal Revolution', which started in the middle of the 20th century, and provided new conceptual and mathematical tools for describing causal relationships. Chapter 1: The Ladder of Causation Chapter 1 introduces the 'ladder of causation' - a diagram used to illustrate the three levels of causal reasoning. The first level is named 'Association', which discusses associations between variables. Questions such as 'is var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Judea Pearl
Judea Pearl (; born September 4, 1936) is an Israeli-American computer scientist and philosopher, best known for championing the probabilistic approach to artificial intelligence and the development of Bayesian networks (see the article on belief propagation). He is also credited for developing a theory of causal and counterfactual inference based on structural models (see article on causality). In 2011, the Association for Computing Machinery (ACM) awarded Pearl with the Turing Award, the highest distinction in computer science, "for fundamental contributions to artificial intelligence through the development of a calculus for probabilistic and causal reasoning". He is the author of several books, including the technical '' Causality: Models, Reasoning and Inference'', and '' The Book of Why'', a book on causality aimed at the general public. Judea Pearl is the father of journalist Daniel Pearl, who was kidnapped and murdered by terrorists in Pakistan connected with Al-Qaeda a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Bayes
Thomas Bayes ( , ; 7 April 1761) was an English statistician, philosopher and Presbyterian minister who is known for formulating a specific case of the theorem that bears his name: Bayes' theorem. Bayes never published what would become his most famous accomplishment; his notes were edited and published posthumously by Richard Price. Biography Thomas Bayes was the son of London Presbyterian minister Joshua Bayes, and was possibly born in Hertfordshire. He came from a prominent Nonconformist (Protestantism), nonconformist family from Sheffield. In 1719, he enrolled at the University of Edinburgh to study logic and theology. On his return around 1722, he assisted his father at the latter's chapel in London before moving to Royal Tunbridge Wells, Tunbridge Wells, Kent, around 1734. There he was minister of the Mount Sion Chapel, until 1752. He is known to have published two works in his lifetime, one theological and one mathematical: #''Divine Benevolence, or an Attempt to P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instrumental Variables
In statistics, econometrics, epidemiology and related disciplines, the method of instrumental variables (IV) is used to estimate causal relationships when controlled experiments are not feasible or when a treatment is not successfully delivered to every unit in a randomized experiment. Intuitively, IVs are used when an explanatory variable of interest is correlated with the error term (endogenous), in which case ordinary least squares and ANOVA give biased results. A valid instrument induces changes in the explanatory variable (is correlated with the endogenous variable) but has no independent effect on the dependent variable and is not correlated with the error term, allowing a researcher to uncover the causal effect of the explanatory variable on the dependent variable. Instrumental variable methods allow for consistent estimation when the explanatory variables (covariates) are correlated with the error terms in a regression model. Such correlation may occur when: # changes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lord's Paradox
In statistics, Lord's paradox raises the issue of when it is appropriate to control for baseline (configuration management), baseline status. In three papers, Frederic M. Lord gave examples when statisticians could reach different conclusions depending on whether they adjust for pre-existing differences.Lord, E. M. (1967). A paradox in the interpretation of group comparisons. Psychological Bulletin, 68, 304–305. Paul W. Holland, Holland & Donald Rubin, Rubin (1983) used these examples to illustrate how there may be multiple valid descriptive comparisons in the data, but causal conclusions require an underlying (untestable) causal model. Judea Pearl used these examples to illustrate how graphical causal models resolve the issue of when control for baseline status is appropriate. Lord's formulation The most famous formulation of Lord's paradox comes from his 1967 paper: ::“A large university is interested in investigating the effects on the students of the diet provided in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Berkson's Paradox
Berkson's paradox, also known as Berkson's bias, collider bias, or Berkson's fallacy, is a result in conditional probability and statistics which is often found to be counterintuitive, and hence a veridical paradox. It is a complicating factor arising in statistical tests of proportions. Specifically, it arises when there is an ascertainment bias inherent in a study design. The effect is related to the explaining away phenomenon in Bayesian networks, and Collider (statistics), conditioning on a collider in graphical models. This paradox is often illustrated using scenarios from the fields of medical statistics or biostatistics, as in the original description of the problem by Joseph Berkson. Examples Overview The most common example of Berkson's paradox is a false observation of a ''negative'' correlation between two desirable traits, i.e., that members of a population which have some desirable traits tend to lack a second. Berkson's paradox occurs when this observation appe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simpson's Paradox
Simpson's paradox is a phenomenon in probability and statistics in which a trend appears in several groups of data but disappears or reverses when the groups are combined. This result is often encountered in social-science and medical-science statistics, and is particularly problematic when frequency data are unduly given causal interpretations. Judea Pearl. ''Causality: Models, Reasoning, and Inference'', Cambridge University Press (2000, 2nd edition 2009). . The paradox can be resolved when confounding variables and causal relations are appropriately addressed in the statistical modeling (e.g., through cluster analysis). Simpson's paradox has been used to illustrate the kind of misleading results that the misuse of statistics can generate. Edward H. Simpson first described this phenomenon in a technical paper in 1951; the statisticians Karl Pearson (in 1899) and Udny Yule (in 1903) had mentioned similar effects earlier. The name ''Simpson's paradox'' was introduced by Col ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monty Hall Problem
The Monty Hall problem is a brain teaser, in the form of a probability puzzle, based nominally on the American television game show ''Let's Make a Deal'' and named after its original host, Monty Hall. The problem was originally posed (and solved) in a letter by Steve Selvin to the ''The American Statistician, American Statistician'' in 1975. It became famous as a question from reader Craig F. Whitaker's letter quoted in Marilyn vos Savant's "Ask Marilyn" column in ''Parade (magazine), Parade'' magazine in 1990: Savant's response was that the contestant should switch to the other door. By the standard assumptions, the switching strategy has a probability of winning the car, while the strategy of keeping the initial choice has only a probability. When the player first makes their choice, there is a chance that the car is behind one of the doors not chosen. This probability does not change after the host reveals a goat behind one of the unchosen doors. When the host provides i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jerome Cornfield
Jerome Cornfield (1912–1979) was an American statistician. He is best known for his work in biostatistics, but his early work was in economic statistics and he was also an early contributor to the theory of Bayesian inference. He played a role in the early development of input-output analysis and linear programming. Cornfield played a crucial role in establishing the causal link between smoking and incidence of lung cancer. He introduced the Rare disease assumption and the "Cornfield condition" that allows one to assess whether an unmeasured (binary) confounder can explain away the observed relative risk due to some exposure like smoking. He was born on October 30, 1912, in The Bronx, New York City. He graduated from New York University in 1933 and was briefly a graduate student at Columbia University. He also studied statistics and mathematics at the Graduate School of the US Department of Agriculture while employed by the Bureau of Labor Statistics, where he remained until ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ronald Fisher
Sir Ronald Aylmer Fisher (17 February 1890 – 29 July 1962) was a British polymath who was active as a mathematician, statistician, biologist, geneticist, and academic. For his work in statistics, he has been described as "a genius who almost single-handedly created the foundations for modern statistical science" and "the single most important figure in 20th century statistics". In genetics, Fisher was the one to most comprehensively combine the ideas of Gregor Mendel and Charles Darwin, as his work used mathematics to combine Mendelian genetics and natural selection; this contributed to the revival of Darwinism in the early 20th-century revision of the theory of evolution known as the Modern synthesis (20th century), modern synthesis. For his contributions to biology, Richard Dawkins declared Fisher to be the greatest of Darwin's successors. He is also considered one of the founding fathers of Neo-Darwinism. According to statistician Jeffrey T. Leek, Fisher is the most in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abraham Lilienfeld
Abraham Morris Lilienfeld (November 13, 1920 – August 6, 1984) was an American epidemiologist and professor at the Johns Hopkins School of Hygiene and Public Health serving in various roles; from lecturer in 1950, he rose to head of the Department of Chronic Diseases in 1961 and chair of the Department of Epidemiology in 1971 before he resigned in 1975. Lilienfeld was known for his work in expanding epidemiology to focus on chronic diseases as well as infectious ones. He also advocated for the link between smoking and lung cancer as early as 1962. The American College of Epidemiology's most prestigious award, the "Abraham Lilienfeld Award", is named in his honour. Early life and education Lilienfeld was born in New York City on November 13, 1920. His father, Joe Lilienfeld, came from a wealthy family in Galicia, Ukraine, and worked as a Galician rabbinical scholar. Joe and his wife had immigrated to the United States in 1914 to escape the draft, leaving their money (which was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
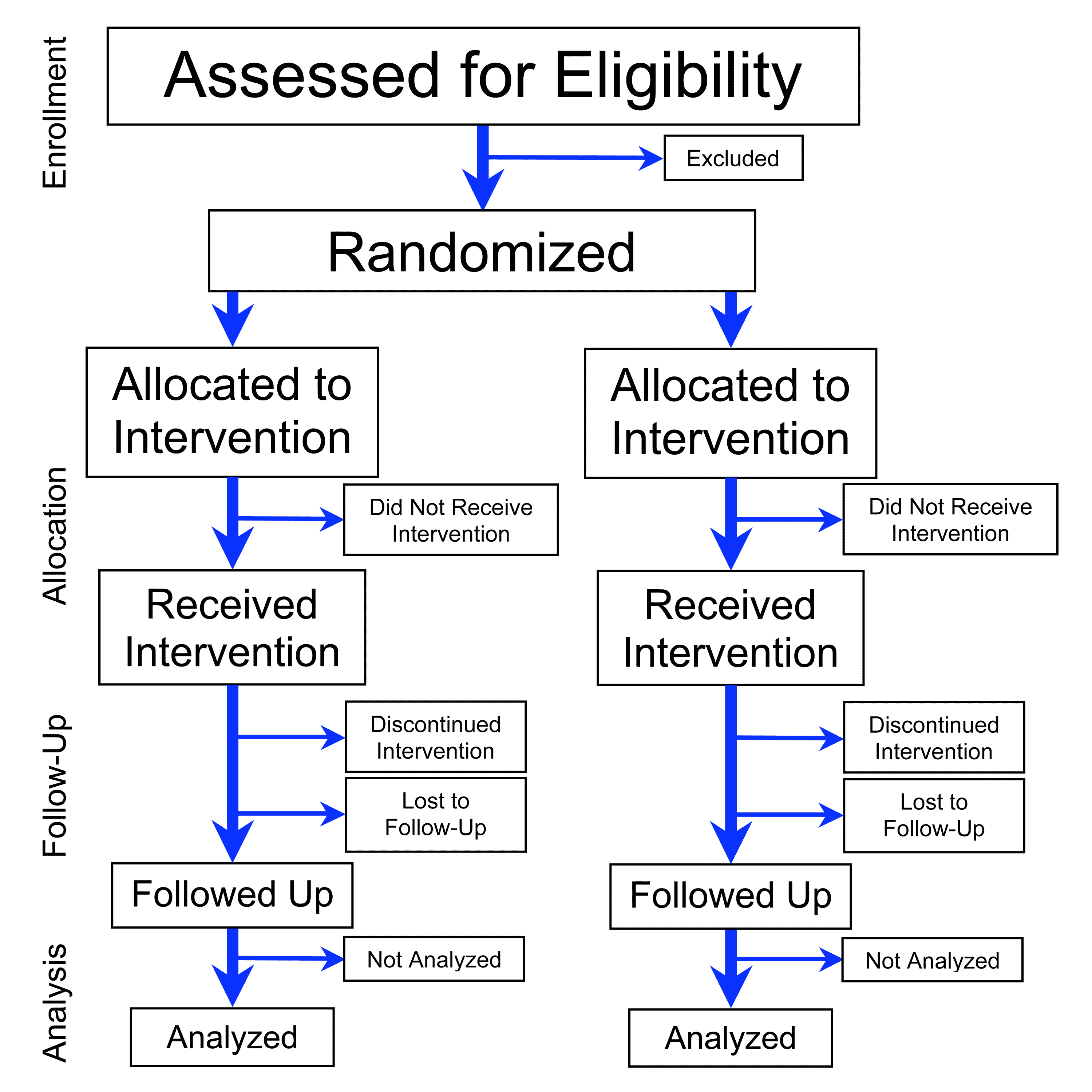
Randomized Controlled Trials
A randomized controlled trial (or randomized control trial; RCT) is a form of scientific experiment used to control factors not under direct experimental control. Examples of RCTs are clinical trials that compare the effects of drugs, surgical techniques, medical devices, diagnostic procedures, diets or other medical treatments. Participants who enroll in RCTs differ from one another in known and unknown ways that can influence study outcomes, and yet cannot be directly controlled. By randomly allocating participants among compared treatments, an RCT enables ''statistical control'' over these influences. Provided it is designed well, conducted properly, and enrolls enough participants, an RCT may achieve sufficient control over these confounding factors to deliver a useful comparison of the treatments studied. Definition and examples An RCT in clinical research typically compares a proposed new treatment against an existing standard of care; these are then termed the 'exper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confounding
In causal inference, a confounder is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations.Pearl, J., (2009). Simpson's Paradox, Confounding, and Collapsibility In ''Causality: Models, Reasoning and Inference'' (2nd ed.). New York : Cambridge University Press. The existence of confounders is an important quantitative explanation why correlation does not imply causation. Some notations are explicitly designed to identify the existence, possible existence, or non-existence of confounders in causal relationships between elements of a system. Confounders are threats to internal validity. Example Let's assume that a trucking company owns a fleet of trucks made by two different manufacturers. Trucks made by one manufacturer are called "A Trucks" and trucks made by the other manufacturer are called "B Trucks." ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |