|
Stella Octangula
The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula (Latin for "eight-pointed star"), a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in Pacioli's ''De Divina Proportione,'' 1509. It is the simplest of five regular polyhedral compounds, and the only regular polyhedral compound composed of only two polyhedra. It can be seen as a 3D extension of the hexagram: the hexagram is a two-dimensional shape formed from two overlapping equilateral triangles, centrally symmetric to each other, and in the same way the stellated octahedron can be formed from two centrally symmetric overlapping tetrahedra. This can be generalized to any desired amount of higher dimensions; the four-dimensional equivalent construction is the compound of two 5-cells. Construction and properties The stellated octahedron is constructed by a stellation of the regular octahedron. In other words, it ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Compound 4 Max
Dual or Duals may refer to: Paired/two things * Dual (mathematics), a notion of paired concepts that mirror one another ** Dual (category theory), a formalization of mathematical duality *** see more cases in :Duality theories * Dual number, a number system used in automatic differentiation * Dual (grammatical number), a grammatical category used in some languages * Dual county, a Gaelic games county which competes in both Gaelic football and hurling * Dual diagnosis, a psychiatric diagnosis of co-occurrence of substance abuse and a mental problem * Dual fertilization, simultaneous application of a P-type and N-type fertilizer * Dual impedance, electrical circuits that are the dual of each other * Dual SIM cellphone supporting use of two SIMs * Aerochute International Dual a two-seat Australian powered parachute design Acronyms and other uses * Dual (brand), a manufacturer of Hifi equipment * DUAL (cognitive architecture), an artificial intelligence design model * DUAL algor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of irregular octahedra also exist, including both convex set, convex and non-convex shapes. Combinatorially equivalent to the regular octahedron The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it: * Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral. * Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Groups In Three Dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group (mathematics), group of all isometry, isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrix, orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries. Symmetry groups of geometric objects are isometry groups. Accordingly, analysis of isometry groups is analysis of possible symmetry, symmetries. All isometries of a Bounded set, bounded (finite) 3D object have one or more common fixed points. We follow the usual convention by choosing the Origin (mathematics), origin as one of them. The symmetry group of an object is sometimes also called its full symmetry group, as opposed to its proper symmetry group, the intersection of its full symmetry group with Euclidean group#Direct and indirect is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Mathematical Gazette
''The Mathematical Gazette'' is a triannual peer-reviewed academic journal published by Cambridge University Press on behalf of the Mathematical Association. It covers mathematics education with a focus on the 15–20 years age range. The journal was established in 1894 by Edward Mann Langley as the successor to the ''Reports of the Association for the Improvement of Geometrical Teaching''. William John Greenstreet was its editor-in-chief for more than thirty years (1897–1930). Since 2000, the editor is Gerry Leversha. Editors-in-chief The following persons are or have been editor-in-chief: Abstracting and indexing The journal is abstracted and indexed in EBSCO databases, Emerging Sources Citation Index, Scopus Scopus is a scientific abstract and citation database, launched by the academic publisher Elsevier as a competitor to older Web of Science in 2004. The ensuing competition between the two databases has been characterized as "intense" and is c ..., and zbMA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Faceting
Stella octangula as a faceting of the cube In geometry, faceting (also spelled facetting) is the process of removing parts of a polygon, polyhedron or polytope, without creating any new Vertex (geometry), vertices. New edges of a faceted polyhedron may be created along face diagonals or internal space diagonals. A ''faceted polyhedron'' will have two faces on each edge and creates new polyhedra or compounds of polyhedra. Faceting is the reciprocal or duality (mathematics), dual process to ''stellation''. For every stellation of some convex polytope, there exists a dual faceting of the dual polytope. Faceted polygons For example, a regular pentagon has one symmetry faceting, the pentagram, and the regular hexagon has two symmetric facetings, one as a polygon, and one as a compound of two triangles. Faceted polyhedra The regular icosahedron can be faceted into three regular Kepler–Poinsot polyhedron, Kepler–Poinsot polyhedra: small stellated dodecahedron, great dodeca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnus Wenninger
Father Magnus J. Wenninger OSB (October 31, 1919Banchoff (2002)– February 17, 2017) was an American mathematician who worked on constructing polyhedron models, and wrote the first book on their construction. Early life and education Born to German immigrants in Park Falls, Wisconsin, Joseph Wenninger always knew he was going to be a priest. From an early age, it was understood that his brother Heinie would take after their father and become a baker, and that Joe, as he was then known, would go into the priesthood. When Wenninger was thirteen, after graduating from the parochial school in Park Falls, Wisconsin, his parents saw an advertisement in the German newspaper ''Der Wanderer'' that would help to shape the rest of his life. The ad was for a preparatory school in Collegeville, Minnesota, associated with the Benedictine St. John's University. While admitting to feeling homesick at first, Wenninger quickly made friends and, after a year, knew that this was where he nee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Two 5-cells
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pentahedroid, tetrahedral pyramid, or 4-simplex (Coxeter's \alpha_4 polytope), the simplest possible convex 4-polytope, and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The 5-cell is a 4-dimensional pyramid with a tetrahedral base and four tetrahedral sides. The regular 5-cell is bounded by five regular tetrahedra, and is one of the six regular convex 4-polytopes (the four-dimensional analogues of the Platonic solids). A regular 5-cell can be constructed from a regular tetrahedron by adding a fifth vertex one edge length distant from all the vertices of the tetrahedron. This cannot be done in 3-dimensional space. The regular 5-cell is a solution to the problem: ''Make 10 equilateral triangles, all of the same size, usin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Symmetry
In geometry, a point reflection (also called a point inversion or central inversion) is a geometric transformation of affine space in which every point (geometry), point is reflected across a designated inversion center, which remains Fixed point (mathematics), fixed. In Euclidean space, Euclidean or pseudo-Euclidean spaces, a point reflection is an isometry (preserves Euclidean distance, distance). In the Euclidean plane, a point reflection is the same as a half turn, half-turn rotation (180° or radians), while in three-dimensional Euclidean space a point reflection is an improper rotation which preserves distances but orientation-reversing, reverses orientation. A point reflection is an involution (mathematics), involution: applying it twice is the identity transformation. An object that is invariant under a point reflection is said to possess point symmetry (also called inversion symmetry or central symmetry). A point group including a point reflection among its symmetrie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
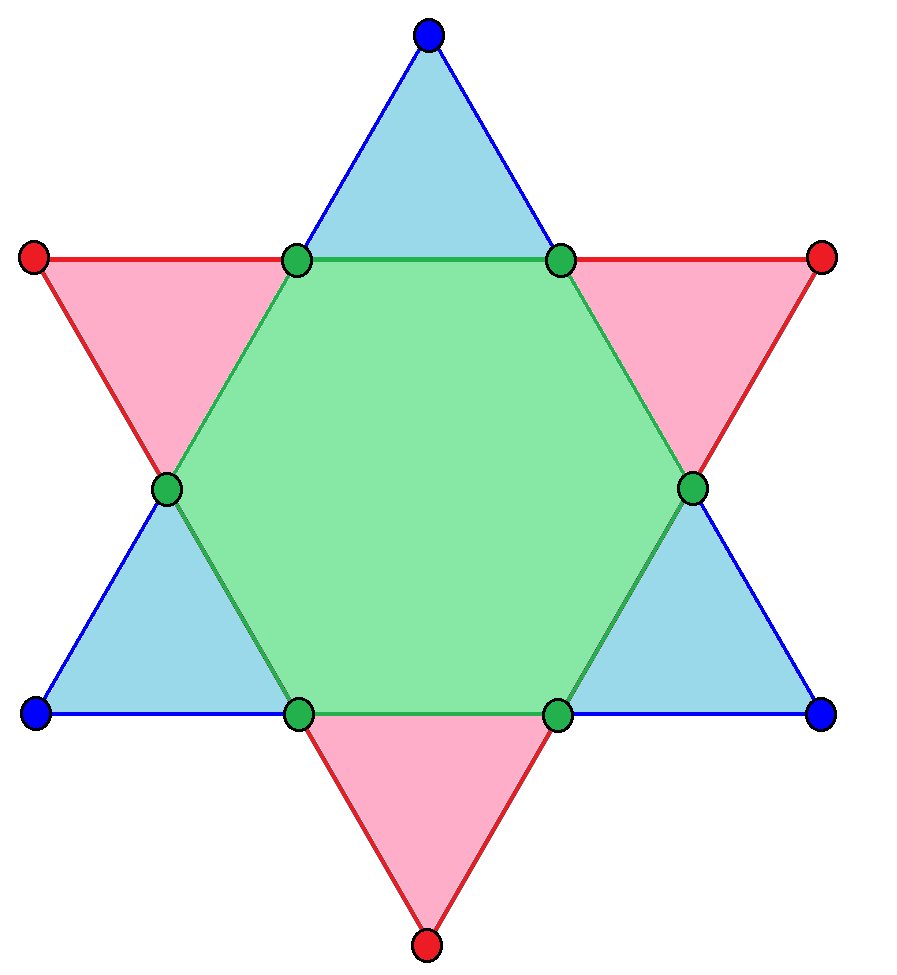
Hexagram
, can be seen as a compound polygon, compound composed of an upwards (blue here) and downwards (pink) facing equilateral triangle, with their intersection as a regular hexagon (in green). A hexagram (Greek language, Greek) or sexagram (Latin language, Latin) is a six-pointed geometric star figure with the Schläfli symbol , 2, or . The term is used to refer to a compound figure of two equilateral triangles. The intersection is a regular hexagon. The hexagram is part of an infinite series of shapes which are compounds of two n-dimensional simplex, simplices. In three dimensions, Compound of two tetrahedra, the analogous compound is the stellated octahedron, and in four dimensions the compound of two 5-cells is obtained. It has been historically used in various religious and cultural contexts and as decorative motifs. The symbol was used as a decorative motif in medieval Christian churches and Jewish synagogues. In the medieval period, a Muslim mystical symbol known as the Seal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedral Compound
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common Centroid, centre. They are the three-dimensional analogs of star polygon#Regular compounds, polygonal compounds such as the hexagram. The outer Vertex (geometry), vertices of a compound can be connected to form a convex polyhedron called its convex hull. A compound is a faceting of its convex hull. Another convex polyhedron is formed by the small central space common to all members of the compound. This polyhedron can be used as the core for a set of stellations. Regular compounds A regular polyhedral compound can be defined as a compound which, like a regular polyhedron, is vertex-transitive, edge-transitive, and face-transitive. Unlike the case of polyhedra, this is not equivalent to the symmetry group acting transitively on its flag (geometry), flags; the compound of two tetrahedra is the only regular compound with that property. There are five regular compounds of polyhe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divina Proportione
''Divina proportione'' (15th century Italian for ''Divine proportion''), later also called ''De divina proportione'' (converting the Italian title into a Latin one) is a book on mathematics written by Luca Pacioli and illustrated by Leonardo da Vinci, completed by February 9th, 1498 in Milan and first printed in 1509. Its subject was mathematical proportions (the title refers to the golden ratio) and their applications to geometry, to visual art through perspective, and to architecture. The clarity of the written material and Leonardo's excellent diagrams helped the book to achieve an impact beyond mathematical circles, popularizing contemporary geometric concepts and images. Some of its content was plagiarised from an earlier book by Piero della Francesca, '' De quinque corporibus regularibus''. Contents of the book The book consists of three separate manuscripts, which Pacioli worked on between 1496 and 1498. He credits Fibonacci as the main source for the mathematics he p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |