|
Statistical Risk
Statistical risk is a quantification of a situation's risk using statistical methods. These methods can be used to estimate a probability distribution for the outcome of a specific variable, or at least one or more key parameters of that distribution, and from that estimated distribution a risk function can be used to obtain a single non-negative number representing a particular conception of the risk of the situation. Statistical risk is taken account of in a variety of contexts including finance and economics, and there are many risk functions that can be used depending on the context. One measure of the statistical risk of a continuous variable, such as the return on an investment, is simply the estimated variance of the variable, or equivalently the square root of the variance, called the standard deviation. Another measure in finance, one which views upside risk as unimportant compared to downside risk, is the downside beta. In the context of a binary variable, a sim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantification (science)
In mathematics and empirical science, quantification (or quantitation) is the act of counting and measuring that maps human sense observations and experiences into quantity, quantities. Quantification in this sense is fundamental to the scientific method. Natural science Some measure of the undisputed general importance of quantification in the natural sciences can be gleaned from the following comments: * "these are mere facts, but they are quantitative facts and the basis of science." * It seems to be held as universally true that "the foundation of quantification is measurement." * There is little doubt that "quantification provided a basis for the objectivity of science." * In ancient times, "musicians and artists ... rejected quantification, but merchants, by definition, quantified their affairs, in order to survive, made them visible on parchment and paper." * Any reasonable "comparison between Aristotle and Galileo shows clearly that there can be no unique lawfulness discov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Upside Risk
In investing, upside risk is the uncertain possibility of gain. It is measured by upside beta. An alternative measure of upside risk is the upper semi-deviation. Upside risk is calculated using data only from days when the benchmark (for example S&P 500 Index) has gone up. Upside risk focuses on uncertain positive returns rather than negative returns. For this reason, upside risk, while a measure of unpredictability of the extent of gains, is not a “risk” in the sense of a possibility of adverse outcomes. Upside risk vs. Capital Asset Pricing Model Looking at upside risk and downside risk separately provides much more useful information to investors than does only looking at the single Capital Asset Pricing Model (CAPM) beta. The comparison of upside to downside risk is necessary because “modern portfolio theory measures risk in terms of standard deviation of asset returns, which treats both positive and negative deviations from expected returns as risk.” In other words, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
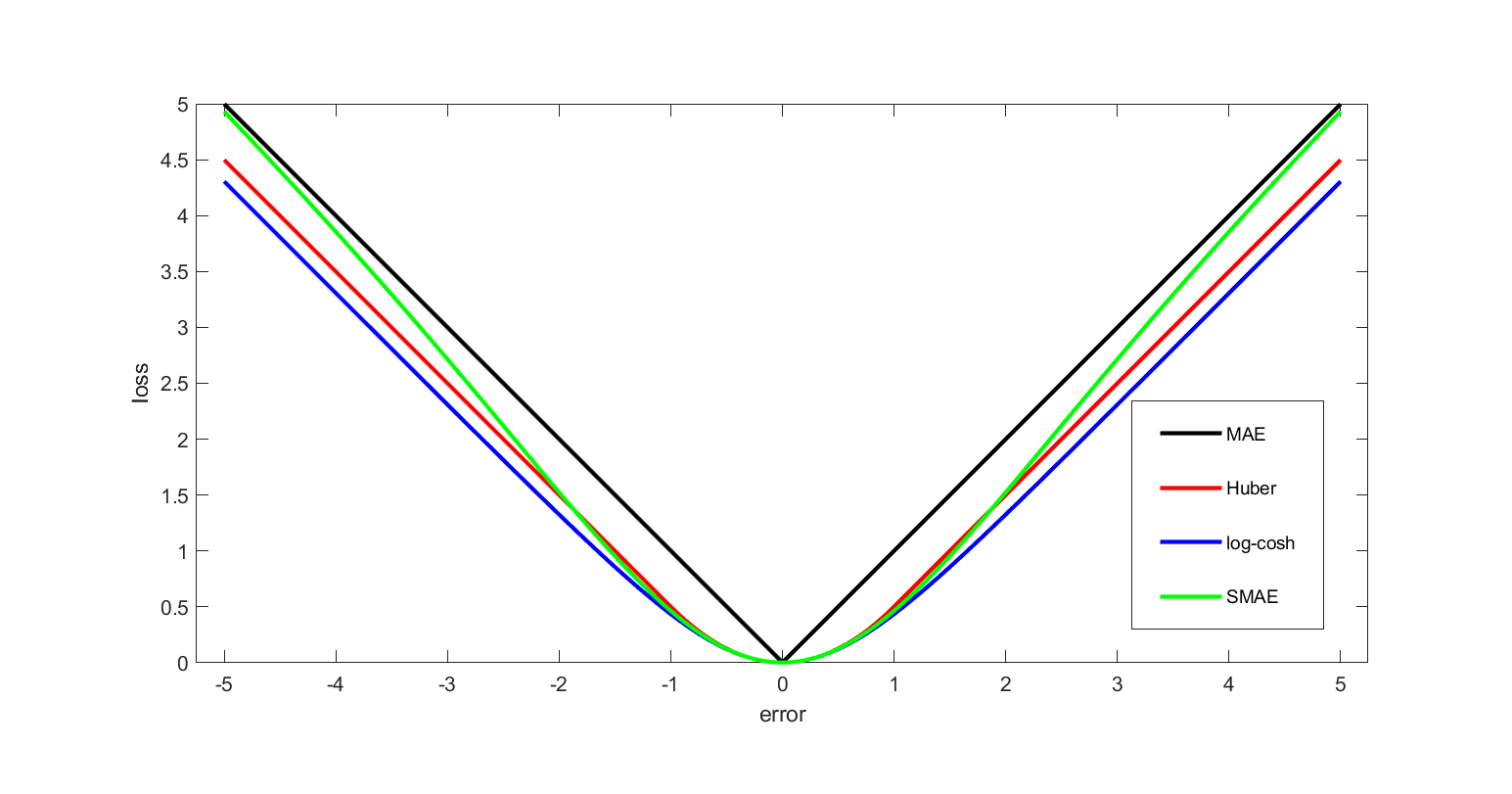
Risk Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economics, for example, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Estimation
Estimation theory is a branch of statistics that deals with estimating the values of parameters based on measured empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the measured data. An ''estimator'' attempts to approximate the unknown parameters using the measurements. In estimation theory, two approaches are generally considered: * The probabilistic approach (described in this article) assumes that the measured data is random with probability distribution dependent on the parameters of interest * The set-membership approach assumes that the measured data vector belongs to a set which depends on the parameter vector. Examples For example, it is desired to estimate the proportion of a population of voters who will vote for a particular candidate. That proportion is the parameter sought; the estimate is based on a small random sample of voters. Alternatively, it is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Ordering
In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word ''partial'' is used to indicate that not every pair of elements needs to be comparable; that is, there may be pairs for which neither element precedes the other. Partial orders thus generalize total orders, in which every pair is comparable. Formally, a partial order is a homogeneous binary relation that is reflexive, antisymmetric, and transitive. A partially ordered set (poset for short) is an ordered pair P=(X,\leq) consisting of a set X (called the ''ground set'' of P) and a partial order \leq on X. When the meaning is clear from context and there is no ambiguity about the partial order, the set X itself is sometimes called a poset. Partial order relations The term ''partial order'' usually refers to the reflexive partial order relations, referred to in this article as ''non-strict'' partial orders. However some a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. More precisely, the PDF is used to specify the probability of the random variable falling ''within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean-preserving Spread
In probability and statistics, a mean-preserving spread (MPS) is a change from one probability distribution A to another probability distribution B, where B is formed by spreading out one or more portions of A's probability density function or probability mass function while leaving the mean (the expected value) unchanged. As such, the concept of mean-preserving spreads provides a stochastic ordering of equal-mean gambles (probability distributions) according to their degree of risk; this ordering is partial, meaning that of two equal-mean gambles, it is not necessarily true that either is a mean-preserving spread of the other. Distribution A is said to be a mean-preserving contraction of B if B is a mean-preserving spread of A. Ranking gambles by mean-preserving spreads is a special case of ranking gambles by second-order stochastic dominance – namely, the special case of equal means: If B is a mean-preserving spread of A, then A is second-order stochastically dominant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an event is to occur."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th ed., (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', vol. 1, 3rd ed., (1968), Wiley, . This number is often expressed as a percentage (%), ranging from 0% to 100%. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written as 0.5 or 50%). These concepts have been given an axiomatic mathematical formaliza ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Variable
Binary data is data whose unit can take on only two possible states. These are often labelled as 0 and 1 in accordance with the binary numeral system and Boolean algebra. Binary data occurs in many different technical and scientific fields, where it can be called by different names including '' bit'' (binary digit) in computer science, ''truth value'' in mathematical logic and related domains and '' binary variable'' in statistics. Mathematical and combinatoric foundations A discrete variable that can take only one state contains zero information, and is the next natural number after 1. That is why the bit, a variable with only two possible values, is a standard primary unit of information. A collection of bits may have states: see binary number for details. Number of states of a collection of discrete variables depends exponentially on the number of variables, and only as a power law on number of states of each variable. Ten bits have more () states than three decimal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Downside Beta
In investing, downside beta is the beta that measures a stock's association with the overall stock market (risk) only on days when the market’s return is negative. Downside beta was first proposed by Roy 1952 and then popularized in an investment book bMarkowitz (1959) Formula It is common to measure r_i and r_m as the excess returns to security i and the market m, u_m as the average market excess return, and Cov and Var as the covariance and variance operators, Downside beta is :\beta^-=\frac, while upside beta is given by this expression with the direction of the inequalities reversed. Therefore, \beta^- can be estimated with a regression of the excess return of security i on the excess return of the market, conditional on (excess) market return being negative. Downside beta vs. beta Downside beta was once hypothesized to have greater explanatory power than standard beta in bearish markets. As such, it would have been a better measure of risk than ordinary beta. Use in Equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Downside Risk
Downside risk is the financial risk associated with losses. That is, it is the risk of the actual return being below the expected return, or the uncertainty about the magnitude of that difference. Risk measures typically quantify the downside risk, whereas the standard deviation (an example of a deviation risk measure) measures both the upside and downside risk. Specifically, downside risk can be measured either with downside beta or by measuring lower semi-deviation. The statistic ''below-target semi-deviation'' or simply ''target semi-deviation'' (TSV) has become the industry standard. History Downside risk was first modeled by Roy (1952), who assumed that an investor's goal was to minimize his/her risk. This mean-semivariance, or downside risk, model is also known as “safety-first” technique, and only looks at the lower standard deviations of expected returns which are the potential losses. This is about the same time Harry Markowitz was developing mean-variance theory. Ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not. Standard deviation may be abbreviated SD or std dev, and is most commonly represented in mathematical texts and equations by the lowercase Greek alphabet, Greek letter Sigma, σ (sigma), for the population standard deviation, or the Latin script, Latin letter ''s'', for the sample standard deviation. The standard deviation of a random variable, Sample (statistics), sample, statistical population, data set, or probability distribution is the square root of its variance. (For a finite population, v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |