|
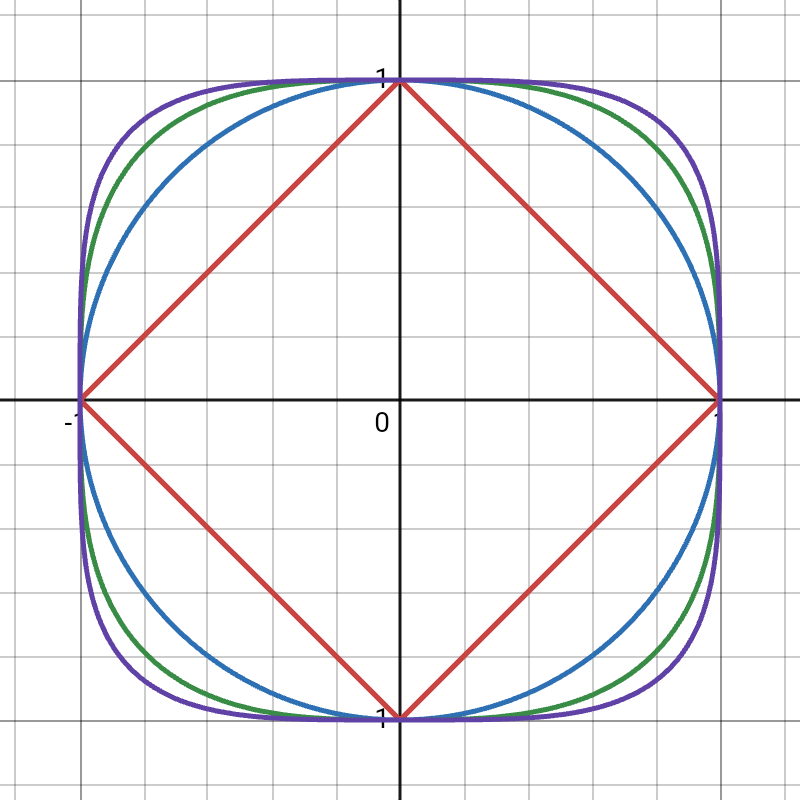
Squigonometry
Squigonometry or -trigonometry is a generalization of traditional trigonometry which replaces the circle and Euclidean distance function with the squircle (shape intermediate between a square and circle) and -norm. While trigonometry deals with the relationships between angles and lengths in the plane using trigonometric functions defined relative to a unit circle, squigonometry focuses on analogous relationships and functions within the context of a unit squircle. Etymology The term squigonometry is a portmanteau of ''square'' or ''squircle'' and ''trigonometry''. It was used by Derek Holton to refer to an analog of trigonometry using a square as a basic shape (instead of a circle) in his 1990 pamphlet ''Creating Problems''. In 2011 it was used by William Wood to refer to trigonometry with a squircle as its base shape in a recreational mathematics article in ''Mathematics Magazine''. In 2016 Robert Poodiack extended Wood's work in another ''Mathematics Magazine'' article. Wood ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superegg
In geometry, a superegg is a solid of revolution obtained by rotating an elongated superellipse with exponent greater than 2 around its longest axis. It is a special case of superellipsoid. Unlike an elongated ellipsoid, an elongated superegg can stand upright on a flat surface, or on top of another superegg. This is due to its curvature being zero at the tips. The shape was popularized by Danish poet and scientist Piet Hein (1905–1996). Supereggs of various materials, including brass, were sold as novelties or " executive toys" in the 1960s. Mathematical description The superegg is a superellipsoid whose horizontal cross-sections are circles. It is defined by the inequality :\left, \frac\^p + \left, \frac\^p \leq 1 \, , where ''R'' is the horizontal radius at the "equator" (the widest part as defined by the circles), and ''h'' is one half of the height. The exponent ''p'' determines the degree of flattening at the tips and equator. Hein's choice was ''p'' = 2.5 (the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lp Space
In mathematics, the spaces are function spaces defined using a natural generalization of the -norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue , although according to the Bourbaki group they were first introduced by Frigyes Riesz . spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, economics, finance, engineering, and other disciplines. Preliminaries The -norm in finite dimensions The Euclidean length of a vector x = (x_1, x_2, \dots, x_n) in the n-dimensional real vector space \Reals^n is given by the Euclidean norm: \, x\, _2 = \left(^2 + ^2 + \dotsb + ^2\right)^. The Euclidean distance between two points x and y is the length \, x - y\, _2 of the straight line b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipsoid
An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional Scaling (geometry), scalings, or more generally, of an affine transformation. An ellipsoid is a quadric surface; that is, a Surface (mathematics), surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is characterized by either of the two following properties. Every planar Cross section (geometry), cross section is either an ellipse, or is empty, or is reduced to a single point (this explains the name, meaning "ellipse-like"). It is Bounded set, bounded, which means that it may be enclosed in a sufficiently large sphere. An ellipsoid has three pairwise perpendicular Rotational symmetry, axes of symmetry which intersect at a Central symmetry, center of symmetry, called the center of the ellipsoid. The line segments that are delimited on the axes of symmetry by the ellipsoid are called the ''principal ax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astroid
In mathematics, an astroid is a particular type of roulette curve: a hypocycloid with four cusp (singularity), cusps. Specifically, it is the Locus (mathematics), locus of a point on a circle as it Rolling, rolls inside a fixed circle with four times the radius. By double generation, it is also the locus of a point on a circle as it rolls inside a fixed circle with 4/3 times the radius. It can also be defined as the Envelope (mathematics), envelope of a line segment of fixed length that moves while keeping an end point on each of the axes. It is therefore the Envelope (mathematics), envelope of the moving bar in the Trammel of Archimedes. Its modern name comes from the Greek word for "star". It was proposed, originally in the form of "Astrois", by Joseph Johann von Littrow in 1838. The curve had a variety of names, including tetracuspid (still used), cubocycloid, and paracycle. It is nearly identical in form to the evolute of an ellipse. Equations If the radius of the fixed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superellipsoid
In mathematics, a superellipsoid (or super-ellipsoid) is a solid geometry, solid whose horizontal sections are superellipses (Lamé curves) with the same squareness parameter \epsilon_2, and whose vertical sections through the center are superellipses with the squareness parameter \epsilon_1. It is a generalization of an ellipsoid, which is a special case when \epsilon_1=\epsilon_2=1. Superellipsoids as computer graphics primitives were popularized by Alan H. Barr (who used the name "superquadrics" to refer to both superellipsoids and supertoroids).Barr, A.H. (1992), ''Rigid Physically Based Superquadrics''. Chapter III.8 of ''Graphics Gems III'', edited by D. Kirk, pp. 137–159 In modern computer vision and robotics literatures, superquadrics and superellipsoids are used interchangeably, since superellipsoids are the most representative and widely utilized shape among all the superquadrics. Superellipsoids have a rich shape vocabulary, including cuboids, cylinders, ellipso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Substitution
In mathematics, a trigonometric substitution replaces a trigonometric function for another expression. In calculus, trigonometric substitutions are a technique for evaluating integrals. In this case, an expression involving a radical function is replaced with a trigonometric one. Trigonometric identities may help simplify the answer. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration. Case I: Integrands containing ''a''2 − ''x''2 Let x = a \sin \theta, and use the identity 1-\sin^2 \theta = \cos^2 \theta. Examples of Case I Example 1 In the integral \int\frac, we may use x=a\sin \theta,\quad dx=a\cos\theta\, d\theta, \quad \theta=\arcsin\frac. Then, \begin \int\frac &= \int\frac \\ pt &= \int\frac \\ pt &= \int\frac \\ pt &= \int d\theta \\ pt &= \theta + C \\ pt &= \arcsin\frac+C. \end The above step requires that a > ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indefinite Integrals
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and . Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval where the function is Riemann integrable is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval. In physics, antiderivatives arise in the context of rectilinear motion (e.g., in explaining the relationship between position, velocity a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strictly Decreasing
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory. In calculus and analysis In calculus, a function f defined on a subset of the real numbers with real values is called ''monotonic'' if it is either entirely non-decreasing, or entirely non-increasing. That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease. A function is termed ''monotonically increasing'' (also ''increasing'' or ''non-decreasing'') if for all x and y such that x \leq y one has f\!\left(x\right) \leq f\!\left(y\right), so f preserves the order (see Figure 1). Likewise, a function is called ''monotonically decreasing'' (also ''decreasing'' or ''non-increasing'') if, whenever x \leq y, then f\!\left(x\right) \geq f\!\left(y\right), so it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Function Rule
In calculus, the inverse function rule is a formula that expresses the derivative of the inverse of a bijective and differentiable function in terms of the derivative of . More precisely, if the inverse of f is denoted as f^, where f^(y) = x if and only if f(x) = y, then the inverse function rule is, in Lagrange's notation, :\left ^\right(y)=\frac. This formula holds in general whenever f is continuous and injective on an interval , with f being differentiable at f^(y)(\in I) and wheref'(f^(y)) \ne 0. The same formula is also equivalent to the expression :\mathcal\left ^\right\frac, where \mathcal denotes the unary derivative operator (on the space of functions) and \circ denotes function composition. Geometrically, a function and inverse function have graphs that are reflections, in the line y=x. This reflection operation turns the gradient of any line into its reciprocal. Assuming that f has an inverse in a neighbourhood of x and that its derivative at that point is non ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ . For a function f\colon X\to Y, its inverse f^\colon Y\to X admits an explicit description: it sends each element y\in Y to the unique element x\in X such that . As an example, consider the real-valued function of a real variable given by . One can think of as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of is the function f^\colon \R\to\R defined by f^(y) = \frac . Definitions Let be a function whose domain is the set , and whose codomain is the set . Then is ''invertible'' if there exists a function from to such that g(f(x))=x for all x\in X and f(g(y))=y for all y\in Y. If is invertible, then there is exactly one functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |