|
Spiral Similarity
Spiral similarity is a plane transformation in mathematics composed of a rotation and a dilation. It is used widely in Euclidean geometry to facilitate the proofs of many theorems and other results in geometry, especially in mathematical competitions and Olympiads. Though the origin of this idea is not known, it was documented in 1967 by Coxeter in his book ''Geometry Revisited''. The following theorem is important for the Euclidian plane: Any two directly similar figures are related either by a translation or by a spiral similarity. ''(Hint: Directly similar figures are similar and have the same orientation)'' Definition A spiral similarity S is composed of a rotation of the plane followed a dilation about a center O with coordinates c in the plane. Expressing the rotation by a linear transformation T(x) and the dilation as multiplying by a scale factor d, a point p gets mapped to S(p) = d(T(p-c))+c. On the complex plane, any spiral similarity can be expressed in the form T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spiral Similarity Example
In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. Helices Two major definitions of "spiral" in the American Heritage Dictionary are:Spiral ''American Heritage Dictionary of the English Language'', Houghton Mifflin Company, Fourth Edition, 2009. # a curve on a plane that winds around a fixed center point at a continuously increasing or decreasing distance from the point. # a three-dimensional curve that turns around an axis at a constant or continuously varying distance while moving parallel to the axis; a . The first definition describes a planar curve, that exten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
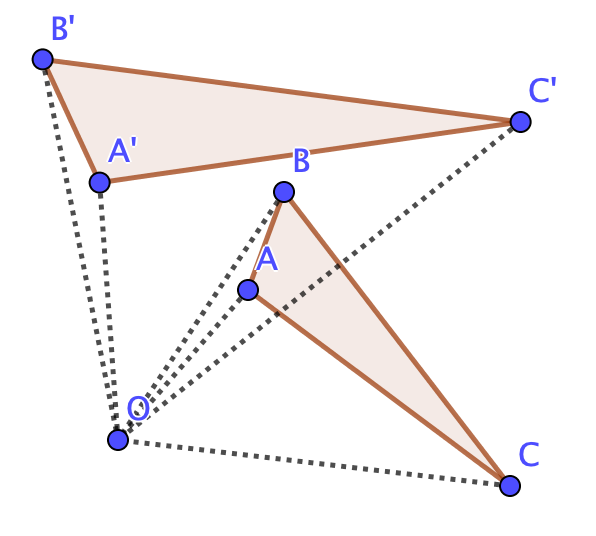
Center Of Spiral Similarity Construction
Center or centre may refer to: Mathematics *Center (geometry), the middle of an object * Center (algebra), used in various contexts ** Center (group theory) ** Center (ring theory) * Graph center, the set of all vertices of minimum eccentricity Places United States * Centre, Alabama * Center, Colorado * Center, Georgia * Center, Indiana * Center, Jay County, Indiana * Center, Warrick County, Indiana * Center, Kentucky * Center, Missouri * Center, Nebraska * Center, North Dakota * Centre County, Pennsylvania * Center, Portland, Oregon * Center, Texas * Center, Washington * Center, Outagamie County, Wisconsin * Center, Rock County, Wisconsin ** Center (community), Wisconsin * Center Township (other) * Centre Township (other) * Centre Avenue (other) * Center Hill (other) Other countries * Centre region, Hainaut, Belgium * Centre Region, Burkina Faso * Centre Region (Cameroon) * Centre-Val de Loire, formerly Centre, France * Centre ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflection Symmetry
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry. In 2D there is a line/axis of symmetry, in 3D a plane of symmetry. An object or figure which is indistinguishable from its transformed image is called mirror symmetric. In conclusion, a line of symmetry splits the shape in half and those halves should be identical. Symmetric function In formal terms, a mathematical object is symmetric with respect to a given operation such as reflection, rotation or translation, if, when applied to the object, this operation preserves some property of the object. The set of operations that preserve a given property of the object form a group. Two objects are symmetric to each other with respect to a given group of operations if one is obtained from the other by some of the operations (and vice versa). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalene Triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of Euclid's Elements. The names used for modern classification are eith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miquel Diagram 1
{{surname ...
Miquel may refer to: * the Catalan form of the given name Michael * Friedrich Anton Wilhelm Miquel (1811–1871), a Dutch botanist * Gérard Miquel (born 1946), a member of the Senate of France * Ignasi Miquel (born 1992), a Spanish football player *Joaquín Miquel (1903–1929), Spanish Olympic runner * Johann von Miquel (1828–1901), a German statesman * Miquel's theorem, a result in geometry, named after Auguste Miquel * Miquel Brown (born 1945), a Canadian actress and disco/soul singer See also *Sant Miquel (other) Sant Miquel (Catalan for Saint Michael) may refer to: Buildings * Sant Miquel, Benedictine monastery in Cruïlles, Monells i Sant Sadurní de l'Heura, Catalonia, Spain *Sant Miquel del Fai, Benedictine monastery in Bigues i Riells, Catalonia, Spain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miquel's Theorem
Miquel's theorem is a result in geometry, named after Auguste Miquel, concerning the intersection of three circles, each drawn through one vertex of a triangle and two points on its adjacent sides. It is one of several results concerning circles in Euclidean geometry due to Miquel, whose work was published in Liouville's newly founded journal '' Journal de mathématiques pures et appliquées''. Formally, let ''ABC'' be a triangle, with arbitrary points ''A´'', ''B´'' and ''C´'' on sides ''BC'', ''AC'', and ''AB'' respectively (or their extensions). Draw three circumcircles (Miquel's circles) to triangles ''AB´C´'', ''A´BC´'', and ''A´B´C''. Miquel's theorem states that these circles intersect in a single point ''M'', called the Miquel point. In addition, the three angles ''MA´B'', ''MB´C'' and ''MC´A'' (green in the diagram) are all equal, as are the three supplementary angles ''MA´C'', ''MB´A'' and ''MC´B''. - Wells refers to Miquel's theorem as the pivot theorem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarity (geometry)
In Euclidean geometry, two objects are similar if they have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (enlarging or reducing), possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other. For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other. If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Correspo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclic Quadrilateral
In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the ''circumcircle'' or ''circumscribed circle'', and the vertices are said to be '' concyclic''. The center of the circle and its radius are called the ''circumcenter'' and the ''circumradius'' respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case. The word cyclic is from the Ancient Greek (''kuklos''), which means "circle" or "wheel". All triangles have a circumcircle, but not all quadrilaterals do. An example of a quadrilateral that cannot be cyclic is a non-square rhombus. The section characterizations below states wha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Translation (geometry)
In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction. A translation can also be interpreted as the addition of a constant vector to every point, or as shifting the origin of the coordinate system. In a Euclidean space, any translation is an isometry. As a function If \mathbf is a fixed vector, known as the ''translation vector'', and \mathbf is the initial position of some object, then the translation function T_ will work as T_(\mathbf)=\mathbf+\mathbf. If T is a translation, then the image of a subset A under the function T is the translate of A by T . The translate of A by T_ is often written A+\mathbf . Horizontal and vertical translations In geometry, a vertical translation (also known as vertical shift) is a translation of a geometric object in a direction parallel to the vertical axis of the Cartesian coordinate system. Often, vertical translatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation
Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional object has an infinite number of possible central axes and rotational directions. If the rotation axis passes internally through the body's own center of mass, then the body is said to be ''autorotating'' or '' spinning'', and the surface intersection of the axis can be called a '' pole''. A rotation around a completely external axis, e.g. the planet Earth around the Sun, is called ''revolving'' or ''orbiting'', typically when it is produced by gravity, and the ends of the rotation axis can be called the '' orbital poles''. Mathematics Mathematically, a rotation is a rigid body movement which, unlike a translation, keeps a point fixed. This definition applies to rotations within both two and three dimensions (in a plane and in spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by the imaginary numbers. The complex plane allows a geometric interpretation of complex numbers. Under addition, they add like vectors. The multiplication of two complex numbers can be expressed more easily in polar coordinates—the magnitude or ''modulus'' of the product is the product of the two absolute values, or moduli, and the angle or ''argument'' of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes known as the Argand plane or Gauss plane. Notational conventions Complex numbers In complex analysis, the complex numbers are customarily represented by the symbol ''z'', which can be separated into its real (''x'') a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |