|
Snub Square Tiling
In geometry, the snub square tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. Its Schläfli symbol is ''s''. Conway calls it a snub quadrille, constructed by a snub operation applied to a square tiling (quadrille). There are 3 regular and 8 semiregular tilings in the plane. Uniform colorings There are two distinct uniform colorings of a snub square tiling. (Naming the colors by indices around a vertex (3.3.4.3.4): 11212, 11213.) Circle packing The snub square tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 5 other circles in the packing ( kissing number).Order in Space: A design source book, Keith Critchlow, p.74-75, circle pattern C : Wythoff construction The snub square tiling can be constructed as a snub operation from the square tiling, or as an alternate truncation from the truncated square tiling. An alte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Kissing Number
In geometry, the kissing number of a mathematical space is defined as the greatest number of non-overlapping unit spheres that can be arranged in that space such that they each touch a common unit sphere. For a given sphere packing (arrangement of spheres) in a given space, a kissing number can also be defined for each individual sphere as the number of spheres it touches. For a Lattice (group), lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another. Other names for kissing number that have been used are Newton number (after the originator of the problem), and contact number. In general, the kissing number problem seeks the maximum possible kissing number for n-sphere, ''n''-dimensional spheres in (''n'' + 1)-dimensional Euclidean space. Ordinary spheres correspond to two-dimensional closed surfaces in three-dimensional space. Finding the kissing number when centers of spheres a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Cairo Pentagonal Tiling
In geometry, a Cairo pentagonal tiling is a tessellation of the Euclidean plane by congruent convex pentagons, formed by overlaying two tessellations of the plane by hexagons and named for its use as a paving design in Cairo. It is also called MacMahon's net after Percy Alexander MacMahon, who depicted it in his 1921 publication ''New Mathematical Pastimes''. John Horton Conway called it a 4-fold pentille. Infinitely many different pentagons can form this pattern, belonging to two of the 15 families of pentagon tiling, convex pentagons that can tile the plane. Their tilings have varying symmetries; all are face-symmetric. One particular form of the tiling, dual to the snub square tiling, has tiles with the minimum possible perimeter among all pentagonal tilings. Another, overlaying two flattened tilings by regular hexagons, is the form used in Cairo and has the property that every edge is collinear with infinitely many other edges. In architecture, beyond Cairo, the Cairo tiling ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Isogonal Tiling
In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in the same or reverse order, and with the same angles between corresponding faces. Technically, one says that for any two vertices there exists a symmetry of the polytope mapping the first isometrically onto the second. Other ways of saying this are that the group of automorphisms of the polytope '' acts transitively'' on its vertices, or that the vertices lie within a single '' symmetry orbit''. All vertices of a finite -dimensional isogonal figure exist on an -sphere. The term isogonal has long been used for polyhedra. Vertex-transitive is a synonym borrowed from modern ideas such as symmetry groups and graph theory. The pseudorhombicuboctahedronwhich is ''not'' isogonaldemonstrates that simply asserting that "all vertices look th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
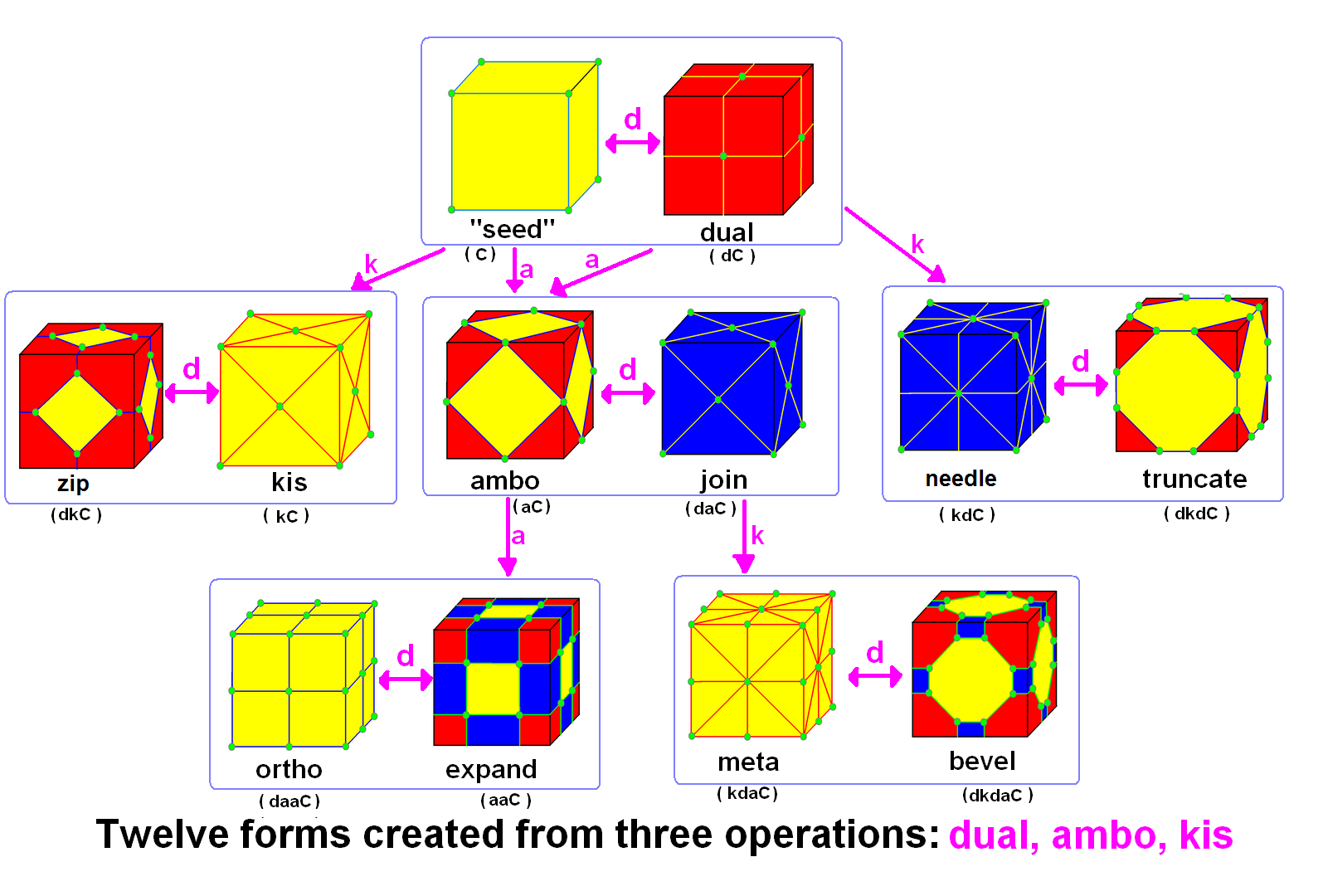 |
Conway Snub Operator
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedron, polyhedra based on a seed polyhedron modified by various prefix operation (mathematics), operations. Conway and Hart extended the idea of using operators, like Truncation (geometry), truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is (topology, topologically) a truncated cuboctahedron. The simplest operator Dual polyhedron, dual swaps Vertex (geometry), vertex and Face (geometry), face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), (Dual polyhedron, dual), (expand), (gyro), (join), (kis), (meta), (ortho), (Snub (geometry), snub), and (Truncation (geometry), truncate), while Hart added (Reflection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Uniform Tiling 44-t012
A uniform is a variety of costume worn by members of an organization while usually participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency services, security guards, in some workplaces and schools, and by inmates in prisons. In some countries, some other officials also wear uniforms in their duties; such is the case of the Commissioned Corps of the United States Public Health Service or the French prefects. For some organizations, such as police, it may be illegal for non-members to wear the uniform. Etymology From the Latin ''unus'' (meaning one), and ''forma'' (meaning form). Variants Corporate and work uniforms Workers sometimes wear uniforms or corporate clothing of one nature or another. Workers required to wear a uniform may include retail workers, bank and post-office workers, public-security and health-care workers, blue-collar employees, personal trainers in he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Dodecagon
In geometry, a dodecagon, or 12-gon, is any twelve-sided polygon. Regular dodecagon A regular polygon, regular dodecagon is a figure with sides of the same length and internal angles of the same size. It has twelve lines of reflective symmetry and rotational symmetry of order 12. A regular dodecagon is represented by the Schläfli symbol and can be constructed as a Truncation (geometry), truncated hexagon, t, or a twice-truncated triangle, tt. The internal angle at each vertex of a regular dodecagon is 150°. Area The area of a regular dodecagon of side length ''a'' is given by: :\begin A & = 3 \cot\left(\frac \right) a^2 = 3 \left(2+\sqrt \right) a^2 \\ & \simeq 11.19615242\,a^2 \end And in terms of the apothem ''r'' (see also inscribed figure), the area is: :\begin A & = 12 \tan\left(\frac\right) r^2 = 12 \left(2-\sqrt \right) r^2 \\ & \simeq 3.2153903\,r^2 \end In terms of the circumradius '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Square (geometry)
In geometry, a square is a regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal sides. As with all rectangles, a square's angles are right angles (90 degrees, or /2 radians), making adjacent sides perpendicular. The area of a square is the side length multiplied by itself, and so in algebra, multiplying a number by itself is called squaring. Equal squares can tile the plane edge-to-edge in the square tiling. Square tilings are ubiquitous in tiled floors and walls, graph paper, image pixels, and game boards. Square shapes are also often seen in building floor plans, origami paper, food servings, in graphic design and heraldry, and in instant photos and fine art. The formula for the area of a square forms the basis of the calculation of area and motivates the search for methods for squaring the circle by compass and straightedge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Octagon
In geometry, an octagon () is an eight-sided polygon or 8-gon. A '' regular octagon'' has Schläfli symbol and can also be constructed as a quasiregular truncated square, t, which alternates two types of edges. A truncated octagon, t is a hexadecagon, . A 3D analog of the octagon can be the rhombicuboctahedron with the triangular faces on it like the replaced edges, if one considers the octagon to be a truncated square. Properties The sum of all the internal angles of any octagon is 1080°. As with all polygons, the external angles total 360°. If squares are constructed all internally or all externally on the sides of an octagon, then the midpoints of the segments connecting the centers of opposite squares form a quadrilateral that is both equidiagonal and orthodiagonal (that is, whose diagonals are equal in length and at right angles to each other).Dao Thanh Oai (2015), "Equilateral triangles and Kiepert perspectors in complex numbers", ''Forum Geometricorum'' 15, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Truncated Square Tiling
In geometry, the truncated square tiling is a semiregular tiling, semiregular tiling by regular polygons of the Euclidean plane with one square (geometry), square and two octagons on each vertex (geometry), vertex. This is the only edge-to-edge tiling by regular polygon, regular convex polygons which contains an octagon. It has Schläfli symbol of ''t''. John Horton Conway, Conway calls it a truncated quadrille, constructed as a truncation (geometry), truncation operation applied to a square tiling (quadrille). Other names used for this pattern include Mediterranean tiling and octagonal tiling, which is often represented by smaller squares, and nonregular octagons which alternate long and short edges. There are 3 List of regular polytopes#Euclidean tilings, regular and 8 List of uniform tilings, semiregular tilings in the plane. Uniform colorings There are two distinct uniform colorings of a truncated square tiling. (Naming the colors by indices around a vertex (4.8.8): 122, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |