|
Sliding Mode Control
In control systems, sliding mode control (SMC) is a nonlinear control method that alters the dynamic system, dynamics of a nonlinear system by applying a discontinuous control signal (or more rigorously, a set-valued control signal) that forces the system to "slide" along a cross-section of the system's normal behavior. The state space (controls), state-feedback control law is not a continuous function of time. Instead, it can switch from one continuous structure to another based on the current position in the state space. Hence, sliding mode control is a variable structure control method. The multiple control structures are designed so that trajectories always move toward an adjacent region with a different control structure, and so the ultimate trajectory will not exist entirely within one control structure. Instead, it will ''slide'' along the boundaries of the control structures. The motion of the system as it slides along these boundaries is called a ''sliding mode'' and the g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Control System
A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial control systems which are used for controlling processes or machines. The control systems are designed via control engineering process. For continuously modulated control, a feedback controller is used to automatically control a process or operation. The control system compares the value or status of the process variable (PV) being controlled with the desired value or setpoint (SP), and applies the difference as a control signal to bring the process variable output of the plant to the same value as the setpoint. For sequential and combinational logic, software logic, such as in a programmable logic controller, is used. Open-loop and closed-loop control Feedback control systems Logic control Logic control systems for indus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Gain (electronics)
In electronics, gain is a measure of the ability of a two-port circuit (often an amplifier) to increase the power or amplitude of a signal from the input to the output port by adding energy converted from some power supply to the signal. It is usually defined as the mean ratio of the signal amplitude or power at the output port to the amplitude or power at the input port. It is often expressed using the logarithmic decibel (dB) units ("dB gain"). A gain greater than one (greater than zero dB), that is, amplification, is the defining property of an active device or circuit, while a passive circuit will have a gain of less than one. The term ''gain'' alone is ambiguous, and can refer to the ratio of output to input voltage (''voltage gain''), current (''current gain'') or electric power (''power gain''). In the field of audio and general purpose amplifiers, especially operational amplifiers, the term usually refers to voltage gain, but in radio frequency amplifiers it usua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Control Systems
A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial control systems which are used for controlling Process (engineering), processes or machines. The control systems are designed via control engineering process. For continuously modulated control, a feedback controller is used to automatically control a process or operation. The control system compares the value or status of the process variable (PV) being controlled with the desired value or Setpoint (control system), setpoint (SP), and applies the difference as a control signal to bring the process variable output of the Plant (control theory), plant to the same value as the setpoint. For Sequential logic, sequential and combinational logic, software logic, such as in a programmable logic controller, is used. Open-loop and closed-loop co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Unique (mathematics)
In mathematics and logic, the term "uniqueness" refers to the property of being the one and only object satisfying a certain condition. This sort of quantification is known as uniqueness quantification or unique existential quantification, and is often denoted with the symbols " ∃!" or "∃=1". It is defined to mean there exists an object with the given property, and all objects with this property are equal. For example, the formal statement : \exists! n \in \mathbb\,(n - 2 = 4) may be read as "there is exactly one natural number n such that n - 2 =4". Proving uniqueness The most common technique to prove the unique existence of an object is to first prove the existence of the entity with the desired condition, and then to prove that any two such entities (say, ''a'' and ''b'') must be equal to each other (i.e. a = b). For example, to show that the equation x + 2 = 5 has exactly one solution, one would first start by establishing that at least one solution exists ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Existence
Existence is the state of having being or reality in contrast to nonexistence and nonbeing. Existence is often contrasted with essence: the essence of an entity is its essential features or qualities, which can be understood even if one does not know whether the entity exists. Ontology is the philosophical discipline studying the nature and types of existence. Singular existence is the existence of individual entities while general existence refers to the existence of concepts or universals. Entities present in space and time have Abstract and concrete, concrete existence in contrast to abstract entities, like numbers and sets. Other distinctions are between Subjunctive possibility, possible, Contingency (philosophy), contingent, and Metaphysical necessity, necessary existence and between Matter, physical and Mind, mental existence. The common view is that an entity either exists or not with nothing in between, but some philosophers say that there are degrees of existence, me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Picard–Lindelöf Theorem
In mathematics, specifically the study of differential equations, the Picard–Lindelöf theorem gives a set of conditions under which an initial value problem has a unique solution. It is also known as Picard's existence theorem, the Cauchy–Lipschitz theorem, or the existence and uniqueness theorem. The theorem is named after Émile Picard, Ernst Lindelöf, Rudolf Lipschitz and Augustin-Louis Cauchy. Theorem Let D \subseteq \R \times \R^n be a closed rectangle with (t_0, y_0) \in \operatorname D, the interior of D. Let f: D \to \R^n be a function that is continuous in t and Lipschitz continuous in y (with Lipschitz constant independent from t). Then there exists some \varepsilon > 0 such that the initial value problem y'(t)=f(t,y(t)),\qquad y(t_0)=y_0 has a unique solution y(t) on the interval _0-\varepsilon, t_0+\varepsilon/math>. Proof sketch A standard proof relies on transforming the differential equation into an integral equation, then applying the Banach fixe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Smooth Function
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives (''differentiability class)'' it has over its domain. A function of class C^k is a function of smoothness at least ; that is, a function of class C^k is a function that has a th derivative that is continuous in its domain. A function of class C^\infty or C^\infty-function (pronounced C-infinity function) is an infinitely differentiable function, that is, a function that has derivatives of all orders (this implies that all these derivatives are continuous). Generally, the term smooth function refers to a C^-function. However, it may also mean "sufficiently differentiable" for the problem under consideration. Differentiability classes Differentiability class is a classification of functions according to the properties of their derivatives. It is a measure of the highest order of derivative that exists and is continuous for a function. Consider an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Column Vector
In linear algebra, a column vector with elements is an m \times 1 matrix consisting of a single column of entries, for example, \boldsymbol = \begin x_1 \\ x_2 \\ \vdots \\ x_m \end. Similarly, a row vector is a 1 \times n matrix for some , consisting of a single row of entries, \boldsymbol a = \begin a_1 & a_2 & \dots & a_n \end. (Throughout this article, boldface is used for both row and column vectors.) The transpose (indicated by ) of any row vector is a column vector, and the transpose of any column vector is a row vector: \begin x_1 \; x_2 \; \dots \; x_m \end^ = \begin x_1 \\ x_2 \\ \vdots \\ x_m \end and \begin x_1 \\ x_2 \\ \vdots \\ x_m \end^ = \begin x_1 \; x_2 \; \dots \; x_m \end. The set of all row vectors with entries in a given field (such as the real numbers) forms an -dimensional vector space; similarly, the set of all column vectors with entries forms an -dimensional vector space. The space of row vectors with entries can be regarded as the dual sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Delta-sigma Modulation
Delta-sigma (ΔΣ; or sigma-delta, ΣΔ) modulation is an oversampling method for encoding signals into low bit depth digital signals at a very high sample-frequency as part of the process of delta-sigma analog-to-digital converters (ADCs) and digital-to-analog converters (DACs). Delta-sigma modulation achieves high quality by utilizing a negative feedback loop during quantization to the lower bit depth that continuously corrects quantization errors and moves quantization noise to higher frequencies well above the original signal's bandwidth. Subsequent low-pass filtering for demodulation easily removes this high frequency noise and time averages to achieve high accuracy in amplitude, which can be ultimately encoded as pulse-code modulation (PCM). Both ADCs and DACs can employ delta-sigma modulation. A delta-sigma ADC (e.g. Figure 1 top) encodes an analog signal using high-frequency delta-sigma modulation and then applies a digital filter to demodulate it t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
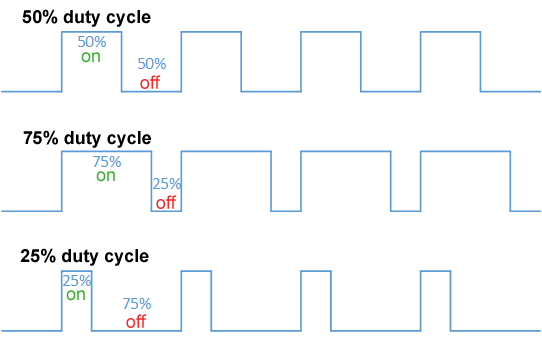 |
Pulse-width Modulation
Pulse-width modulation (PWM), also known as pulse-duration modulation (PDM) or pulse-length modulation (PLM), is any method of representing a signal as a rectangular wave with a varying duty cycle (and for some methods also a varying period). PWM is useful for controlling the average power or amplitude delivered by an electrical signal. The average value of voltage (and current) fed to the load is controlled by switching the supply between 0 and 100% at a rate faster than it takes the load to change significantly. The longer the switch is on, the higher the total power supplied to the load. Along with maximum power point tracking (MPPT), it is one of the primary methods of controlling the output of solar panels to that which can be utilized by a battery. PWM is particularly suited for running inertial loads such as motors, which are not as easily affected by this discrete switching. The goal of PWM is to control a load; however, the PWM switching frequency must be sele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Bang–bang Control
In control theory, a bang–bang controller (hysteresis, 2 step or on–off controller), is a feedback controller that switches abruptly between two states. These controllers may be realized in terms of any element that provides hysteresis. They are often used to control a plant that accepts a binary input, for example a furnace that is either completely on or completely off. Most common residential thermostats are bang–bang controllers. The Heaviside step function in its discrete form is an example of a bang–bang control signal. Due to the discontinuous control signal, systems that include bang–bang controllers are variable structure systems, and bang–bang controllers are thus variable structure controllers. Bang–bang solutions in optimal control In optimal control problems, it is sometimes the case that a control is restricted to be between a lower and an upper bound. If the optimal control switches from one extreme to the other (i.e., is strictly never in between ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |