|
Sierpiński's Constant
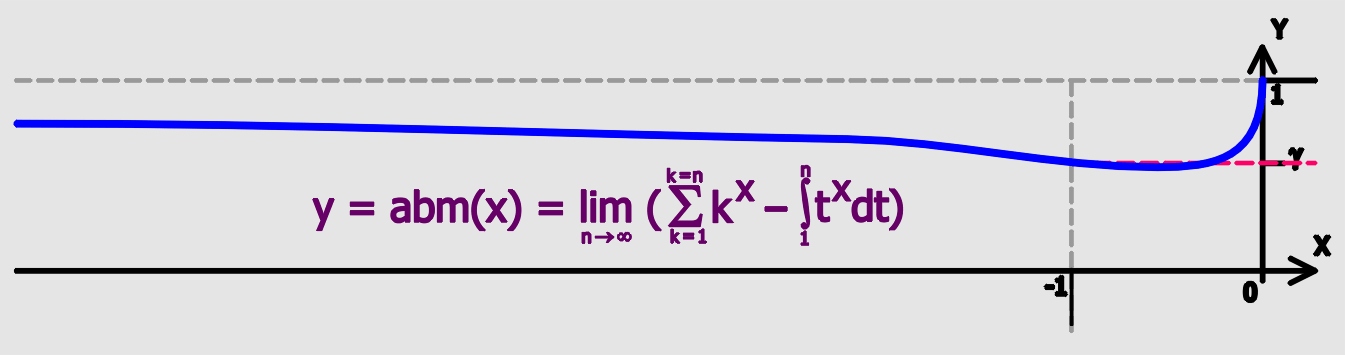
Sierpiński's constant is a mathematical constant usually denoted as ''K''. One way of defining it is as the following limit: :K=\lim_\left sum_^ - \pi\ln n\right/math> where ''r''2(''k'') is a number of representations of ''k'' as a sum of the form ''a''2 + ''b''2 for integer ''a'' and ''b''. It can be given in closed form as: :\begin K &= \pi \left(2 \ln 2+3 \ln \pi + 2 \gamma - 4 \ln \Gamma \left(\tfrac\right)\right)\\ &=\pi \ln\left(\frac\right)\\ &=\pi \ln\left(\frac\right)\\ &= 2.58498 17595 79253 21706 58935 87383\dots \end where \varpi is the lemniscate constant and \gamma is the Euler-Mascheroni constant. Another way to define/understand Sierpiński's constant is, Let r(n) denote the number of representations of n by k squares, then the Summatory Function of r_2(k)/k has the Asymptotic expansion \sum_^=K+\pi\ln n+o\!\left(\frac\right), where K=2.5849817596 is the Sierpinski constant. The above plot shows \left(\sum_^\right)-\pi\ln n, with the value ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Constant
A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a symbol (e.g., an alphabet letter), or by mathematicians' names to facilitate using it across multiple mathematical problems. Constants arise in many areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory, statistics, and calculus. What it means for a constant to arise "naturally", and what makes a constant "interesting", is ultimately a matter of taste, with some mathematical constants being notable more for historical reasons than for their intrinsic mathematical interest. The more popular constants have been studied throughout the ages and computed to many decimal places. All named mathematical constants are definable numbers, and usually are also computable numbers ( Chaitin's constant being a significant exception). Basic mathematical constants These are constants which one is likely to encount ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sum Of Squares Function
In number theory, the sum of squares function is an arithmetic function that gives the number of representations for a given positive integer as the sum of squares, where representations that differ only in the order of the summands or in the signs of the numbers being squared are counted as different, and is denoted by . Definition The function is defined as :r_k(n) = , \, where , \,\ , denotes the cardinality of a set. In other words, is the number of ways can be written as a sum of squares. For example, r_2(1) = 4 since 1 = 0^2 + (\pm 1)^2 = (\pm 1)^2 + 0^2 where each sum has two sign combinations, and also r_2(2) = 4 since 2 = (\pm 1)^2 + (\pm 1)^2 with four sign combinations. On the other hand, r_2(3) = 0 because there is no way to represent 3 as a sum of two squares. Formulae ''k'' = 2 The number of ways to write a natural number as sum of two squares is given by . It is given explicitly by :r_2(n) = 4(d_1(n)-d_3(n)) where is the number of divisors ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemniscate Constant
In mathematics, the lemniscate constant p. 199 is a transcendental mathematical constant that is the ratio of the perimeter of Bernoulli's lemniscate to its diameter, analogous to the definition of for the circle. Equivalently, the perimeter of the lemniscate (x^2+y^2)^2=x^2-y^2 is . The lemniscate constant is closely related to the lemniscate elliptic functions and approximately equal to 2.62205755. The symbol is a cursive variant of ; see Pi § Variant pi. Gauss's constant, denoted by ''G'', is equal to . John Todd named two more lemniscate constants, the ''first lemniscate constant'' and the ''second lemniscate constant'' . Sometimes the quantities or are referred to as ''the'' lemniscate constant. History Gauss's constant G is named after Carl Friedrich Gauss, who calculated it via the arithmetic–geometric mean as 1/M(1,\sqrt). By 1799, Gauss had two proofs of the theorem that M(1,\sqrt)=\pi/\varpi where \varpi is the lemniscate constant. The lemniscate con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler-Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wacław Sierpiński
Wacław Franciszek Sierpiński (; 14 March 1882 – 21 October 1969) was a Polish mathematician. He was known for contributions to set theory (research on the axiom of choice and the continuum hypothesis), number theory, theory of functions, and topology. He published over 700 papers and 50 books. Three well-known fractals are named after him (the Sierpiński triangle, the Sierpiński carpet, and the Sierpiński curve), as are Sierpiński numbers and the associated Sierpiński problem. Educational background Sierpiński enrolled in the Department of Mathematics and Physics at the University of Warsaw in 1899 and graduated four years later. In 1903, while still at the University of Warsaw, the Department of Mathematics and Physics offered a prize for the best essay from a student on Voronoy's contribution to number theory. Sierpiński was awarded a gold medal for his essay, thus laying the foundation for his first major mathematical contribution. Unwilling for his work to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |