|
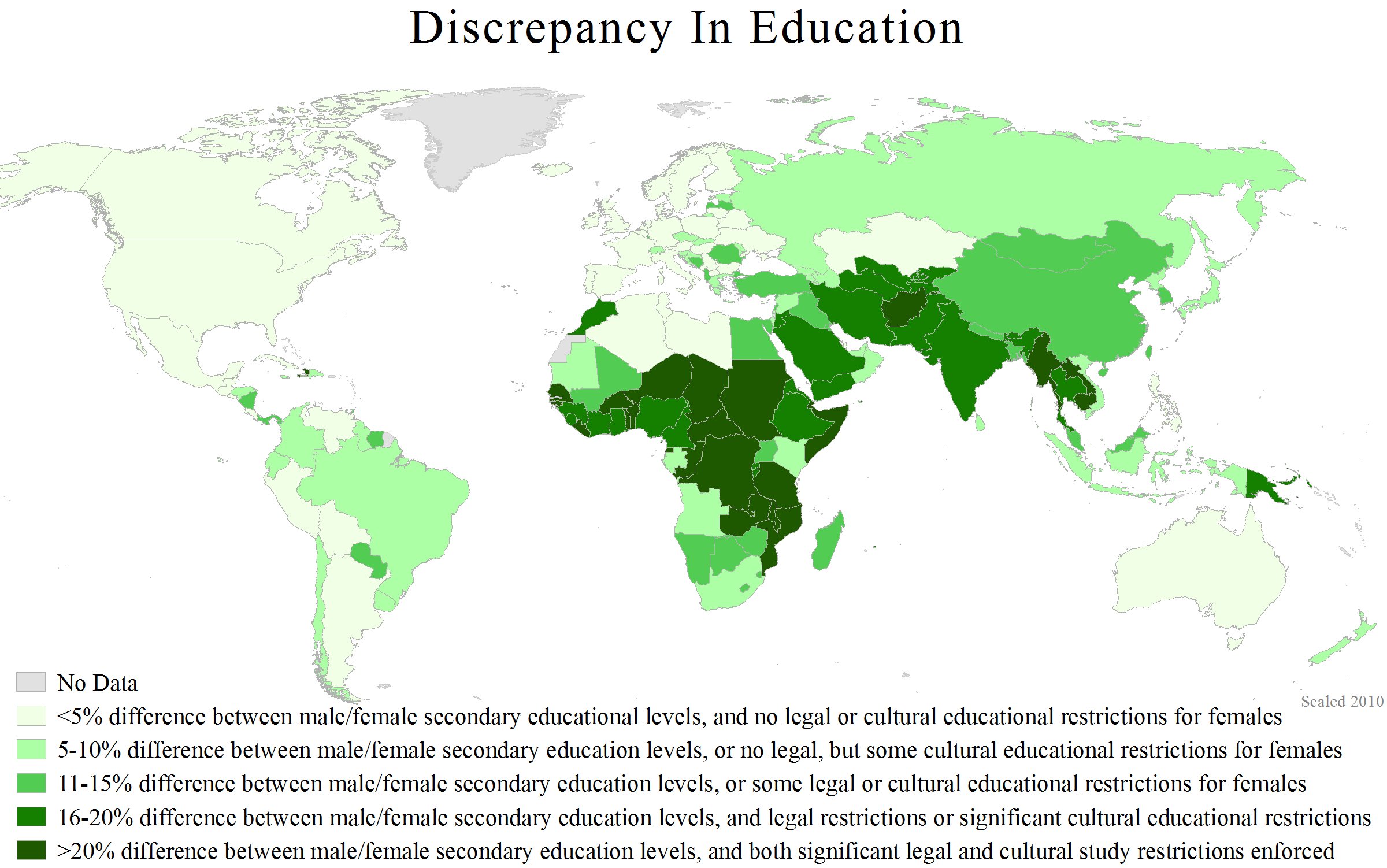
Sexual Dimorphism Measures
Although the subject of sexual dimorphism is not in itself controversial, the measures by which it is assessed differ widely. Most of the measures are used on the assumption that a random variable is considered so that probability distributions should be taken into account. In this review, a series of sexual dimorphism measures are discussed concerning both their definition and the probability law on which they are based. Most of them are sample functions, or statistics, which account for only partial characteristics, for example the mean or expected value, of the distribution involved. Further, the most widely used measure fails to incorporate an inferential support. Introduction It is widely known that sexual dimorphism is an important component of the morphological variation in biological populations (see, e.g., Klein and Cruz-Uribe, 1983; Oxnard, 1987; Kelley, 1993). In higher Primates, sexual dimorphism is also related to some aspects of the social organization and behavior ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sexual Dimorphism
Sexual dimorphism is the condition where the sexes of the same animal and/or plant species exhibit different morphological characteristics, particularly characteristics not directly involved in reproduction. The condition occurs in most animals and some plants. Differences may include secondary sex characteristics, size, weight, colour, markings, or behavioural or cognitive traits. These differences may be subtle or exaggerated and may be subjected to sexual selection and natural selection. The opposite of dimorphism is ''monomorphism'', which is when both biological sexes are phenotypically indistinguishable from each other. Overview Ornamentation and coloration Common and easily identified types of dimorphism consist of ornamentation and coloration, though not always apparent. A difference in coloration of sexes within a given species is called sexual dichromatism, which is commonly seen in many species of birds and reptiles. Sexual selection leads to the exaggerat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be close to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. In a more precise sense, the PDF is used to specify the probability of the random variable falling ''within a particular range of values'', as opposed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gender Differences
Sex differences in humans have been studied in a variety of fields. Sex determination occurs by the presence or absence of a Y in the 23rd pair of chromosomes in the human genome. Phenotypic sex refers to an individual's sex as determined by their internal and external genitalia and expression of secondary sex characteristics. Sex differences generally refer to traits that are sexually dimorphic. A subset of such differences is hypothesized to be the product of the evolutionary process of sexual selection.Mealey, L. (2000). ''Sex differences''. NY: Academic Press. Medicine Sex differences in medicine include sex-specific diseases, which are diseases that occur ''only'' in people of one sex; and sex-related diseases, which are diseases that are more usual to one sex, or which manifest differently in each sex. For example, certain autoimmune diseases may occur predominantly in one sex, for unknown reasons. 90% of primary biliary cirrhosis cases are women, whereas primary sclero ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digit Ratio
The digit ratio is the ratio of the lengths of different digits or fingers on a hand, the study of which has been considered pseudoscience. The 2D:4D ratio is the most studied digit ratio and is calculated by dividing the length of the index finger of a given hand by the length of the ring finger of the same hand. Although studies have claimed to show a correlation between the 2D:4D digit ratio and various physical and behavioral traits, these studies have drawn criticism for irreproducible or contradictory findings, exaggerated claims of usefulness, and lack of high quality research protocols. Measurement The digit length is typically measured on the palmar (ventral, "front", "palm-side") hand, from the midpoint of the bottom crease to the tip of the finger. Measurement of the digits on the dorsal ("back-side") hand, from the tip of the finger to the proximal phalange-bone protrusion (which occurs when digits are bent at 90 degrees to the palm), has recently also gained ac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bateman's Principle
Bateman's principle, in evolutionary biology, is that in most species, variability in reproductive success (or reproductive variance) is greater in males than in females. It was first proposed by Angus John Bateman (1919–1996), an English geneticist. Bateman suggested that, since males are capable of producing millions of sperm cells with little effort, while females invest much higher levels of energy in order to nurture a relatively small number of eggs, the female plays a significantly larger role in their offspring's reproductive success. Bateman's paradigm thus views females as the limiting factor of parental investment, over which males will compete in order to copulate successfully. Although Bateman's principle served as a cornerstone for the study of sexual selection for many decades, it has recently been subject to criticism. Attempts to reproduce Bateman's experiments in 2012 and 2013 were unable to support his conclusions. Some scientists have criticized Bateman' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Null Hypothesis
In scientific research, the null hypothesis (often denoted ''H''0) is the claim that no difference or relationship exists between two sets of data or variables being analyzed. The null hypothesis is that any experimentally observed difference is due to chance alone, and an underlying causative relationship does not exist, hence the term "null". In addition to the null hypothesis, an alternative hypothesis is also developed, which claims that a relationship does exist between two variables. Basic definitions The ''null hypothesis'' and the ''alternative hypothesis'' are types of conjectures used in statistical tests, which are formal methods of reaching conclusions or making decisions on the basis of data. The hypotheses are conjectures about a statistical model of the population, which are based on a sample of the population. The tests are core elements of statistical inference, heavily used in the interpretation of scientific experimental data, to separate scientific claims ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Inference
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the Sequential analysis, dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability". Introduction to Bayes' rule Formal explanation Bayesian inference derives the posterior probability as a consequence relation, consequence of two Antecedent (logic), antecedents: a prior probability and a "likelihood function" derived from a statistical model for the observed data. Bayesian inference computes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain Monte Carlo
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain a sample of the desired distribution by recording states from the chain. The more steps that are included, the more closely the distribution of the sample matches the actual desired distribution. Various algorithms exist for constructing chains, including the Metropolis–Hastings algorithm. Application domains MCMC methods are primarily used for calculating numerical approximations of multi-dimensional integrals, for example in Bayesian statistics, computational physics, computational biology and computational linguistics. In Bayesian statistics, the recent development of MCMC methods has made it possible to compute large hierarchical models that require integrations over hundreds to thousands of unknown parameters. In rare even ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Method Of Moments (statistics)
In statistics, the method of moments is a method of estimation of population parameters. The same principle is used to derive higher moments like skewness and kurtosis. It starts by expressing the population moments (i.e., the expected values of powers of the random variable under consideration) as functions of the parameters of interest. Those expressions are then set equal to the sample moments. The number of such equations is the same as the number of parameters to be estimated. Those equations are then solved for the parameters of interest. The solutions are estimates of those parameters. The method of moments was introduced by Pafnuty Chebyshev in 1887 in the proof of the central limit theorem. The idea of matching empirical moments of a distribution to the population moments dates back at least to Pearson. Method Suppose that the problem is to estimate k unknown parameters \theta_, \theta_2, \dots, \theta_k characterizing the distribution f_W(w; \theta) of the random ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |